回忆一下关于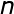 元实值函数的
元实值函数的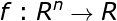 的求导问题,函数
的求导问题,函数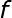 的一阶导数
的一阶导数 为
为
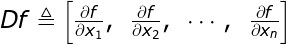
函数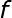 的梯度
的梯度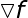 正好是导数
正好是导数 的转置,即
的转置,即%5E%7BT%7D) ;函数
;函数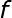 的二阶导数,也称为hessian矩阵,可表示为:
的二阶导数,也称为hessian矩阵,可表示为:
函数
对于向量
这也是一个实值函数,如果
应用链式法则,可得
由此可见,当
一阶必要条件:多元实值函数
成立。
推论:局部极小点位于约束集内部时的一阶必要条件:多元实值函数
成立。
局部极小点的二阶必要条件:多元实值函数
其中,H为函数f的hessian矩阵。
hessian矩阵
局部极小点的二阶充分条件(局部极小点为内点):多元实值函数
1
2
则
-------------------------------------------------------------------------------
转载请注明出处 博客园 刺猬的温驯



 浙公网安备 33010602011771号
浙公网安备 33010602011771号