首先简单描述下快速排序的基本思路

快速排序是基于分治模式处理的，对一个典型子数组A[p...r]排序的分治过程为三个步骤：
1.分解：
A[p..r]被划分为俩个（可能空）的子数组A[p ..q-1]和A[q+1 ..r]，使得
A[p ..q-1] <= A[q] <= A[q+1 ..r]
2.解决：通过递归调用快速排序，对子数组A[p ..q-1]和A[q+1 ..r]排序。
3.合并。

快速排序伪代码(来自算法导论)

 

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16

QUICK_SORT(A,p,r)     if(p<r)         then q <—— PARTITION(A,p,r)              QUICK_SORT(A,p,q-1)              QUICK_SORT(A,q+1,r)   //核心函数，对数组A[p,r]进行就地重排，将小于A[r]的数移到数组前半部分，将大于A[r]的数移到数组后半部分。 PARTITION(A,p,r)     pivot <—— A[r]     i <—— p-1     for j <—— p to r-1         do if A[j] < pivot             i <—— i+1             exchange A[i]<——>A[j]     exchange A[i+1]<——>A[r] return i+1

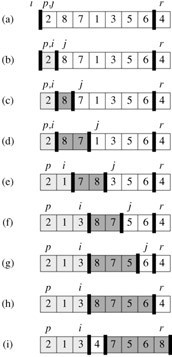
示例：对以下数组，进行快速排序，下图示出了patition过程。

2   8   7   1   3   5   6   4(主元)

 

 

 

 

 

 

 

 

 

一个快速排序的实现代码如下

 

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34

#include <stdio.h> int partition(int *arr,int low,int high) {     int pivot=arr[high];     int i=low-1;     int j,tmp;     for(j=low;j<high;++j)         if(arr[j]<pivot){             tmp=arr[++i];             arr[i]=arr[j];             arr[j]=tmp;         }     tmp=arr[i+1];     arr[i+1]=arr[high];     arr[high]=tmp;     return i+1; } void quick_sort(int *arr,int low,int high) {     if(low<high){         int mid=partition(arr,low,high);         quick_sort(arr,low,mid-1);         quick_sort(arr,mid+1,high);     } } //test int main() {     int arr[10]={1,4,6,2,5,8,7,6,9,12};     quick_sort(arr,0,9);     int i;     for(i=0;i<10;++i)         printf("%d ",arr[i]); }

算法复杂度

最坏情况下的快排时间复杂度：

最坏情况发生在划分过程产生的俩个区域分别包含n-1个元素和一个0元素的时候，
即假设算法每一次递归调用过程中都出现了，这种划分不对称。那么划分的代价为O（n），
因为对一个大小为0的数组递归调用后，返回T（0）=O（1）。
估算法的运行时间可以递归的表示为：

T（n）=T（n-1）+T（0）+O（n)=T(n-1)+O(n).
可以证明为T（n）=O（n^2）。

因此，如果在算法的每一层递归上，划分都是最大程度不对称的，那么算法的运行时间就是O（n^2）。
最快情况下快排时间复杂度：

最快情况下，即PARTITION可能做的最平衡的划分中，得到的每个子问题都不能大于n/2.
因为其中一个子问题的大小为|_n/2_|。另一个子问题的大小为|-n/2-|-1.
在这种情况下，快速排序的速度要快得多：
T(n)<=2T（n/2）+O（n）.可以证得，T（n）=O（nlgn）。

出处：快课   作者：熊大

参考：1.http://blog.csdn.net/v_july_v/article/details/6116297