指派问题与匈牙利解法
指派问题概述:
实际中,会遇到这样的问题,有n项不同的任务,需要n个人分别完成其中的1项,每个人完成任务的时间不一样。于是就有一个问题,如何分配任务使得花费时间最少。
通俗来讲,就是n*n矩阵中,选取n个元素,每行每列各有1个元素,使得和最小。
如下图:
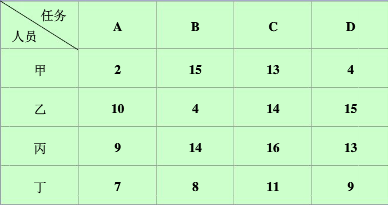
指派问题性质:
指派问题的最优解有这样一个性质,若从矩阵的一行(列)各元素中分别减去该行(列)的最小元素,得到归约矩阵,其最优解和原矩阵的最优解相同.
匈牙利法:

|
12 |
7 |
9 |
7 |
9 |
|
8 |
9 |
6 |
6 |
6 |
|
7 |
17 |
12 |
14 |
9 |
|
15 |
14 |
6 |
6 |
10 |
|
4 |
10 |
7 |
10 |
9 |
1.行归约:
每行元素减去该行的最小元素
|
5 |
0 |
2 |
0 |
2 |
|
2 |
3 |
0 |
0 |
0 |
|
0 |
10 |
5 |
7 |
2 |
|
9 |
8 |
0 |
0 |
4 |
|
0 |
6 |
3 |
6 |
5 |
2.列归约:
每列元素减去该列的最小元素
|
5 |
0 |
2 |
0 |
2 |
|
2 |
3 |
0 |
0 |
0 |
|
0 |
10 |
5 |
7 |
2 |
|
9 |
8 |
0 |
0 |
4 |
|
0 |
6 |
3 |
6 |
5 |
3.试指派:
(1)找到未被画线的含0元素最少的行列,即,遍历所有未被画线的0元素,看下该0元素所在的行列一共有多少个0,最终选取最少个数的那个0元素。
(2)找到该行列中未被画线的0元素,这就是一个独立0元素。对该0元素所在行和列画线。
|
5 |
0 |
2 |
0 |
2 |
|
2 |
3 |
0 |
0 |
0 |
|
0 |
10 |
5 |
7 |
2 |
|
9 |
8 |
0 |
0 |
4 |
|
0 |
6 |
3 |
6 |
5 |
|
5 |
0 |
2 |
0 |
2 |
|
2 |
3 |
0 |
0 |
0 |
|
0 |
10 |
5 |
7 |
2 |
|
9 |
8 |
0 |
0 |
4 |
|
0 |
6 |
3 |
6 |
5 |
|
5 |
0 |
2 |
0 |
2 |
|
2 |
3 |
0 |
0 |
0 |
|
0 |
10 |
5 |
7 |
2 |
|
9 |
8 |
0 |
0 |
4 |
|
0 |
6 |
3 |
6 |
5 |
|
5 |
0 |
2 |
0 |
2 |
|
2 |
3 |
0 |
0 |
0 |
|
0 |
10 |
5 |
7 |
2 |
|
9 |
8 |
0 |
0 |
4 |
|
0 |
6 |
3 |
6 |
5 |
(3)暂时不看被线覆盖的元素,重复(1)(2)直到没有线可以画。
(4)根据(2)找到的0元素个数判断,找到n个独立0元素则Success,小于n个则Fail.(本例子中,n=5,可以看到,第一次试指派之后,独立0元素有4个,不符合)
4.画盖0线:
目标:做最少的直线数覆盖所有0元素,直线数就是独立0元素的个数。
注意:这跟3的线不同;不能用贪心法去画线,比如
1 0 0
1 1 0
1 0 1
若先画横的,则得画3条线,实际只需2条;若先画竖的,将矩阵转置后同理。
步骤3得出的独立0元素的位置
|
5 |
0 |
2 |
0 |
2 |
|
2 |
3 |
0 |
0 |
0 |
|
0 |
10 |
5 |
7 |
2 |
|
9 |
8 |
0 |
0 |
4 |
|
0 |
6 |
3 |
6 |
5 |
(1)对没有独立0元素的行打勾、
(2)对打勾的行所含0元素的列打勾
(3)对所有打勾的列中所含独立0元素的行打勾
(4)重复(2)(3)直到没有不能再打勾
(5)对打勾的列和没有打勾的行画画线,这就是最小盖0线。
|
5 |
0 |
2 |
0 |
2 |
|
|
2 |
3 |
0 |
0 |
0 |
|
|
0 |
10 |
5 |
7 |
2 |
√ |
|
9 |
8 |
0 |
0 |
4 |
|
|
0 |
6 |
3 |
6 |
5 |
√ |
|
√ |
|
5 |
0 |
2 |
0 |
2 |
|
|
2 |
3 |
0 |
0 |
0 |
|
|
0 |
10 |
5 |
7 |
2 |
√ |
|
9 |
8 |
0 |
0 |
4 |
|
|
0 |
6 |
3 |
6 |
5 |
√ |
|
√ |
5.更新矩阵:
(1)对没有被线划到的数中,找到最小的数。
(2)对没有被线划到的数中,减去最小的数。
(3)对被2条线划到的数中,加上最小的数。
|
7 |
0 |
2 |
0 |
2 |
|
4 |
3 |
0 |
0 |
0 |
|
0 |
8 |
3 |
5 |
0 |
|
11 |
8 |
0 |
0 |
4 |
|
0 |
4 |
1 |
4 |
3 |
6.重复3-5直到成功。
|
0 |
1 |
0 |
0 |
0 |
|
0 |
0 |
1 |
0 |
0 |
|
0 |
0 |
0 |
0 |
1 |
|
0 |
0 |
0 |
1 |
0 |
|
1 |
0 |
0 |
0 |
0 |
sum = 7+6+9+6+4 = 32
练习:http://soj.me/show_problem.php?pid=1002&cid=1085
注意题目是求最大值,所以需要对矩阵做一点处理。
代码:

#include <iostream> #include <algorithm> #include <cstring> #include <climits> using namespace std; #define Max 17 int n; //维数 int s[Max][Max]; //原始矩阵 int p[Max][Max]; //归约矩阵 int q[Max][Max]; //0:未被画线 1:画了1次 2: 画了2次(交点) int row[Max], col[Max]; //行列0元素个数 int r[Max][Max]; //0:非0元素 1:非独立0元素 2:独立0元素 int x[Max],y[Max]; //画线时是否被打勾,1是0不是 //数每行每列的0元素个数 void countZero() { memset(row, 0, sizeof(row)); memset(col, 0, sizeof(col)); memset(r, 0, sizeof(r)); for (int i = 0; i < n; ++i) { for (int j = 0; j < n; ++j) { if (p[i][j] == 0) row[i]++, col[j]++; } } } //画最少的线覆盖所有0元素 int drawLine() { memset(q, 0, sizeof(q)); for (int i = 0; i < n; ++i) x[i] = 1, y[i] = 0; //row 对所有不含独立0元素的行打勾! for (int i = 0; i < n; ++i) { for (int j = 0; j < n; ++j) { if (r[i][j] == 2) { x[i] = 0; break; } } } bool is = 1; while (is) //循环直到没有勾可以打 { is = 0; //col 对打勾的行中含0元素的未打勾的列打勾 for (int i = 0; i < n; ++i) { if (x[i] == 1) { for (int j = 0; j < n; ++j) { if (p[i][j] == 0 && y[j] == 0) { y[j] = 1; is = 1; } } } } //row 对打勾的列中含独立0元素的未打勾的行打勾 for (int j = 0; j < n; ++j) { if (y[j] == 1) { for (int i = 0; i < n; ++i) { if (p[i][j] == 0 && x[i] == 0 && r[i][j] == 2) { x[i] = 1; is = 1; } } } } } //没有打勾的行和有打勾的列画线,这就是覆盖所有0元素的最少直线数 int line = 0; for (int i = 0; i < n; ++i) { if (x[i] == 0) { for (int j = 0; j < n; ++j) q[i][j]++; line++; } if (y[i] == 1) { for (int j = 0; j < n; ++j) q[j][i]++; line++; } } return line; } //找独立0元素个数 /*1.找含0最少的那一行/列 2.划掉,更新该行/列0元素所在位置的row[],col[] 3.直到所有0被划线,这里定义为row[]col[]全为INT_MAX,表示该行/列无0元素*/ int find() { countZero(); int zero = 0; //独立0元素的个数 while (1) { //row[i] = INT_MAX表示该行无0元素,防止与*min_element()冲突 for (int i = 0; i < n; ++i) { if (row[i] == 0) row[i] = INT_MAX; if (col[i] == 0) col[i] = INT_MAX; } bool stop = 1; if (*min_element(row, row+n) <= *min_element(col, col+n)) //行最少0元素 { //找含0最少的那一行 int tmp = INT_MAX, index = -1; for (int i = 0; i < n; ++i) { if (tmp > row[i]) tmp = row[i], index = i; } /*找该行任意一个没被划掉的0元素(独立0元素),找到一个就行*/ int index2 = -1; //该行独立0元素的列值 for (int i = 0; i < n; ++i) if (p[index][i] == 0 && col[i] != INT_MAX) { index2 = i; stop = 0; //找到独立0元素则继续循环 zero++; //独立0元素的个数 break; } //找不到独立0元素了 if (stop) break; //标记 row[index] = col[index2] = INT_MAX; r[index][index2] = 1; //独立0元素,等等会++. //更新其所在行列的col,row for (int i = 0; i < n; ++i) if (p[index][i] == 0 && col[i] != INT_MAX) //若该行还有0且没被划掉才更新 col[i]--; for (int i = 0; i < n; ++i) if (p[i][index2] == 0 && row[i] != INT_MAX) row[i]--; } else //列最少0元素 { int tmp = INT_MAX, index = -1; for (int i = 0; i < n; ++i) { if (tmp > col[i]) tmp = col[i], index = i; } int index2 = -1; for (int i = 0; i < n; ++i) if (p[i][index] == 0 && row[i] != INT_MAX) { index2 = i; stop = 0; zero++; break; } if (stop) break; row[index2] = col[index] = INT_MAX; r[index2][index] = 1; for (int i = 0; i < n; ++i) if (p[index2][i] == 0 && col[i] != INT_MAX) col[i]--; for (int i = 0; i < n; ++i) if (p[i][index] == 0 && row[i] != INT_MAX) row[i]--; } } //r[i][j] 0:非0元素 1:非独立0元素 2:独立0元素 for (int i = 0; i < n; ++i) for (int j = 0; j < n; ++j) if (p[i][j] == 0) r[i][j]++; return zero; } int main() { int m; cin >> m; while (m--) { cin >> n; for (int i = 0; i < n; ++i) for (int j = 0; j < n; ++j) cin >> s[i][j]; //行归约 for (int i = 0; i < n; ++i) for (int j = 0; j < n; ++j) p[i][j] = *max_element(s[i], s[i]+n)-s[i][j]; //求和最大 //p[i][j] = s[i][j]-*min_element(s[i],s[i]+j); //求和最小 //列归约 for (int j = 0; j < n; ++j) { int tmp = INT_MAX; for (int i = 0; i < n; ++i) { if (tmp > p[i][j]) tmp = p[i][j]; } for (int i = 0; i < n; ++i) p[i][j] -= tmp; } while (find() < n) { drawLine(); //最小的未被划线的数 int min = INT_MAX; for (int i = 0; i < n; ++i) for (int j = 0; j < n; ++j) if (q[i][j] == 0 && min > p[i][j]) min = p[i][j]; //更新未被划到的和交点 for (int i = 0; i < n; ++i) for (int j = 0; j < n; ++j) if (q[i][j] == 0) p[i][j] -= min; else if (q[i][j] == 2) p[i][j] += min; } //求和 int ans = 0; for (int i = 0; i < n; ++i) for (int j = 0; j < n; ++j) if (r[i][j] == 2) ans += s[i][j]; cout << ans << endl; } }





