《机器学习》第二次作业——第四章学习记录和心得

第四章线性判别与回归

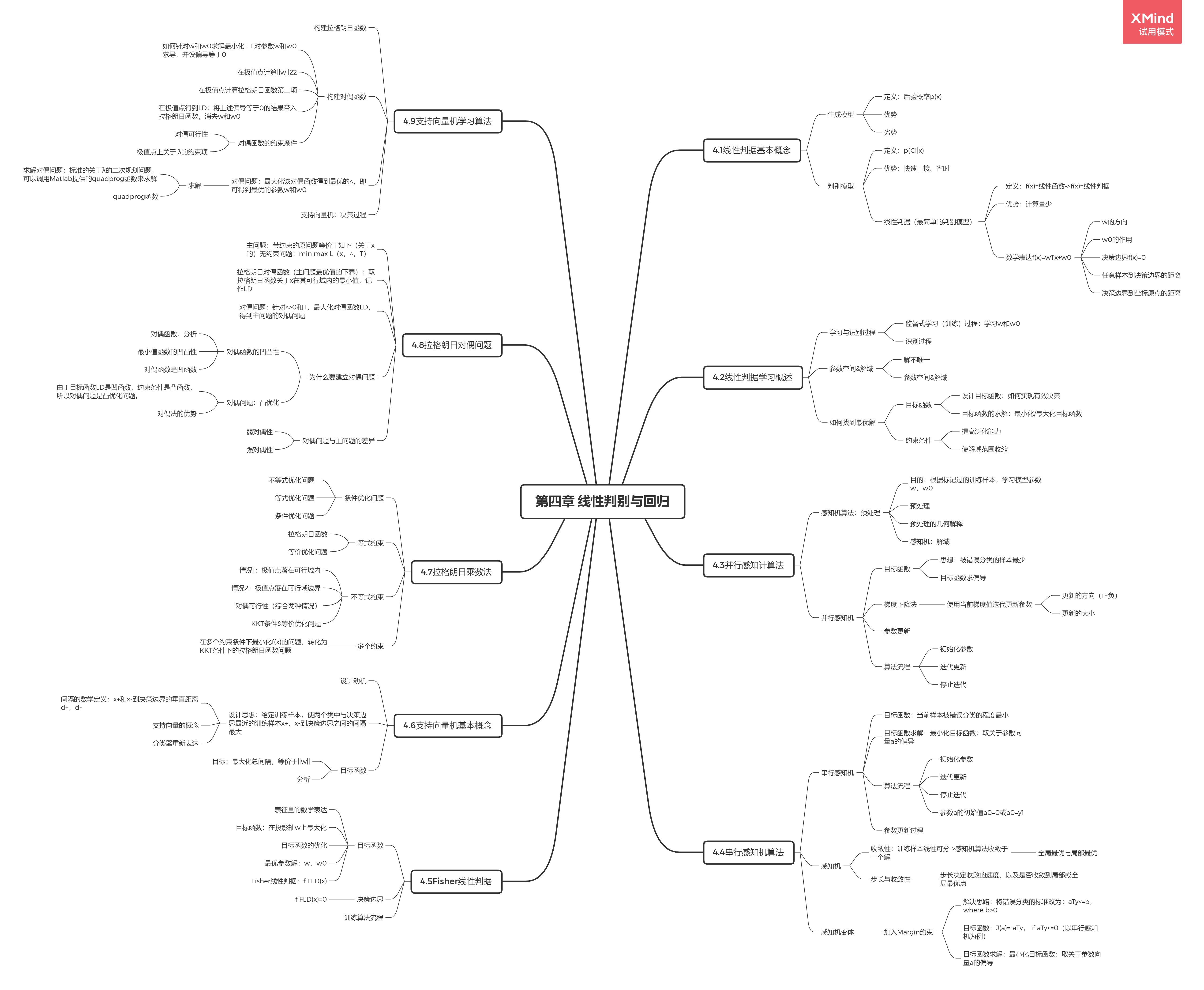
4.1线性判据基本概念

判别模型:给定训练样本xn,直接在输入空间内估计后验概率p(Ci|x)。
优势: 快速直接、省去了耗时的高维观测似然概率估计。
线性判据——最简单的判别模型

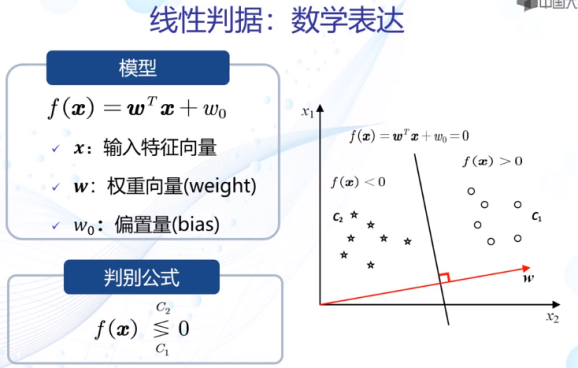
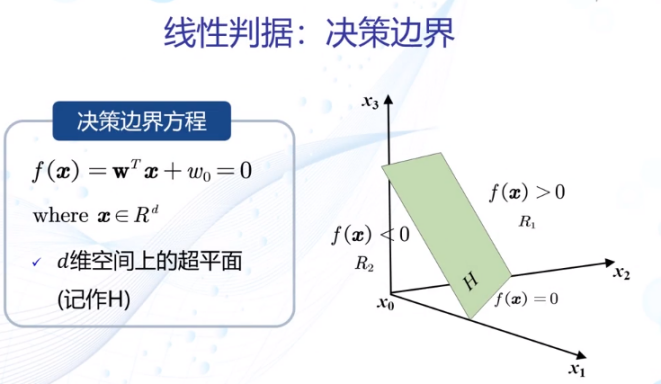
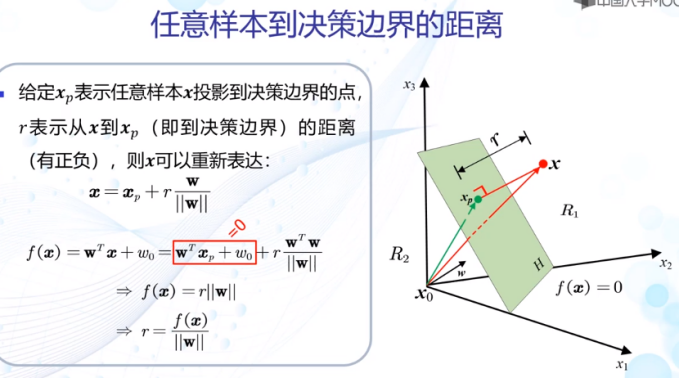
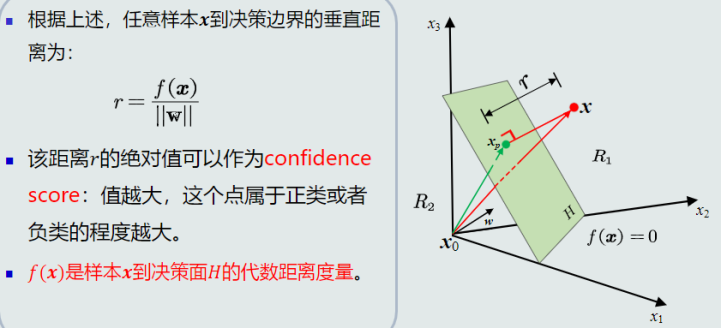
4.2线性判据学习概述

1）设计目标函数

2）最大(小)化目标函数——优化技术、解析求解（求偏导（=0））、迭代求解

3）加入约束条件提高泛化能力

4.3并行感知机算法

• 预处理
  
  
  目标函数求偏导的方法在感知机里不可行——梯度下降法求解
  
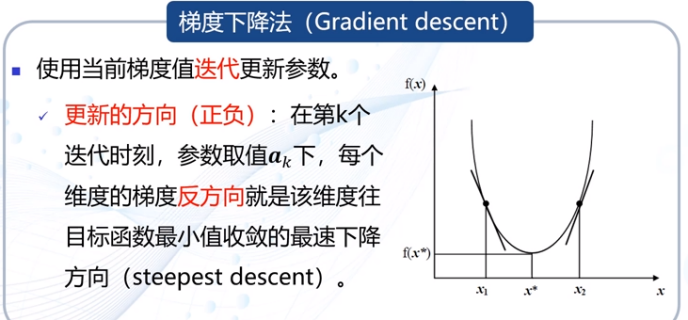
  梯度下降法核心思想：迭代更新。
  加入步长：加快更新的速度。
  

4.4串行感知机算法

• 适合情况: 训练样本是一个个串行给出的。

• 目标函数的求解：同样使用梯度下降法求解
  

• 收敛性:如果训练样本是线性可分的，感知机(并行和串行)算法理论上收敛于一个解。

• 提升感知机的泛化能力：
  
  

4.5Fisher线性判据

1）基本原理：Fisher判据试图找到一个最合适的投影轴，使两个样本在该轴上的重叠部分最少，从而使分类效果达到最佳。

2）投影后：类间差异程度越大越好（均值之差度量），

类内离散程度越小越好（协方差矩阵表征）。

类间散度 Sb=(μ1−μ2)(μ1−μ2)T
类内散度Sw=N1Σ1+N2Σ2

3）目标函数

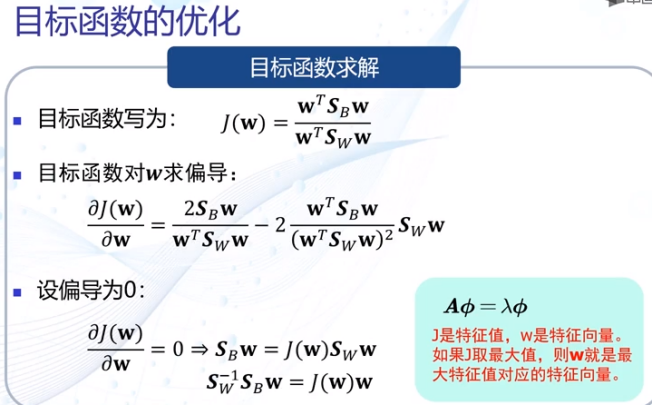
4.6支持向量机基本概念

1）设计思想: 给定一组训练样本，使得两个类中与决策边界最近的训练样本到决策边界之间的间隔最大。

2）间隔计算

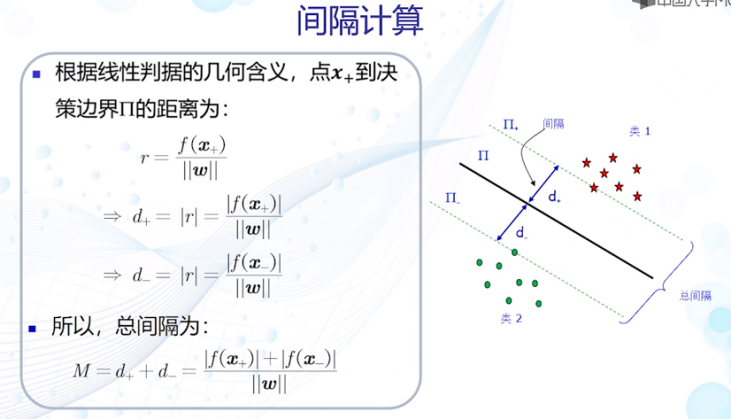
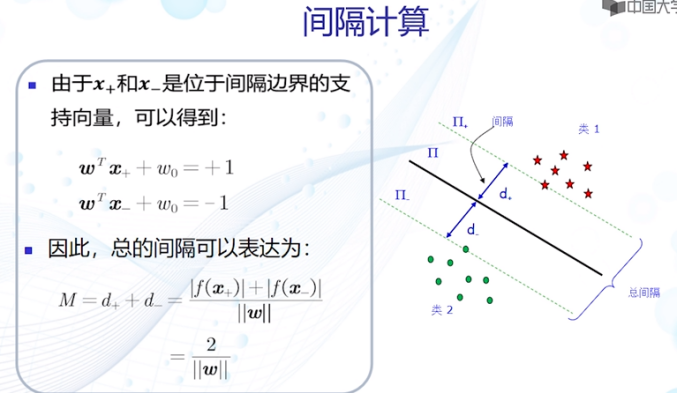
3）目标函数

求解——拉格朗日乘数法

4.7拉格朗日乘数法

求解条件优化问题：1）等式约束优化问题2）不等式约束优化问题



对于不等式约束，拉格朗日函数仍带有约束条件，如何优化求解?——拉格朗日对偶函数

4.8拉格朗日对偶问题

• 对偶问题给出了主问题最优值的下界
  
• 对偶问题与主问题的差异：
  
  

4.9支持向量机学习算法——使用拉格朗日对偶法求解支持向量机

1、构造拉格朗日函数

2、构造对偶函数

4.10软间隔支持向量机——引入软间隔，避免过拟合。

求解目标函数：与硬间隔SVM类似——构建目标函数->构建拉格朗日函数->构建对偶函数(在极值点得到对偶函数LD)

4.11线性判据多类分类

1.多类分类的本质：非线性

2.实现非线性分类的途径：

• 一个模型：能刻化非线性的决策边界。
• 多个模型：多个模型（线性/非线性）组合成非线性决策边界。
• 组合方式：并行组合、串行组合。

思路一：One-to-all

1）假设条件：假设每个类与剩余类可分，总共需要训练K个分类器。
2）问题：每个分类器的正负类样本个数不均衡。
3）混淆区域问题：拒绝选项&重叠。

思路二：线性机

1）假设条件：每个类与剩余类线性可分。
2）训练：基于one-to-all策略训练
3）决策：使用输出值投票法（max函数）——给定测试样本取输出值最大：该值最大表示属于该类的可能性越大。
4）线性机=K个线性模型+一个max函数
    5）线性机的优势：由于使用max函数，不再有混淆区域（即拒绝区域和重叠区域）。通过划定相邻两类之间的边界，分割了重叠区域和拒绝区域。
    6）问题：线性机的前提：每个类与剩余类都线性可分

思路三：one-to-one策略

    1）基本思想：针对每两个类训练一个线性分类器;总共需要训练K(K -1)/2个分类器。
    2)优势：适用于一些线性不可分的情况，从而实现非线性分类；与one-to-all策略相比，不再有重叠区域。
    3)问题：会出现拒绝选项，即样本不属于任何类的情况。

4.12线性回归

目标优化过程：展开目标函数->对参数w求偏导->目标优化（梯度下降法）->最小二乘法

4.13逻辑回归的概念

如果两个类别数据分布的协方差矩阵不同,则MAP分类器的决策边界是一个超二次型曲面，即非线性。
如果两个类别数据分布的协方差矩阵相同，则MAP分类器的决策边界是一个超平面，即线性。

1)MAP分类器等同于一个线性判据，可见，MAP分类器可以在线性和非线性之间切换,为我们将线性模型改进成非线性模型提供了思路。

2)Sigmoid函数：连接线性模型和后验概率的桥梁

3)线性模型 f(x)+Sigmoid函数=后验概率

4)逻辑回归：线性模型 f(x)+Sigmoid函数

决策边界：单个逻辑回归可以用于二类分类；给定两个类，逻辑回归的决策边界仍然是线性的超平面。

5)逻辑回归总结：

逻辑回归本身是一个非线性模型。
逻辑回归用于分类：仍然只能处理两个类别线性可分的情况。但是，sigmoid函数输出了后验概率，使得逻辑回归成为一个非线性模型。因此，逻辑回归比线性模型向前迈进了一步。
逻辑回归用于拟合：可以拟合有限的非线性曲线。

4.14逻辑回归的学习

1）给定训练样本，学习参数w和w。

2）最大似然估计法：给定单个输入样本x，模型输出的类别标签

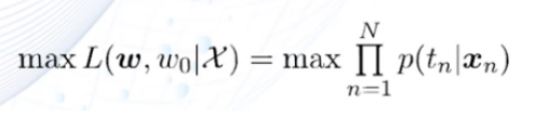
3）目标函数：

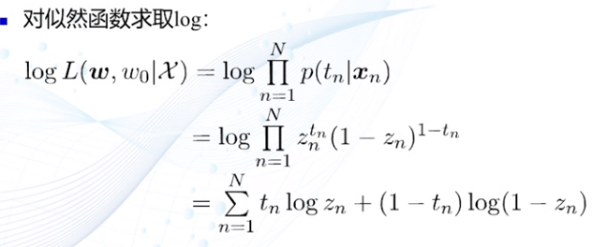
4）交叉熵：交叉熵可以用来度量两种分布的差异程度。

二者一样！

5）目标函数优化：梯度下降法；

步骤：对参数w求偏导；对参数w0求偏导；参数更新：采用梯度下降法更新w和w0;

梯度消失问题

• 当y=wTx+w0较大时，sigmoid函数输出z会出现饱和:输入变化量△y很大时，输出变化量△z很小。
• 在饱和区，输出量z接近于1，导致sigmoid函数梯度值接近于0，出现梯度消失问题。

过拟合问题

• 如果迭代停止条件设为训练误差为0，或者所有训练样本都正确分类的时候才停止，则会出现过拟合问题。
• 所以，在达到一定训练精度后，提前停止迭代，可以避免过拟合。

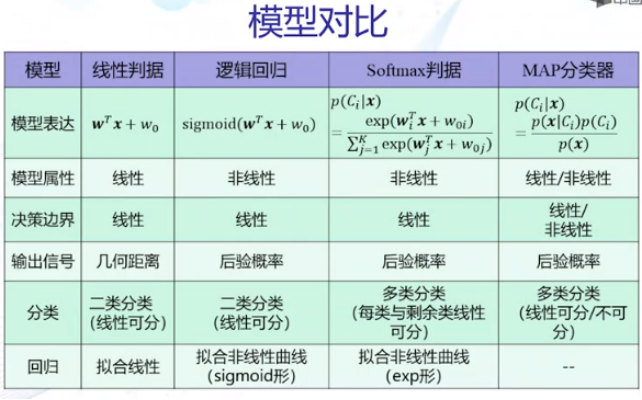
4.15Softmax判据的概念

1）逻辑回归输出:属于正类的后验概率

2）后验概率的多类情况:一个类与剩余类的后验概率比率。逻辑回归是由Logit变换反推出来的。

3）由Logit变换可知:正负类后验概率比率的对数是一个线性函数。

4）分类K个类，可以构建K个线性判据。第i个线性判据表示Ci类与剩余类的分类边界，剩余类用一个参考负类(reference class)CK来表达。

5）对于多类分类，K个线性模型也跟每个类对应的后验概率建立起了联系。

6）Softmax判据:K个线性判据+ softmax函数。

7）Softmax判据用于分类，等同于基于one-to-all策略的线性机。

8）Softmax适用范围：

①分类（前提:每个类和剩余类之间是线性可分的。）
②回归（范围:可以拟合指数函数(exp)形式的非线性曲线。）

4.16Softmax判据的学习

学什么:给定训练样本，学习K组参数

目标函数∶最大似然估计。

针对所有训练样本，最大化输出标签分布的似然函数，以此求得参数的最优值。似然函数为所有训练样本输出概率的乘积。

判别式学习是依赖所有类的训练样本来学习参数。

Softmax:针对每个输出类别分别计算梯度值，但每个参数的梯度值与所有类别样本都相关。

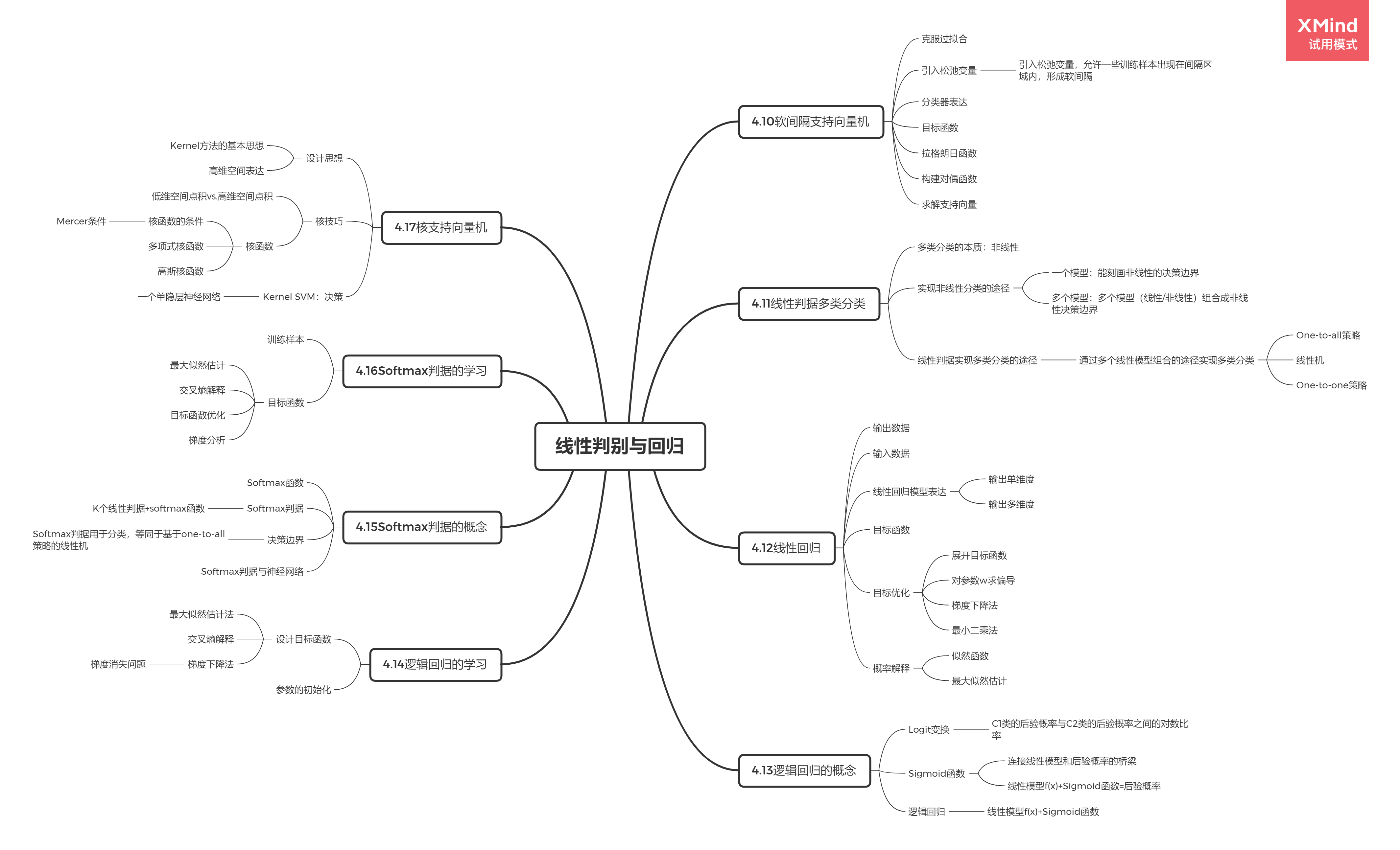
4.17 核支持向量机

1.Kernel方法的基本思想:

如果样本在原始特征空间(X空间)线性不可分，可以将这些样本通过一个函数p映射到一个高维的特征空间(空间)，使得在这个高维空间，这些样本拥有一个线性分类边界。

2.核函数:

在低维X空间的一个非线性函数，包含向量映射和点积功能，即作为X空间两个向量的度量，来表达映射到高维空间的向量之间的点积。

3.Kernel SVM的决策是关于测试样本x与Ns个支持向量xk的核函数的线性组合，即Ns个非线性函数的线性组合。

4.常见核函数

• 多项式核函数:
  

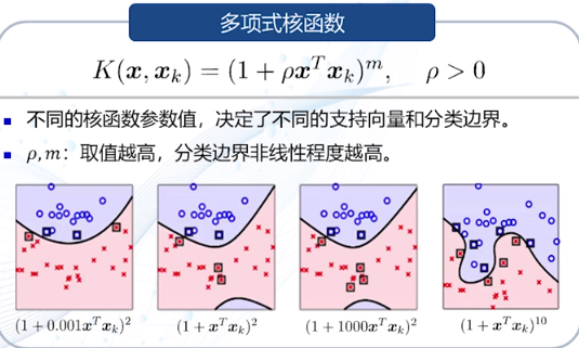
• 高斯核函数：