算法基础
算法
算法（Algorithm）：一个计算过程，解决问题的方法。
时间复杂度
时间复杂度是用来估计算法运行时间的一个式子（单位）。
当循环少一半的时候 时间复杂度O(logn)
几次关于n的循环就是n的几次方的复杂度
print('Hello World') #假如说这行代码运行时间是一个单位O(1) for i in range(n): # 这段代码的时间是O(n),因为执行了n次 print('Hello World') for i in range(n): # 这段代码是O(n*n),因为在执行了n*n次 for j in range(n): print('Hello World') for i in range(n): #这代码是O(n*n*n),执行了n的立方次 for j in range(n): for k in range(n): print('Hello World')
一般来说，时间复杂度高的算法比复杂度低的算法慢。
常见的时间复杂度（按效率排序）： O(1)<O(logn)<O(n)<O(nlogn)<O(n2)<O(n2logn)<O(n3)
空间复杂度
空间复杂度：用来评估算法内存占用大小的一个式子
空间换时间：多给它一些空间或内存，让它运行速度更快
递归
特点:
- 1.调用自身
- 2.有结束条件
def func(x): if x>0: print(x) func(x-1) print(4) # 打印结果 4 3 2 1 #因为先打印再递归
def func(x): if x > 0: func(x-1) print(x) func(4) # 打印结果 1 2 3 4 # 因为先递归，再打印
那么递归前先打印,和递归后再打印有什么不同?
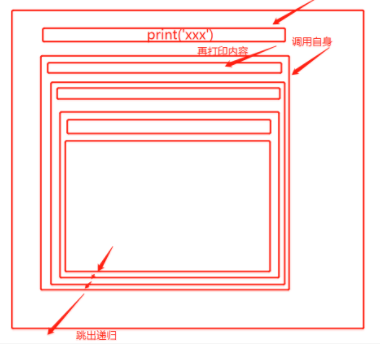
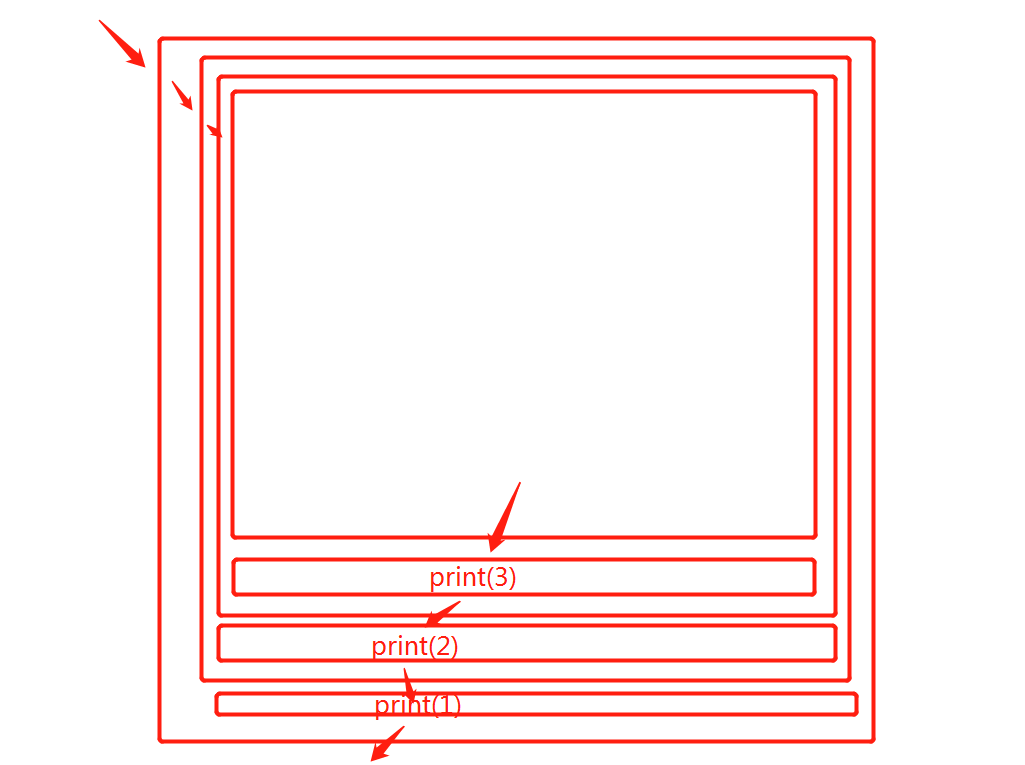
如果先递归再打印,那么打印的内容先不被执行,直到递归跳出的时候才从内到外的进行打印.
打印抱着抱着抱着我的小可爱的我的我的我
def text(n): if n>0: print('抱着',end='') text(n-1) print('的我',end='') else: print('我的小可爱',end='') text(3)
二分查找
关键点:
候选区data[0:n]
def bin_search(li, val): # li是传入的列表 val是要查找的值 low = 0 # low是起始的索引值 high = len(li) - 1 # high是末尾的索引值 while low <= high: # 满足起始索引小于末尾索引的条件就执行循环 mid = (low + high) // 2 # mid是列表的中间数的索引 if li[mid] == val: # 正好找到要查找的值的索引 return mid elif li[mid] < val: # 中间数的值小于被查找的值 low = mid + 1 # 说明val在中间数的右边 else: high = mid - 1 # 说明val在中间数的左边
尾递归二分查找:
def bin_search_rec(data_set, value, low, high): if low <= high: mid = (low + high) // 2 if data_set[mid] == value: return mid elif data_set[mid] > value: return bin_search_rec(data_set, value, low, mid - 1) else: return bin_search_rec(data_set, value, mid + 1, high) else: return
二分查找：从有序列表的候选区data[0:n]开始，通过对待查找的值与候选区中间值的比较，可以使候选区减少一半。
输出查询的列表值的下标
既然二分查找那么快为什么不全部都用二分查找呢?
因为二分查找的前提是列表是有序的,那么如何让无序的列表变成有序才是最大的问题.
列表排序
冒泡排序
冒泡排序：两层遍历，相邻的两个值，如果左边的数大于右边的数，则交换位置。
def bubble_sort(li): '''冒泡排序''' for i in range(0,len(li)-1): exchange=False for j in range(0,len(li)-i-1): # 设置终点值 if li[j]>li[j+1]: # 判断是否大于 li[j],li[j+1]=li[j+1],li[j] # 交换位置 exchange=True # 优化,如果不为true说明了没有进行交换,列表是有序的 if not exchange: return li=list(range(0,10000)) random.shuffle(li) bubble_sort(li) print(li)
时间复杂度为O(n**2)
选择排序
选择排序：遍历一趟记录最小的数，放到第一位。再遍历剩下的数，找的最小的数，继续放置。
关键点：无序区和最小数的位置。
def select_sort(li): ''' 选择排序,比较无序区最小的一个,放在有序曲后一个 :param li: 列表 :return: ''' for i in range(0,len(li)-1): min_local=i for j in range(i+1,len(li)): if li[min_local] > li[j]: min_local=j li[i],li[min_local]=li[min_local],li[i] li=list(range(0,10000)) random.shuffle(li) select_sort(li) print(li)
时间复杂度为O(n**2)
插入排序
列表被分为有序区和无序区两个部分。最初有序区只有一个元素。
每次从无序区选择一个元素，插入到有序区的位置，直到无序区变空。
代码关键点：如何找到无序区数，如何插到有序区中。
def inser_sort(li): '''插入排序, 从i开始表示摸牌的位置, 与前面的数进行相比,如果比摸的牌大则挪一位''' for i in range(1,len(li)): j=i-1 temp=li[i] while j>=0 and li[j]>temp: li[j+1] = li[j] j-=1 li[j+1]=temp li=list(range(0,10000)) random.shuffle(li) inser_sort(li) print(li)
类似于摸牌然后插入
时间复杂度为O(n**2)
快速排序
快速排序：取一个元素p（第一个元素），使元素p归位，列表被p元素分为两部分，左边都比p小，右边都比p大，然后递归完成排序。
import random def partition(li, left, right): i=random.randint(left,right) li[left],li[i] = li[i],li[left] tem=li[left] while left < right: # 列表里至少两个元素才满足这个条件 while left < right and li[right] >= tem: # 从右边边找小于tem的数 right -= 1 # 如果不小于，继续找 li[left]= li[right] # 找到比tem小的数，挪到左边 while left < right and li[left] <= tem: # 从左边找比tem大的数 left += 1 li[right]= li[left] li[left] = tem return left # 这里返回left和right是一样的 def quick_sort(li, left, right): if left < right: # 列表里至少两个元素才满足这个条件 mid = partition(li, left, right) quick_sort(li, left, mid-1) # 递归 quick_sort(li, mid+1, right) # 递归 li=list(range(10000,0,-1)) random.shuffle(li) ret=quick_sort(li,0,len(li)-1) print(li)
快速排序的时间复杂度 为O(nlogn)
堆排序
知识点介绍
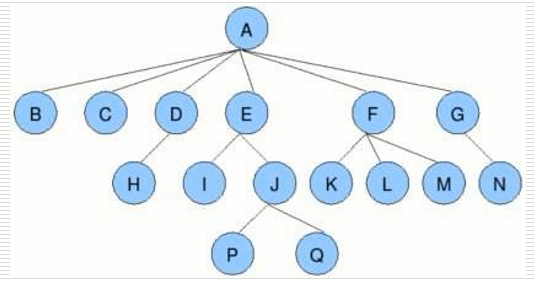
- 根节点、叶子节点
- 没有父亲的节点叫根节点,比如A, 没有孩子的节点叫叶子节点,比如BCHPQ等等
- 树的深度
- 有多少层,图示是4层
- 树的度
- 树的度势节点度的最大值比如A的度是6,E的度是2,F的度是3
- 孩子节点/父节点
- 子树
- 在同一个分支上的是子树,只有一个的也是子树
二叉树
度不超过2的树(节点最多有两个)
- 满二叉树:一个二叉树
- 如果每一层的节点都达到了最大值,则这个二叉树就是满二叉树
- 完全二叉树
- 叶节点只能出现在最下层和次下层,并且最下层的节点都集中在最左边的若干位置的二叉树
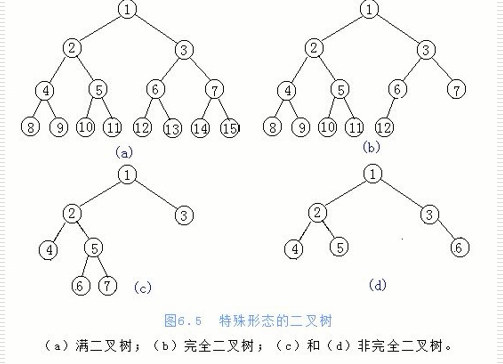
父亲节点和左孩子节点有什么位置关系?
0-1 1-3 2-5 3-7 4-9
i=2i+1
右父亲节点和孩子节点有什么位置关系?
0-2 1-4 2-6 3-8 3-10
i=2i+2
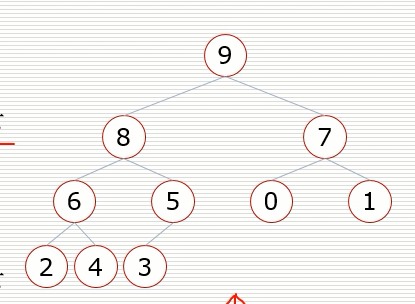
堆
- 大根堆
- 一颗完全二叉树,满足任一节点都比孩子大
- 小根堆
- 一颗完全二叉树,满足任一节点都比孩子小
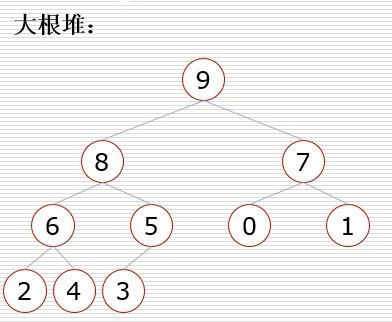
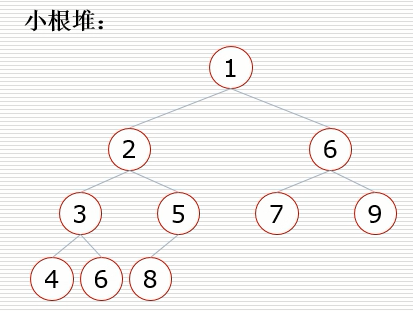
如何构建一个堆
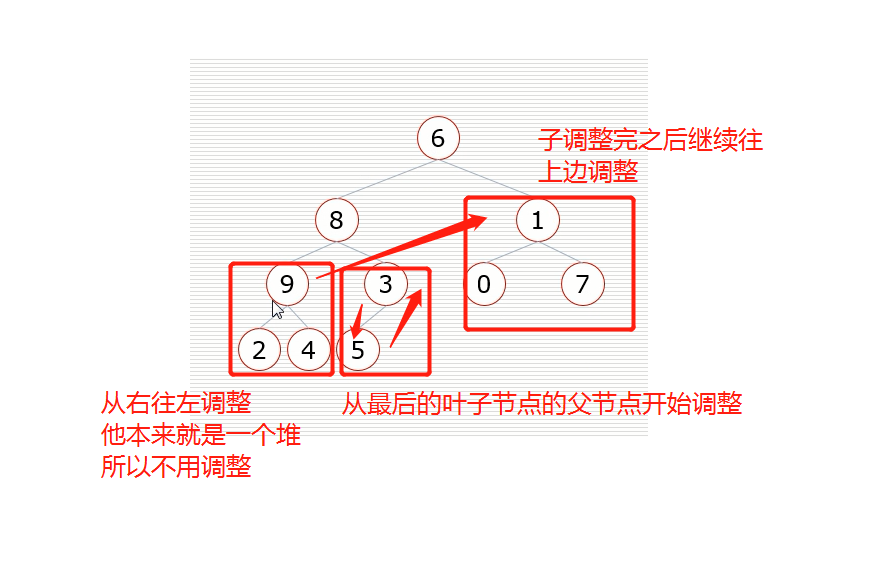
挨个出数
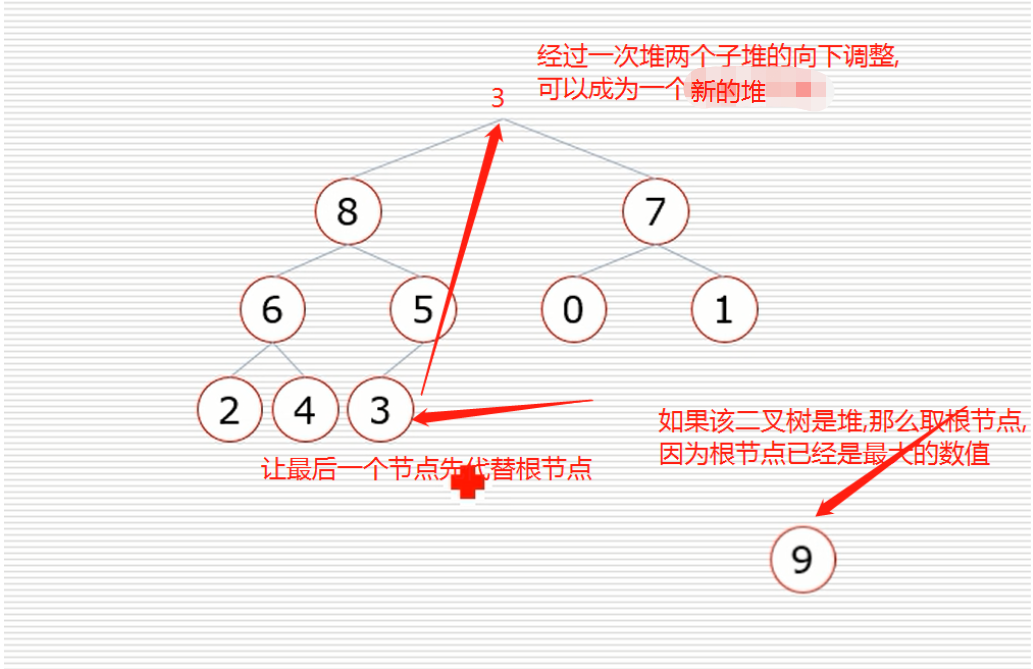
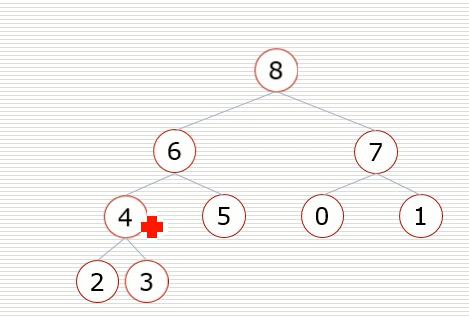
- 结果就是成立一个新的堆
再然后就是把8放到有序列表中,把最后的子节点替代根节点然后向下调整
堆排序的代码
def sift(li,low,high): temp=li[low] #根节点 i=low j=2* i + 1 # i是他的孩纸坐标 while j <= high: if j < high and li[j+1]>li[j]: #如果右孩子存在,且右孩子的值大于左孩子 j+=1 if temp<li[j]: #如果根节点的值小于他的孩子 li[i] = li[j] # 将孩子放置到根节点上 i=j #更新i的坐标值 j= 2* i +1 #更新i的坐标值 else: # 如果根节点大于两个孩子节点 li[i]=temp #放置在根节点上 结束. break else: li[i] = temp # 第二种跳出情况,temp找到自己的位置跳出,放置到i def heap_sort(li): n=len(li) # 1.建堆的过程 for i in range(n//2-1,-1,-1): # 最后一个非叶子节点的位置是n//2 -1 sift(li,i,n-1) # 2. 诶个出数 for i in range(n-1,-1,-1): li[0],li[i]=li[i],li[0] sift(li,0,i-1) import random li=list(range(0,100000)) random.shuffle(li) heap_sort(li) print(li)
归并排序
归并算法的核心就是拆分列表,在合并的过程中进行排序
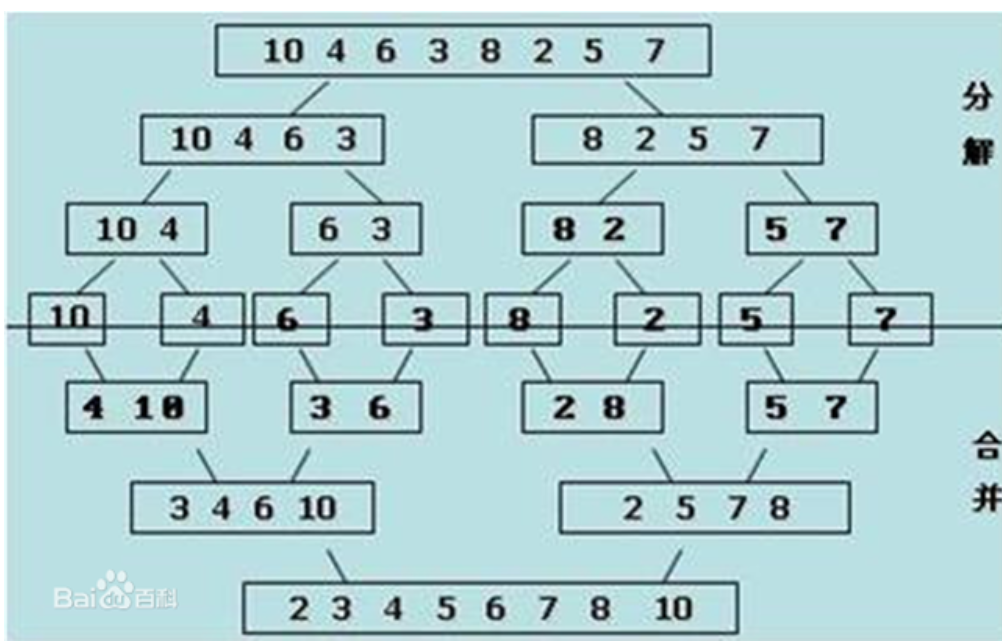
def merge(li, low, mid, high): # high是右边片段最后一个数的索引 li_tem = [] i = low # low是左边片段第一个数的索引 j = mid + 1 # mid是左边片段最大的数的索引 while i <= mid and j <= high: # 如果左右两个片段都有值，就继续取值。只要其中一个片段没值，就跳出循环。 if li[i] < li[j]: # 如果左边片段的最小值小于右边的最小值 li_tem.append(li[i]) # 就将最小的那个值取出来放到一个列表中。 i += 1 # 然后继续比较剩下的最小值 else: # 反之，就是右边的最小值小于左边的最小值 li_tem.append(li[j]) j += 1 # 然后继续比较剩下的最小值 # 跳出第一个while循环的条件是：如果左边的片段取完了，其索引i不小于mid了 # 如果右边的片段取完了，其索引j就不小于high了 # 下面的两个while循环只可能有一个执行 while i <= mid: # 这里是左偏片段还有值 li_tem.append(li[i]) i += 1 # 继续添加到列表中 while j <= high: # 这里是右边片段还有值 li_tem.append(li[j]) j += 1 # 继续添加到列表中 li[low:high+1] = li_tem def merge_sort(li, low, high): if low < high: # 保证列表至少有两个元素 mid = (low + high) // 2 # 取中间数的索引 merge_sort(li, low, mid) # 将左边的通过递归编程有序列表 merge_sort(li, mid+1, high) # 将右边的通过递归编程有序列表 merge(li, low, mid, high) # 将左右两个片段合并成一个有序列表 li = [2, 5, 7, 8, 9, 1, 3, 4, 6, 10] merge_sort(li, 0, len(li)-1) print(li)
后三种算法总结
三种排序算法的时间复杂度都是O(nlogn)
一般情况下，就运行时间而言：
- 快速排序<归并排序<堆排序
三种排序算法的缺点：
- 快速排序：极端情况下，排序效率低
- 归并排序：需要额外的内存开销
- 堆排序：在快的排序算法中相对较慢
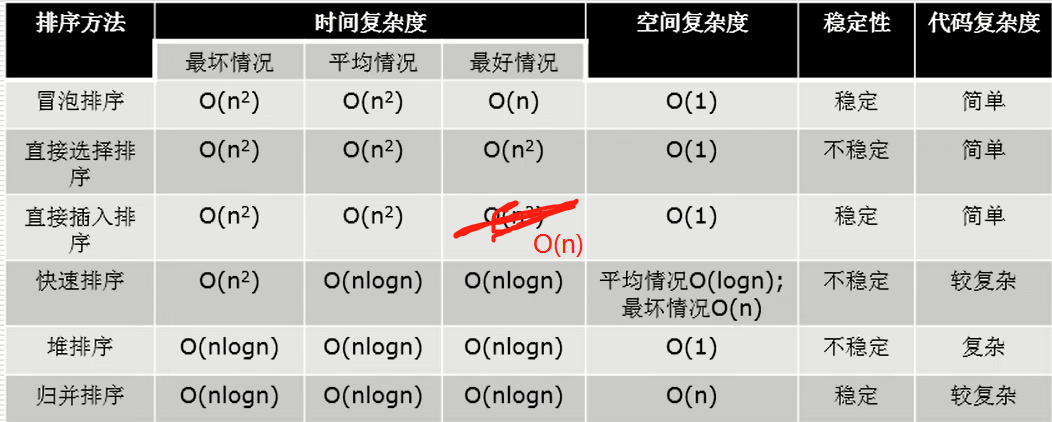
那么稳定与不稳定是什么呢?
稳定的排序是指在排序相同数字的时候不打乱原有的顺序,
比如[ (1,'alex') ,(1,'egon'),(2,'ming') ]
在排序的时候不打乱原有的数据顺序.
[ (1,'egon'),(1,'alex') ,,(2,'ming')]如果不确定是否会打乱原有顺序的则是不稳定的.
相邻比较的都是稳定的.
