平衡二叉树

平衡二叉树

平衡二叉树也是一种搜索树。

搜索树节点不同插入次序，将导致不同的深度和平均查找长度 ASL。

平衡因子（Balance Factor）:BF(T)=hL-hR，其中hL和hR分别是T的左右子树的高度。平衡二叉树（Balanced Binary Tree) 又叫 AVL树，当树不为空时，在任一节点左，右子树高度差的绝对值不超过1，即 |BF(T)|<=1。

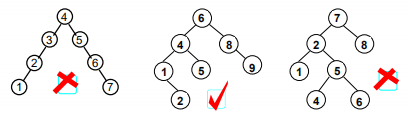
平衡二叉树的高度能够达到 \(log_2n\)

平衡二叉树的调整

任何情况都可以归结为四种模式。根据插入节点的位置不同使用不同的查找方法，同时记住平衡二叉树是搜索树，节点小于左边大于右边。平衡二叉树的四种调整方法为：右单旋，左单旋，右左双旋，左右双旋。

右单旋

按照字母大小插入三个结点，Mar, May, Nov：

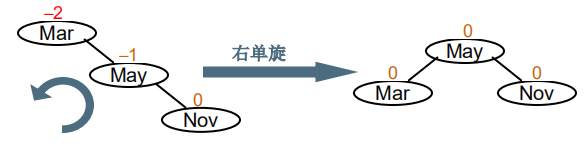
如上图左边所示，在插入 Nov 结点后，二叉树的平衡被破坏，结点Mar 的平衡因子为 -2，这个时候我们称 Mar 为不平衡的发现者，麻烦节点 Nov 在发现者右子树的右边，需要RR旋转（右单旋）。

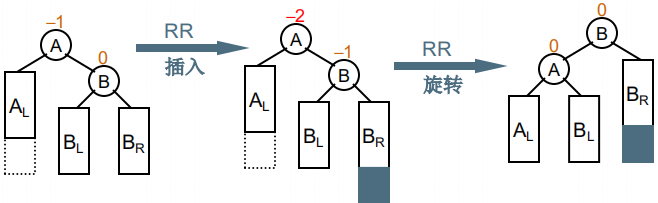
右单旋的过程如上图所示，将 B 结点调整为跟结点，\(B_L\) 调整为 A 的右结点。上图所示的是插入到右子树的右子树的右边时，当插入到右子树的右子树的位置不同时怎么处理？来看个例子：

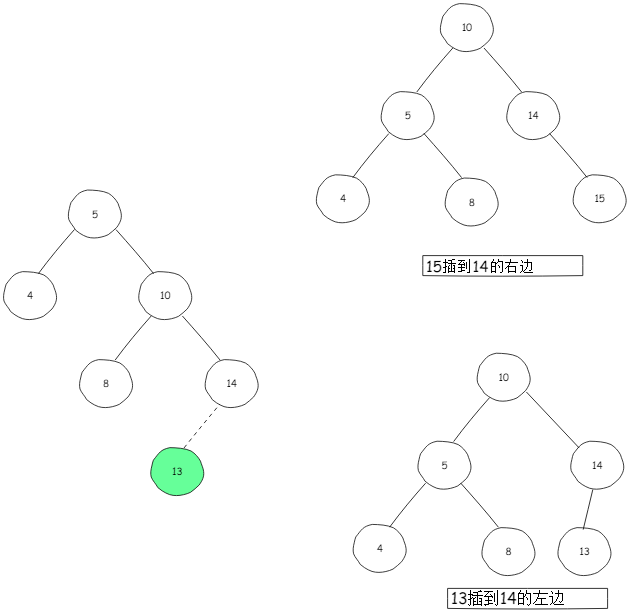
结点插到左边和右边的时候，调整平衡后位置还是不变。

// 右单旋
public AVLTree<T> singleRightRotation(AVLTree<T> a) {
    // 注意：A 必须有一个右子节点B
    // 将 A 与 B 做右单旋，更新A与B的高度，返回新的根结点B
    AVLTree<T> b = a.right;
    a.right = b.left;
    b.left = a;
    a.height = Math.max(postOrderGetHight(a.left), postOrderGetHight(a.right));
    b.height = Math.max(postOrderGetHight(b.right), a.height);

    return b;
}

左单旋

左单旋与右单旋类似，麻烦结点在发现者的左子树的左边，因而叫LL插入，需要 LL 旋转（左单旋）。

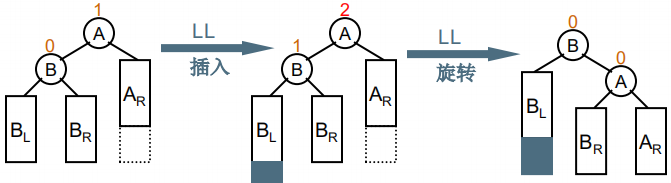
上图是左单旋的调整过程。注意，对于调整，只需要从最下层的开始调整就行。下层平衡了，上层自然也会平衡。

// 左单旋(LL旋转)
public AVLTree<T> singleLeftRotation(AVLTree<T> a) {
    // 注意：A必须有一个左子结点B
    //将 A与B做左单旋，更新A与B的高度，返回新的根结点B
    AVLTree<T> b = a.left;
    a.left = b.right;
    b.right = a;
    a.height = Math.max(postOrderGetHight(a.left), postOrderGetHight(a.right));
    b.height = Math.max(postOrderGetHight(b.left), a.height);

    return b;
}

左右双旋

对于左右双旋，麻烦结点出现在左子树的右边，因而叫 LR 插入，需要做 LR 旋转。

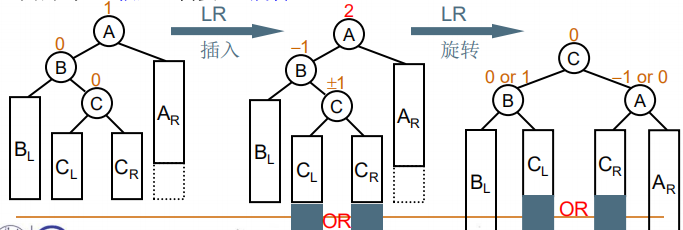
当插入的结点在 C 的左子树或者右子树下边时，就需要左右双旋，左右双旋可以看成做了两次单旋，目的是调整 A,B,C 这三个结点的位置。先将B和C 做一次右单旋，再将 C 和 A 做一次左单旋。

public AVLTree<T> doubleLeftRightRotation(AVLTree<T> a) {
    // 注意：A必须有一个左子节点B，且B必须有一个右子节点C
    // 将A、B与C做两次单旋，返回新的根结点C

    // 将B与C做右单旋，C被返回
    a.left = singleLeftRotation(a.left);
    // 将A与C做左单旋，C被返回
    return singleLeftRotation(a);
}

右左双旋

右左双旋时，麻烦结点出现在右子树的左边，因而又叫 RL 插入。

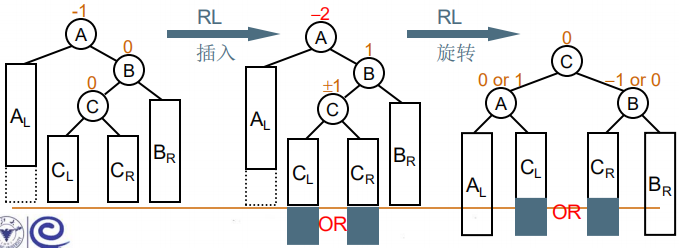
同样的，我们也可将右左双旋看成是两次单旋，将 B 和 C 做左单旋，再将 A 与 C 做右单旋。

public AVLTree<T> doubleRightLeftRotation(AVLTree<T> a) {
    // 注意：A必须有一个右子节点B，且B必须有一个左子节点C
    // 将A、B与C做两次单旋，返回新的根结点C

    // 将B与C做左单旋，C被返回
    a.right = singleRightRotation(a.right);
    // 将A与C做右单旋，C被返回
    return singleLeftRotation(a);
}

注意调整时，可能节点的位置不变，但是平衡因子需要更新。

最后，我们来看一下平衡二叉树的插入，每一次的插入都要判断平衡是否被破坏，如果发现树的平衡被破坏，根据插入的位置做上面的四种旋转重新调整成平衡二叉树。

public AVLTree<T> insert(AVLTree<T> t, T x) {
    /* 将X插入AVL树T中，并且返回调整后的AVL树 */
    if (t != null) { /* 若插入空树，则新建包含一个结点的树 */
        t = new AVLTree<>(x, null, null);
        t.height = 0;
    } /* if (插入空树) 结束 */ else if (x.compareTo(t.data) < 0) {
        /* 插入T的左子树 */
        t.left = insert(t.left, x);
        /* 如果需要左旋 */
        if (postOrderGetHight(t.left) - postOrderGetHight(t.right) == 2)
            if (x.compareTo(t.left.data) < 0)
                t = singleLeftRotation(t);      /* 左单旋 */
        else
            t = doubleLeftRightRotation(t); /* 左-右双旋 */
    } /* else if (插入左子树) 结束 */ else if (x.compareTo(t.data) > 0) {
        /* 插入T的右子树 */
        t.right = insert(t.right, x);
        /* 如果需要右旋 */
        if (postOrderGetHight(t.left) - postOrderGetHight(t.right) == -2)
            if (x.compareTo(t.right.data) > 0)
                t = singleRightRotation(t);     /* 右单旋 */
        else
            t = doubleRightLeftRotation(t); /* 右-左双旋 */
    } /* else if (插入右子树) 结束 */

    /* else X == T->Data，无须插入 */

    /* 别忘了更新树高 */
    t.height = Math.max(postOrderGetHight(t.left), postOrderGetHight(t.right)) + 1;

    return t;
}

参考

【1】浙江大学陈越老师的数据结构课程