堆

什么是堆

了解什么是堆之前，我们知道队列的概念，队列的特点是先进先出，但是有一种特殊的队列，取出元素的顺序是按照元素的优先权（关键字）大小，而不是元素进入队列的先后顺序，这就是优先队列(Priority Queue)。

若采用数组或者链表实现优先队列，总会有插入、删除或者查找中的一项操作的复杂度是\(O(N)\) 的。

若采用二叉搜索树实现，那么插入和删除都跟树的高度有关，也就是\(O(log_2N)\) 的复杂度，但是删除的时候，由于每次都要删除最大的或者最小的，这样操作几次后，会造成搜索树失去平衡，所以不能简单的使用二叉搜索树。

如果采用二叉树结构，我们更关注的应该是删除的操作，那么我们把最大的值放到根结点，左右两边也是最大值作为左右子树的根结点，每次删除只需要删除根结点。同时，为了保证树的平衡性，可以考虑使用完全二叉树来实现优先队列。

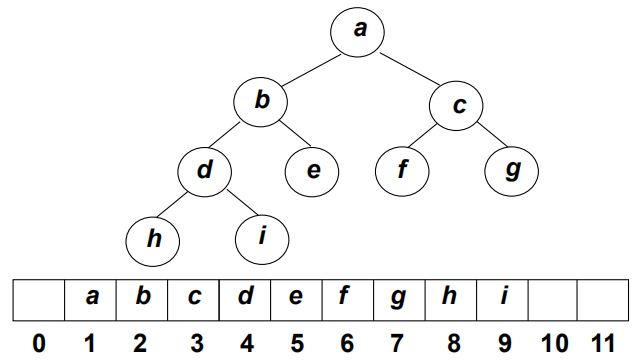
优先队列使用完全二叉树表示如上图所示，数组的第 0 个元素空着，后面的按照层序遍历的顺序存放到数组中。使用完全二叉实现的优先队列，也可以称之为堆，堆的特性如下：

• 结构性：用数组表示的完全二叉树。
• 有序性：任一结点的关键字是其子树所有结点的最大值（或最小值）
  • "最大堆"，也称 "大顶堆"：堆顶元素是整个树的最大值
  • "最小堆"，也称"小顶堆"：堆顶元素是整个树的最小值

如下图所示的几个二叉树，不是堆。

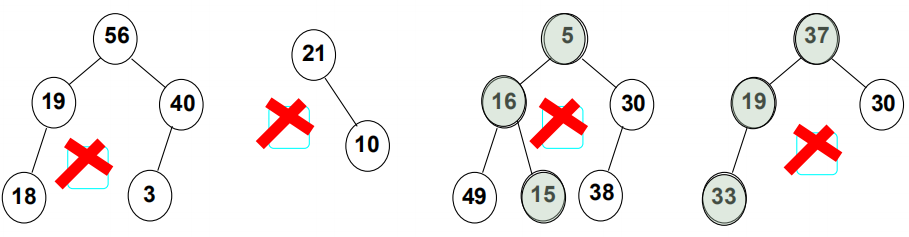
第一和第二棵二叉树虽然满足有序性，但是不是完全二叉树。第三和第四棵二叉树是完全二叉树，但是不满足有序性的特点。

注意：堆从根结点到任意结点路径上的结点顺序都是有序的！

最大堆的创建

堆的数据结构包括存储完全二叉树的数组 data，堆中当前元素个数 size，堆的最大容量 capacity。

数组的元素从1开始，0的位置定义为哨兵，方便以后更快操作。

public abstract class Heap {
    // 堆的类型定义
    protected int[] data; //存储元素的数组
    protected int size;//堆中当前元素个数
    protected int capacity; //堆的最大容量

    public Heap() {
        this.size = 0;
        this.capacity = 0;
    }

    public Heap(int[] data, int capacity) {
        this.data = data;
        this.size = 0;
        this.capacity = capacity;
        this.data[0] = Integer.MAX_VALUE;
    }

    public Heap(int maxSize) {
        this.data = new int[maxSize + 1];//最大元素从1开始
        this.size = 0;
        this.capacity = maxSize;
        this.data[0] = Integer.MAX_VALUE;// 定义哨兵，为大于最大堆中所有可能元素的值
    }

    public boolean isFull() {
        return this.size == this.capacity;
    }

    public boolean isEmpty() {
        return this.size == 0;
    }

    public abstract boolean insert(int element);
}

最大堆的插入

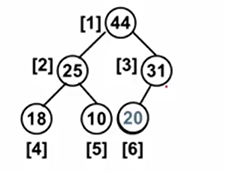
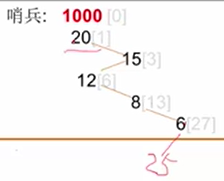
插入元素时，插入到数组的最后一个位置，这里插入的结点值为20，检查插入后仍然符合堆的两个特性，插入完成。

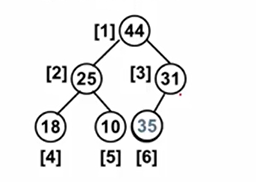
当插入的值为35的时候，当前堆的有序性被破坏了，将35和31的位置调换后就可以了。

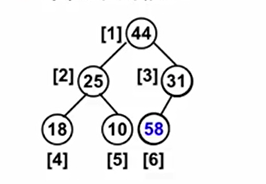
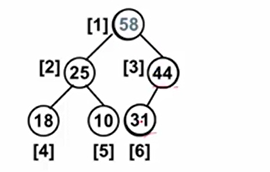
当插入的值为58的时候，58 > 31，跟31对调位置，58 > 44 继续跟根结点调换位置。调整后保证了有序性，同时，从58 -> 44 -> 31这条线也是按照从大到小的顺序。

public boolean insert(int element) {
    // 将元素X插入最大堆H，其中H->Data[0]已经定义为哨兵
    int i;

    if (isFull()) {
        System.out.println("最大堆已满");
        return false;
    }
    i = ++this.size; // i指向插入后堆中的最后一个元素的位置
    for (; this.data[i / 2] < element; i /= 2) {
        data[i] = data[i / 2]; // 向下过滤结点，对调父结点的位置
    }
    data[i] = element; // 将X插入
    return true;
}

由于我们将数组的第 0 个元素设置为哨兵，哨兵的值为一个非常大的整数值。如果没有哨兵结点，我们在循环中还需要判断 i > 1 这个条件，有了哨兵之后，循环在 i = 0 的时候就会停下来，可以少写一个条件，提高程序效率。

最大堆的删除

最大堆的删除过程就是取出根结点（最大值）元素，同时删除堆的一个结点。

删除下图的这个堆的最大值：

1. 把 31 移至根
2. 找出 31 的较大的孩子

时间复杂度为： \(T(N)=O(logN)\)

public int deleteMax() {
    // 从最大堆中取出键值为最大的元素，并删除一个结点
    int parent, child;
    int maxItem, temp;//maxItem-堆顶元素，temp-临时变量
    if (isEmpty()) {
        System.out.println("最大堆已经为空");
        return -1;
    }

    maxItem = this.data[1];//取出根结点最大值
    // 用最大堆中的最后一个元素从根结点开始向上过滤下层结点
    temp = this.data[this.size--];
    for (parent = 1; parent * 2 < this.size; parent = child) {
        child = parent * 2; // 左儿子的位置
        if (child != this.size && this.data[child] < this.data[child + 1]) {
            child++; //child 指向左右结点的较大者
        }
        if (temp > this.data[child]) {//找到位置了
            break;
        } else {//将子结点与父节点对换
            this.data[parent] = this.data[child];
        }
    }
    this.data[parent] = temp;
    return maxItem;
}

最大堆的建立

建立最大堆是将已经存在的N个元素按最大堆的要求存放在一个一维数组中。

建堆的过程可以从树的从最后一个结点的父节点开始，到根结点1，将最后一个结点的父节点所在的小堆调整为最大堆，然后向左寻找有儿子的结点，每次调整一个最大堆，直到根结点。

public void buildHeap() {
    //* 调整Data[]中的元素，使满足最大堆的有序性  *//*
    //* 这里假设所有Size个元素已经存在Data[]中 *//*

    int i;

    //* 从最后一个结点的父节点开始，到根结点1 *//*
    for (i = this.size / 2; i > 0; i--) {
        preDown(i);
    }
}

private void preDown(int p) {
    //* 下滤：将H中以Data[p]为根的子堆调整为最大堆 *//*
    int parent, child;
    int temp;

    temp = data[p]; //* 取出根结点存放的值 *//*
    for (parent = p; parent * 2 <= size; parent = child) { //这个过程与删除的过程一样
        child = parent * 2;
        if ((child != size) && (data[child] < data[child + 1]))
            child++;  //* Child指向左右子结点的较大者 *//*
        if (temp >= data[child]) break; //* 找到了合适位置 *//*
        else  //* 下滤X *//*
            data[parent] = data[child];
    }
    data[parent] = temp;
}

总结

从堆的几种操作可以发现，删除和建堆的过程，就是从上往下调整堆的有序性的过程，插入元素的过程是从下往上调整堆的有序性的过程。

参考

【1】数据结构-浙江大学