分解质因数

 

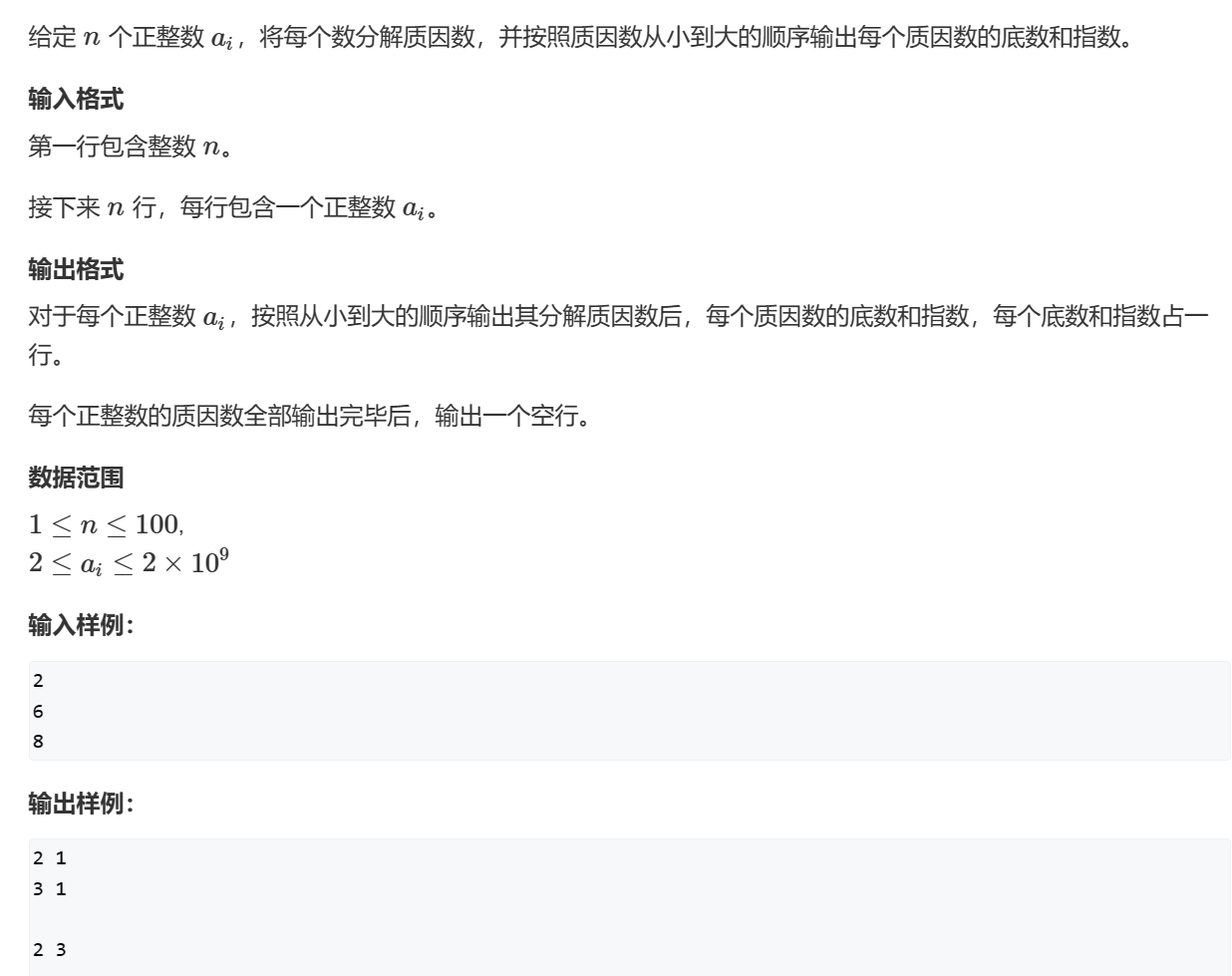
 #include<iostream>

#include<algorithm>

using namespace std;

int divide(int n){//输出底数和指数

for(int i=2;i<=n/i;i++){//可以发现，n中最多只有一个大于sqrt（n）的因子。通过反证法：如果有两个大于sqrt（n）的因子，那么相乘会大于n，矛盾。

if(n%i==0){//举个例子：16%2==0

int s;//指数

while(n%i==0){//16%2==0 ; 8%2==0 ;4%2==0; 2%2==0 ;1%2==1,不满足条件，输出

n/=i;//n=16/2=8 ; 8/2=4 ; 4/2=2;  2/2=1;

s++;//s++=1; s++=2; s++=3; s++=4;

}

cout<<i<<' '<<s<<endl;

}

//如果除到最后发现n还是大于1，则是那个唯一大于sqrt（n）的因子，即n本身

if(n>1) cout<<n<<' '<<1<<endl;

cout<<endl;//每个正整数的质因数全部输出完毕后，输出一个空行。

}

int main(){

int n;

cin>>n;

while(n--){

int x;

cin>>x;

divide(x);

}

}