树链剖分学习笔记

前言

听说树链剖分是普及组内容，但是我一直不会，最近学了一下，还做了道板子题，才感觉真正学会了树剖。

简介

树链剖分，关键就在于剖分二字。

我们可以将一棵树（如上图所示）按照子树的大小将其节点划分成两部分：重节点和轻节点（如下图所示）。

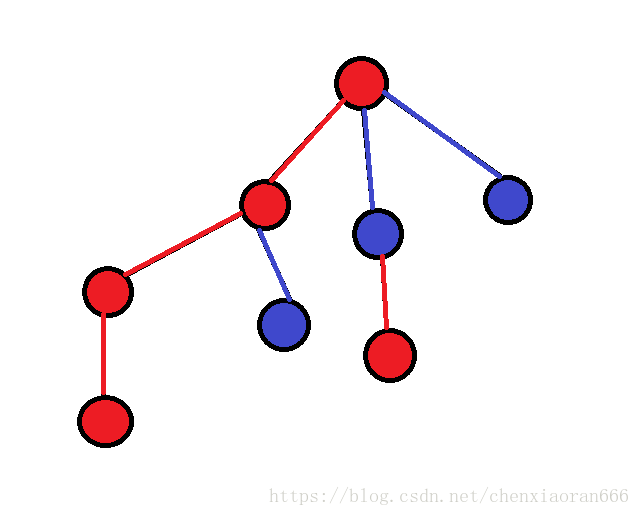
其中红色节点为重节点，蓝色节点为轻节点，红边为重链，蓝边为轻链。

概念

在刚刚的简介中，出现了一些与树链剖分相关的概念。如下：

重节点：某个节点的子节点中，size最大的节点为重节点，特殊的，根为重节点。
轻节点：与重节点恰好相反，即不是它父亲的子节点中size最大的节点为轻节点。
重边：连接重节点与重节点的边为重边。
轻边：不是连接重节点与重节点的边为轻边。即连接重节点与轻节点或轻节点与轻节点的边。
重链：由多条重边连接而成的路径。
轻链：由多条轻边连接而成的路径。

性质

1、对于一条轻边(\(fa[x]\),\(x\))，\(size(x)<=size(fa[x])/2\)。
2、从根到某一点的路径上，不超过\(O(logN)\)条轻边，不超过\(O(logN)\)条重路径。

这两个性质应该还是比较简单的，自己理解吧。

还有两个：

3、树链剖分之后，一棵子树中的所有节点是连续的。
4、树链剖分之后，一条链上的所有节点是连续的。

这两个性质应该也是挺显然的，它们为后文树链剖分的作用做了铺垫。

为什么要树链剖分？（树链剖分的作用）

树链剖分的主要作用在于，可以更好地存储并更改一棵树的信息。

在一棵普通的树上，想要修改/查询一棵子树中所有节点的信息或者两点最短路径上所有节点的信息，还是很不方便的，如果不用什么黑科技，只能\(O(n)\)修改/查询。

但是，在树链剖分之后，我们就可以快速求出要修改的区间的范围了（用到了前面提到过的性质）。然后，就可以用线段树加以维护（一般来说，树剖题都要用到线段树），时间复杂度接近于\(O(log n)\)。

树链剖分如何实现？（步骤）

• 首先，我们需要建一堆数组：

\(fa[i]\)：表示节点\(i\)的父亲。
\(son[i]\)：表示节点\(i\)的重儿子。
\(sz[i]\)：表示以节点\(i\)为根的子树的大小。
\(dep[i]\)：表示节点\(i\)的深度。
\(pos[i]\)：表示节点\(i\)树剖后的编号。
\(num[i]\)：表示树剖编号为\(i\)的节点的编号。
\(top[i]\)：表示节点\(i\)所在重链的链首。

• 定义完了一堆数组， 然后，我们要先进行一波预处理。 预处理可以分为两次\(dfs\)：
• 第一次\(dfs\)：处理出每个节点的\(fa[i]\)、\(son[i]\)、\(sz[i]\)、\(dep[i]\)。
• 第二次\(dfs\)：处理出每个节点的\(pos[i]\)、\(num[i]\)、\(top[i]\)。

代码如下：

inline void dfs1(LL x,LL de)//第一次dfs
{
    register LL i;dep[x]=de,sz[x]=1;//sz[x]初始化为1，即x节点本身
    for(i=lnk[x];i;i=e[i].nxt)//枚举每一个与x相邻的节点
    {
        if(fa[x]^e[i].to)//如果这个节点不是x的父节点，那么这个节点就是x的子节点
        {
            fa[e[i].to]=x,dfs1(e[i].to,de+1),sz[x]+=sz[e[i].to];//将这个子节点的父节点赋值为x，对该子节点继续进行预处理，并将x的size加上这个子节点的size
            if(!son[x]||sz[e[i].to]>sz[son[x]]) son[x]=e[i].to;//比较这个节点与x的重儿子的size，更新重儿子
        }
    }
}
inline void dfs2(LL x,LL col)//第二次dfs
{
    register LL i;top[x]=col,num[pos[x]=++d]=x;
    if(son[x]) dfs2(son[x],col);//优先对重儿子进行预处理，目的是使一条重链上的所有结点在树剖后编号连续
    for(i=lnk[x];i;i=e[i].nxt)//枚举每一个与x相邻的节点
        if(fa[x]^e[i].to&&son[x]^e[i].to) dfs2(e[i].to,e[i].to);//以每一个轻儿子为一条新的重链的链首继续预处理
} 

• 预处理之后，我们就可以解决修改/查询一棵子树中所有节点的信息或者两点最短路径上所有节点的信息的问题了。
• 修改
  修改时，我们可以在线段树上进行修改，这里以区间加法为例。

修改一棵子树中所有节点的信息：\(Update(1,n,1,pos[x],pos[x]+sz[x]-1,v)\)
解释：对于一棵子树，由于在树剖后节点编号是连续的，所以可以直接计算出左右区间范围，从而修改。
修改两点最短路径上所有节点的信息：\(Update\)_\((x,y,v)\)
解释：若要修改最短路上所有节点的信息，由于同一重链上节点编号是连续的，所以我们要经过一些玄学的转化，才能在线段树上进行修改，而不能直接修改。

代码如下：

inline void Update(LL l,LL r,LL rt,LL L,LL R,LL val)//在线段树上的修改（模板不解释）
{
    if(L<=l&&r<=R) {(Sum[rt]+=(r-l+1)*val%MOD)%=MOD,(Add[rt]+=val)%=MOD;return;}
    LL mid=l+r>>1;PushDown(mid-l+1,r-mid,rt);
    if(L<=mid) Update(l,mid,rt<<1,L,R,val);
    if(R>mid) Update(mid+1,r,rt<<1|1,L,R,val);
    PushUp(rt);
}

inline void Update_(LL x,LL y,LL val)//一些玄学的转化
{
    while(top[x]^top[y])//重复直至x和y在同一条链上
    {
        if(dep[top[x]]<dep[top[y]]) swap(x,y);//选择所在链较深的进行操作
        Update(1,n,1,pos[top[x]],pos[x],val),x=fa[top[x]];//将这个节点与其所在链的链首之间的区域进行修改，并将x赋值为链首的父亲
    }
    dep[x]>dep[y]?Update(1,n,1,pos[y],pos[x],val):Update(1,n,1,pos[x],pos[y],val);//此时的x和y已经在同一条链上了，所以它们之间节点编号是连续的，可以直接修改
}

• 查询
  查询的步骤与修改类似，这里以求区间和为例。

询问一棵子树中所有节点的权值和：\(Query(1,n,1,pos[x],pos[x]+sz[x]-1)\)
解释：与修改操作类似。
询问两点最短路径上所有节点的权值：\(Query\)_\((x,y)\)
解释：与修改操作类似。

代码如下：

inline LL Query(LL l,LL r,LL rt,LL L,LL R)//在线段树上查询区间和（模板不解释）
{
    if(L<=l&&r<=R) return Sum[rt];
    LL mid=l+r>>1,res=0;PushDown(mid-l+1,r-mid,rt);
    if(L<=mid) (res+=Query(l,mid,rt<<1,L,R))%=MOD;
    if(R>mid) (res+=Query(mid+1,r,rt<<1|1,L,R))%=MOD;
    return res;
}

inline LL Query_(LL x,LL y)//与修改操作类似，解释略
{
    LL res=0;
    while(top[x]^top[y])
    {
        if(dep[top[x]]<dep[top[y]]) swap(x,y);
        (res+=Query(1,n,1,pos[top[x]],pos[x]))%=MOD,x=fa[top[x]];
    }
    return (dep[x]>dep[y]?(res+Query(1,n,1,pos[y],pos[x])):(res+Query(1,n,1,pos[x],pos[y])))%MOD;
}

后记

最后，再给大家推荐洛谷上的另一道树剖板子题：【BZOJ1036】[ZJOI2008]树的统计。