网络流（一）——最大流

前言

网络流这个算法我一直都很想学，但是一直都没能学会，最近又花了一些时间去理解了一遍，才总算勉强弄懂了如何用\(Dinic\)算法去求最大流。

网络流的性质

网络流有3个很重要的性质：

• 容量限制：网络流的图上每条边都有一个容量限制\(Cap_{u,v}\)。即从点\(u\)到点\(v\)之间的流量\(Flow_{u,v}≤Cap_{u,v}\)。
• 反对称性：任意两个点\(u,v\)之间从\(u\)到\(v\)和从\(v\)到\(u\)的流量互为相反数，即\(Flow_{u,v}=-Flow_{v,u}\)。
• 流量平衡：对于任意两个不为源点且不为汇点的点\(u\)，保证它的流入量总和与流出量总和相等，即\(\sum_{x=1}^nFlow_{u,x}=\sum_{x=1}^nFlow_{x,u}\)，且源点的流出量总和与汇点的流入量总和相等，即\(\sum_{x=1}^n Flow_{s,x}=\sum_{x=1}^n Flow_{x,t}\)。

残量网络

\(Dinic\)算法中一个很重要的概念就是残量网络。

一张网络流的图上的残量网络，就是由这张图上所有\(Flow_{u,v}<Cap_{u,v}\)的边组成的图。

例如下面这张图：（\(\color{red}{红色}\)为容量，\(\color{blue}{蓝色}\)为流量）

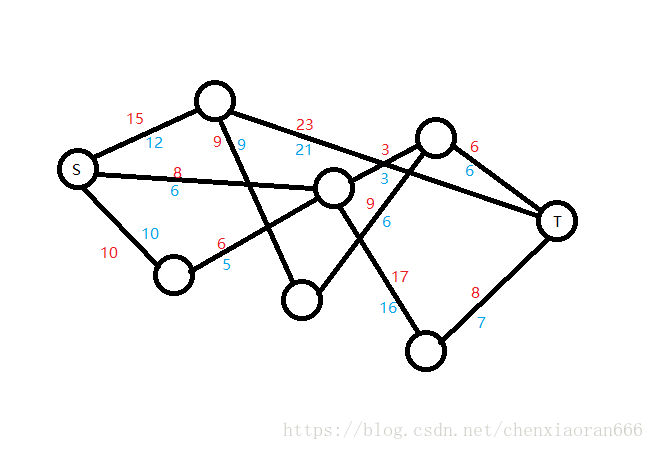
而它的残量网络就是这样的：

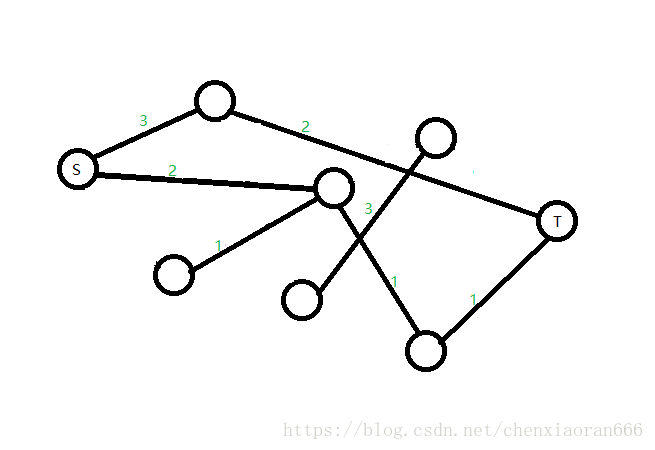
那么残量网络有什么用呢？

对于残量网络中一条从原点到汇点的路径，若这条路径上最小的权值为\(f\)，那我们就可以增加\(f\)的流量，即让从源点\(s\)出发的流量和到达汇点\(t\)的流量增加\(f\)，并将残量网络中这条路径上的权值全部减少\(f\) 。当某条边权值为0时，就将这条边从残量网络上删去。

不断重复上面过程，直至没有一条从\(s\)通向\(t\)的路径。

可以证明，此时的流量就是这张图的最大流。

具体实现

上面所说的一切的具体实现，简单而言就是一个\(BFS\)和一个\(DFS\)。

\(BFS\)

作用：\(BFS\)的作用是判断残量网络中源点与汇点是否联通，在\(BFS\)的过程中，我们还要记录每一个点被访问到的深度（这也是要用\(BFS\)而不能用\(DFS\)的原因），方便之后的\(DFS\)。

要点：在找到一条 从\(s\)到\(t\) 的路径之后，就可以立刻结束\(BFS\)了。

\(DFS\)

作用：\(DFS\)的作用是找出残量网络中一条从源点通向汇点的路，同时还要计算出能够增加的流量。

要点：①\(DFS\)的时候，每一个节点一定要转移至一个深度比它恰好多1的节点。②每一个节点在每次\(DFS\)时可以记录下当前使用到的边，每次访问到这个节点时可以直接从上次访问到的边继续往下搜索，避免重复。③当某一时刻剩余流量为0时，就离开结束搜索，可以起到一定的优化作用。

代码

struct Dinic//利用Dinic算法求最大流
{
    int ans,q[N+5],cur[N+5],Depth[N+5];//ans记录答案，q[]是BFS队列，cur[]记录每个节点当前使用到的边
    inline bool BFS()//求出是否存在一条从源点到汇点的路径
    {
        register int i,k,H=1,T=1;//初始化队列头与尾皆为1
        for(q[1]=s,i=1;i<=n;++i) Depth[i]=0;Depth[s]=1;//初始化每个节点的深度皆为1，而源点的深度为1
        while(H<=T&&!Depth[t])//只要队列未空，且还未找到一条从源点到汇点的路径
        {
            for(i=lnk[k=q[H++]];i;i=e[i].nxt)//枚举每一个节点
                if(e[i].Cap>e[i].Flow&&!Depth[e[i].to]) Depth[e[i].to]=Depth[k]+1,q[++T]=e[i].to;//如果这条路径的残量大于0，且还没被访问过，就把它加入队列
        }
        return Depth[t];//如果存在到达汇点的路径，就返回true，否则返回false
    }
    inline int DFS(int x,int f)//DFS求出在剩余流量为f时，从x到达汇点可以添加的流量之和
    {
        if(!(x^t)||!f) return f;//如果已经到达汇点，或者剩余流量为0，就返回当前流量
        register int &i=cur[x];register int t,res=0;//注意这里的i前面加了一个&，因为cur[x]记录的是x当前使用到的边，要不断更新
        for(;i;i=e[i].nxt)//枚举每一个节点
        {
            if(Depth[x]+1==Depth[e[i].to]&&e[i].Cap>e[i].Flow&&(t=DFS(e[i].to,min(f,e[i].Cap-e[i].Flow)))>0)//如果这个节点深度等于x的深度加1，且这条边残量大于0，并且可以添加的流量大于0，就更新
            {
                e[i].Flow+=t,e[((i-1)^1)+1].Flow-=t,res+=t;//将这条变得流量加上t，将这条边的反向边的流量减去t，并将res加上t
                if(!(f-=t)) return res;//如果剩余流量为0，就退出程序
            }
        }
        return res;//返回res
    }
    inline void MaxFlow()//求最大流
    {
        register int i;
        while(BFS())//只要还有从源点到汇点的路径
        {
            for(i=1;i<=n;++i) cur[i]=lnk[i];//先初始化cur[]数组为lnk[]数组
            ans+=DFS(s,1e9);//更新ans
        }
    }
}S;