【洛谷3336】[ZJOI2013] 话旧（DP）

点此看题面

大致题意： 给定一个在\([0,m]\)中连续的分段函数，其中\(f(0)=f(m)=0\)，每一个极小值都为\(0\)，且对于任意\([0,m-1]\)范围内的整数\(i\)，\(f(x)\)在\([i,i+1]\)一段上斜率为\(1\)或\(-1\)。现给定函数图像上若干个点，求符合条件的函数个数，以及函数最大值的最大值。

\(DP\)

我们设\(f_{i,0/1}\)表示考虑到第\(i\)个点，从\(a_i-1\)到\(a_i\)的直线是上升/下降的方案数。

假设当前考虑从\(A\)点到\(B\)点的一个转移，可以借助下面这张图进行理解：

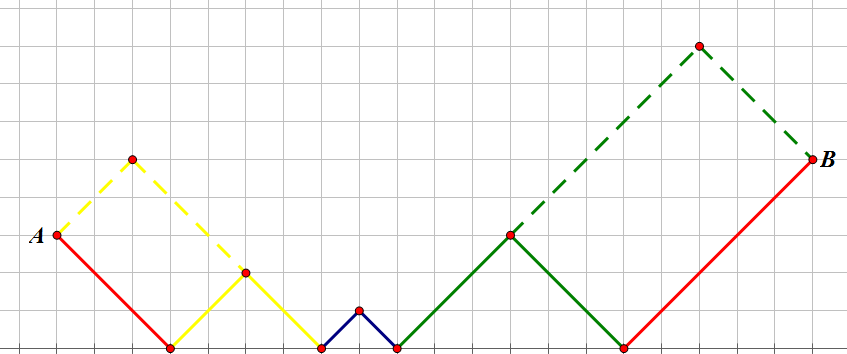
我们先找出\(A\)点向右下、\(B\)点向左下与\(x\)轴的交点，设两交点间距离为\(2k\)（可以证明一定是偶数）。

考虑两个交点之间可以一上一下一上一下地乱跳，这一方案其实就是把\(k\)个物品分成任意段的方案数，那么只要判断每个物品是否与前一个物品是否在同一段中，方案数为\(2^{k-1}\)。

首先我们发现，如果到\(B\)点的直线向上，那么就如图中实线部分所示。否则，如果到\(B\)点的直线向下，我们只要把图中绿色部分移到\(B\)的左上方（如绿色虚线部分所示）。可见，两者转移其实是一样的。

其次，如果到\(A\)的直线向下，那么就如图中实线部分所示。否则，\(A\)点可以直接向下，也可以把图中的黄色部分移到\(A\)的右上方（如黄色虚线部分所示），转移时还要额外乘上\(2\)。

用式子表示也就是：

\[f_{i,0}=f_{i,1}=2^k\times f_{i-1,0}+2^{k-1}\times f_{i-1,1} \]

但在实际转移的过程中，还需要注意两点连线恰好是一条斜率为\(1\)或\(-1\)的直线以及\(k\le0\)的特殊情况，这里就不给出转移方程了，直接见代码吧。

还有，关于第二问的最大值，显然是个非常智障的东西吧。。。（\(Upt\)：好吧，智障的是我，原来的写法被\(Hack\)了）

代码

#include<bits/stdc++.h>
#define Tp template<typename Ty>
#define Ts template<typename Ty,typename... Ar>
#define Reg register
#define RI Reg int
#define Con const
#define CI Con int&
#define I inline
#define W while
#define N 1000000
#define X 19940417
#define Gmax(x,y) (x<(y)&&(x=(y)))
using namespace std;
int n,m,a[N+5],b[N+5],f[N+5][2];map<int,int> p;map<int,int>::iterator it;
I int QP(RI y=1) {RI x=2,t=1;W(y) y&1&&(t=1LL*t*x%X),x=1LL*x*x%X,y>>=1;return t;}
class FastIO
{
	private:
		#define FS 100000
		#define tc() (A==B&&(B=(A=FI)+fread(FI,1,FS,stdin),A==B)?EOF:*A++)
		#define D isdigit(c=tc())
		char c,*A,*B,FI[FS];
	public:
		I FastIO() {A=B=FI;}
		Tp I void read(Ty& x) {x=0;W(!D);W(x=(x<<3)+(x<<1)+(c&15),D);}
}F;
int main()
{
	RI i,t,x,y;for(F.read(m),F.read(t),i=1;i<=t;++i) F.read(x),F.read(y),p[x]=y;
	for(p[0]=p[m]=0,it=p.begin();it!=p.end();++it) a[++n]=it->first,b[n]=it->second;//用map去重并排序
	RI Mx=0,k;for(f[1][1]=1,i=2;i<=n;++i) g=0,
		a[i]-a[i-1]==b[i]-b[i-1]?f[i][0]=(f[i-1][0]+(b[i-1]?0:f[i-1][1]))%X://两点连线斜率为1
		(
			a[i]-a[i-1]==b[i-1]-b[i]?f[i][1]=(f[i-1][0]+f[i-1][1])%X://两点连线斜率为-1
			(
				(k=((a[i]-b[i])-(a[i-1]+b[i-1]))/2)<0?f[i][1]=f[i-1][0],g=1://k<0，只能在上空转移
				(
					!k?f[i][0]=(f[i-1][0]+f[i-1][1])%X,f[i][1]=f[i-1][0]://k=0，向上向下都只有一种方式
						(t=QP(k-1),f[i][0]=f[i][1]=(2LL*f[i-1][0]*t+1LL*f[i-1][1]*t)%X,g=1)//一般情况
				)
			)
		),!b[i]&&(f[i][0]=0),//若纵坐标为0，不可能出现向上的情况，清零
		g?Gmax(Mx,(a[i]+b[i]-a[i-1]+b[i-1])/2):Gmax(Mx,max(b[i-1],b[i]));//统计最大值
	return printf("%d %d\n",f[n][1],Mx),0;
}