【BZOJ4910】[SDOI2017] 苹果树(恶心且卡常的树上背包)
大致题意: 给定一棵树,每个点可以被选\(a_i\)次,每次选择可以获得\(v_i\)的价值。你可以免费选择一次一条从根节点到叶节点的链上的所有节点,并再选择\(k\)次节点,要求一个节点被选择需要满足其父节点被选择过至少一次。求你能获得的最大总价值。
前言
好恶心的题目,这种东西我怎么想得出来。。。只能靠题解了。。。
而且这题卡常!(尽管我没被卡,时限\(5s\),最慢的点跑了\(3.87s\)。。。)
枚举叶节点
既然我们可以免费选择一条链,而这条链无疑让这道题变得非常恶心,于是我们可以考虑去枚举这条链,即枚举叶节点。
如图所示,假设我们选择了这条红色的链,那么一棵树就变成了红、蓝、绿\(3\)部分:
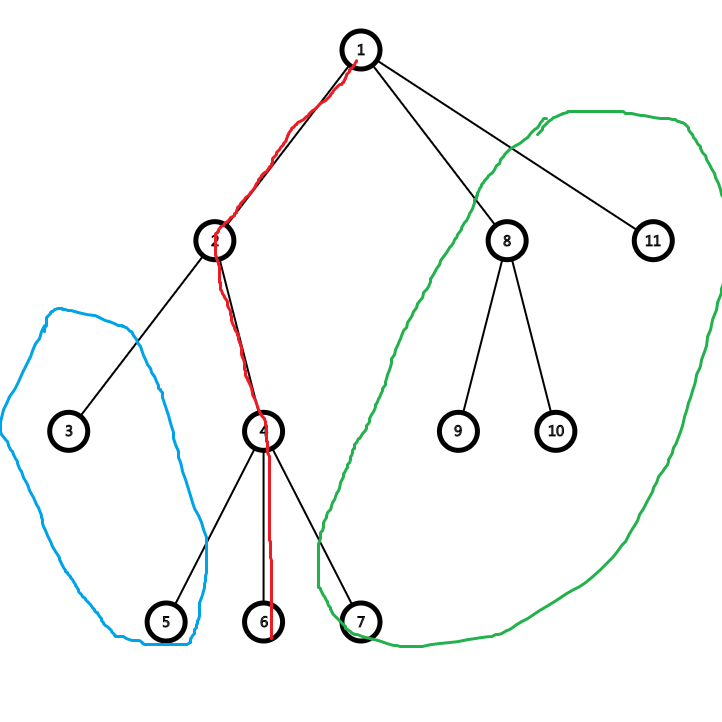
简单分析便可以发现,在蓝、绿两部分中,对于每个连通块依然需要满足题目中给定的限制,且满足这一性质就必然合法。
而对于红色这条链,由于我们已经选了一次,所以接下来其实可以随便取,这东西看似可以排序贪心。然而看看这恶心的数据范围吧,\(nk\le 2.5\times10^7\)。排序?多个\(log\)直接\(T\)飞。。。
因此这里又要使用一个玄学的方法(不过这我好像某一刻曾想到过),对于每个\(a_i>1\)的点,我们把原节点\(a_i\)修改为\(1\),同时新建一个\(a=a_i-1\)的假儿子作为该节点的子节点,可以发现它们之间依然是满足依赖关系的。
这样一来,我们就可以把假儿子归入蓝、绿两部分中一并处理。而红色部分由于\(a_i\)皆为\(1\),免费选过一次之后就不能再选,因此无法产生贡献,就不用管了。
出栈序列
接下来着重考虑如何处理蓝、绿部分。容易发现,只要反转一下边的枚举顺序,那么绿色部分就变成了蓝色部分,且容易发现蓝色部分必然可以表示为出栈序列上一段前缀。
什么是出栈序列?(就是一个打死我都想不到的东西)
我们平时记录\(dfs\)序是放在\(dfs\)函数的开头,也称作是入栈序列。
而这么一说想必你就明白了,出栈序列的\(dfs\)序就是放在\(dfs\)函数结束部分记录的。
它和一般\(dfs\)序一样,有一个很基本的性质,就是一棵子树在序列上可以表示为一段区间,并且,注意,一棵子树的根节点在区间的最右端,这一点是和一般\(dfs\)序相反的。
在这题中,出栈序列的\(dfs\)序显然发挥着不可忽视的作用。
动态规划(单调队列优化多重背包)
考虑动态规划,设\(f_{i,j}\)表示在出栈\(dfs\)序为\(1\sim i\)的节点中合法地选择\(j\)次节点的最大价值。
那么对于出栈\(dfs\)序为\(i\)的节点(设其为\(x\))显然有两种情况:选,或者不选。
- 如果选,那么我们就可以选择其子树内的节点,从\(f_{i-1,?}\)转移过来。
- 如果不选,那么我们就不能选择子树内的节点(因为要满足依赖关系),直接从\(f_{i-Sz_x,j}\)转移过来。
不选的情况显然是很简单的,而对于选的情况,我们发现,这其实就是一个多重背包。
于是就需要一个套路:单调队列优化多重背包。(我果然还是太菜,居然不知道有这种科技)
我们考虑此题中多重背包的转移方程:
我们考虑改变\(k\)的枚举内容,直接让它枚举原先的\(j-k\),即可得到:
提出和\(j\)有关的项,得到:
于是后面的\(max\)里的东西就和\(j\)无关了(当然枚举上下界还是和\(j\)有关系的)。
因此,我们可以开一个单调队列。显然一个数比另一个数出现得早,还比它小,就没用了,所以这个单调队列是单调递减的。
每次如果队首的编号小于\(j-a_i\),就把它弹掉。
于是就轻松实现了转移。
统计答案
统计答案时,考虑我们枚举了叶节点,那么可以再枚举蓝色部分选的点数\(j\)(绿色部分就选了\(k-j\))。
于是此时的答案就是蓝色部分选\(j\)个点的最大价值+根节点到该叶节点的链上的价值和+绿色部分选\(k-j\)个点的最大价值。
终于,这道题做完了。具体实现详见代码。
代码
#include<bits/stdc++.h>
#define Tp template<typename Ty>
#define Ts template<typename Ty,typename... Ar>
#define Reg register
#define RI Reg int
#define Con const
#define CI Con int&
#define I inline
#define W while
#define N 40000
#define K 500000
#define NK 50000000
#define add(x,y) (++ee,!fir[x]&&(fir[x]=ee),e[e[e[ee].nxt=lnk[x]].lst=ee].lst=0,e[lnk[x]=ee].to=y)//建边时用双向链表,因为要倒序枚边
#define Gmax(x,y) (x<(y)&&(x=(y)))
using namespace std;
int n,nn,k,ee,a[N+5],v[N+5],fir[N+5],lnk[N+5],Leaf[N+5];struct edge {int to,lst,nxt;}e[N+5];
class FastIO
{
private:
#define FS 100000
#define tc() (A==B&&(B=(A=FI)+fread(FI,1,FS,stdin),A==B)?EOF:*A++)
#define D isdigit(c=tc())
char c,*A,*B,FI[FS];
public:
I FastIO() {A=B=FI;}
Tp I void read(Ty& x) {x=0;W(!D);W(x=(x<<3)+(x<<1)+(c&15),D);}
Ts I void read(Ty& x,Ar&... y) {read(x),read(y...);}
}F;
class TreeDP
{
private:
#define f(p,i,j) f_[p][(i)*(k+1)+(j)]//注意数组使用方式
int dt,d[2][N+5],g[2][N+5],sv[N+5],Sz[N+5],f_[2][NK+N+K+5];
I void dfs0(CI x)//dfs
{
Sz[x]=1;for(RI i=lnk[x];i;i=e[i].nxt)
sv[e[i].to]=sv[x]+v[e[i].to],dfs0(e[i].to),Sz[x]+=Sz[e[i].to];
g[0][d[0][x]=++dt]=x;
}
I void dfs1(CI x)//反转枚举顺序dfs
{
for(RI i=fir[x];i;i=e[i].lst) dfs1(e[i].to);g[1][d[1][x]=++dt]=x;
}
int qi[K+5],qv[K+5];I void DP(CI p)//单调队列优化多重背包
{
for(RI i=1,j,x,t,H,T;i<=nn;++i) for(x=g[p][i],qi[H=T=1]=qv[1]=0,j=1;j<=k;++j)
{
j-qi[H]>a[x]&&++H,f(p,i,j)=max(j*v[x]+qv[H],f(p,i-Sz[x],j));//用队首计算答案
t=f(p,i-1,j)-j*v[x];W(H<=T&&t>=qv[T]) --T;qi[++T]=j,qv[T]=t;//单调队列
}
}
public:
I void Init() {memset(f_,0,sizeof(f_)),sv[1]=v[1],dt=0,dfs0(1),DP(0),dt=0,dfs1(1),DP(1);}//初始化
I void GetAns()//统计答案
{
RI i,j,t=0;for(i=1;i<=n;++i) if(Leaf[i])//枚举叶节点
for(j=0;j<=k;++j) Gmax(t,f(0,d[0][i]-1,j)+sv[i]+f(1,d[1][i]-Sz[i],k-j));//枚举左边选的点数
printf("%d\n",t);
}
}T;
int main()
{
RI Tt,i,x;F.read(Tt);W(Tt--)
{
for(F.read(n,k),nn=n,ee=0,i=1;i<=2*n;++i) fir[i]=lnk[i]=0,Leaf[i]=1;//清空
for(i=1;i<=n;++i) F.read(x,a[i],v[i]),Leaf[x]=0,
x&&add(x,i),a[i]^1&&(a[++nn]=a[i]-1,v[nn]=v[i],a[i]=1,add(i,nn));//建假儿子
T.Init(),T.GetAns();
}return 0;
}

