【BZOJ3817】Sum（类欧几里得算法）
大致题意： 求\(\sum_{i=1}^n(-1)^{\lfloor d\sqrt r\rfloor}\)。
前言
先花了\(4\)个多小时去学习类欧几里得算法，然后回来看这题。
本以为至少能推出点啥东西来的，结果依旧是一脸懵逼。
果然数学太差，看来我是真的菜。
一个巧妙的转化
观察题目中给出的式子，其中\(\lfloor d\sqrt r\rfloor\)放在指数的位置，看起来非常棘手。
因此我们考虑对\((-1)^x\)构造一个等价的函数，只要满足当\(x\)为奇数时值为\(-1\)，\(x\)为偶数时值为\(1\)即可。
于是我们就得到这样一个函数：\(1-2(x\%2)\)。（这或许可以当作一个套路？）
众所周知，\(x\%2=x-2\lfloor\frac x2\rfloor\)。再把这个东西代回原式，得到：
接下来，就是类欧几里得算法的应用了。
类欧几里得算法
刚做了板子完全不知道类欧几里得算法该如何应用的我，真的是一脸懵逼。
类欧几里得算法一般是用来求解形如\(\sum\lfloor\frac{ai+b}c\rfloor\)的式子的，而这题当中虽然没有这种式子，但却有下取整符号。
于是我们就要考虑去构造一个这种形式的式子。
为了得到上面这种形式的式子，我们设：
（则显然有\(\sum_{i=1}^n\lfloor d\sqrt r\rfloor=f(n,1,0,1),\sum_{i=1}^n\lfloor\frac{d\sqrt r}2\rfloor=f(n,1,0,2)\)）
考虑如何求出\(f(n,a,b,c)\)，此时按照类欧几里得算法的套路，我们要分类讨论。
分类讨论：\(\frac{a\sqrt r+b}c\ge 1\)
此时设\(p=\lfloor\frac{a\sqrt r+b}c\rfloor\)，则我们可以从原式中提取\(p\)，得到：
也就是说，这种情况必然能够转化为\(0<\frac{a\sqrt r+b}c<1\)的情况。
分类讨论：\(0<\frac{a\sqrt r+b}c<1\)
好玄学的做法，运用了函数思想的转化。
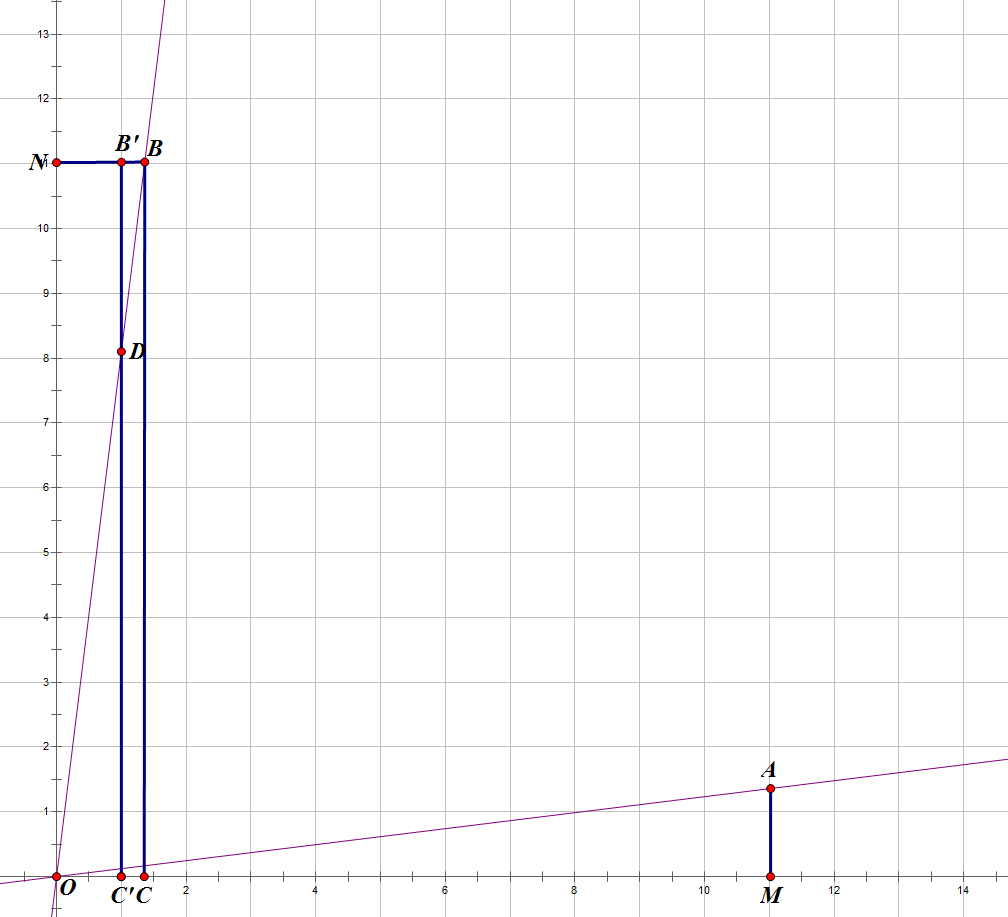
如图所示，考虑\(\sum_{i=1}^n\lfloor d\sqrt r\rfloor\)其实可以看作是一个类似于积分的形式。
但与积分不同的是，它求的是一部分区域中整点的个数。
然后我们既然把它转化成了图像，则\(f(n,a,b,c)\)的意义就变成了正比例函数\(y=\frac{a\sqrt r+b}{c}x\)（即图中的直线\(OA\)）在\(x∈[1,n]\)时整点的个数（即图中\(△AOM\)中整点的个数）。
直接求显然不好求，于是我们需要进一步转化。
考虑做出\(y\)的反函数\(y'=\frac c{a\sqrt r+b}x\)（即图中的直线\(OB\)），那么我们要求的就变成了图中\(△BON\)中整点的个数。
或许你会说，这和原来的东西并没有啥区别，一样难求。但实际上，此时我们就可以容斥了。
已知\(ON=OM=n\)，\(OC=AM=\frac{a\sqrt r+b}cn\)，显然在横坐标不为整数时不可能有整点。
也就是说我们作直线\(B'C':x=\lfloor\frac{a\sqrt r+b}cn\rfloor\)，则矩形\(BCC'B'\)中不可能有整点。
然后我们再去看这张图，就会发现，\(△BON\)中整点的个数实际上等于矩形\(ONB'C'\)中整点的个数减去\(△OC'D\)中整点的个数（注意由于这是一个斜率是无理数的正比例函数，直线上不可能存在整点，因此不会有问题）。
而\(△OC'D\)中整点的个数，实际上就是正比例函数\(y=\frac c{a\sqrt r+b}x\)在\(x∈[1,\lfloor\frac{a\sqrt r+b}cn\rfloor]\)时整点的个数。
对\(\frac c{a\sqrt r+b}\)分母有理化可得\(\frac{ac\sqrt r-bc}{a^2r-b^2}\)（这个相信大家都会），也就是说，\(△OC'D\)中整点的个数即为\(f(\lfloor\frac{a\sqrt r+b}cn\rfloor,ac,-bc,a^2r-b^2)\)。
这样一来，只要通过递归的形式，就能求出答案了。
还有一些细节问题可以看代码。
其实我写题解前还只是半懂，写完这篇题解之后就彻底理解了。。。
代码
#include<bits/stdc++.h>
#define Tp template<typename Ty>
#define Ts template<typename Ty,typename... Ar>
#define Reg register
#define RI Reg int
#define Con const
#define CI Con int&
#define I inline
#define W while
#define LL long long
using namespace std;
int n,r;
Tp I Ty gcd(Con Ty& x,Con Ty& y) {return y?gcd(y,x%y):x;}//求gcd，避免爆long long
I LL Get(CI n,LL a,LL b,LL c)//求f(n,a,b,c)
{
if(!n) return 0;LL g=gcd(gcd(a,b),c);a/=g,b/=g,c/=g;
LL p=(a*sqrt(r)+b)/c;if(p) return 1LL*n*(n+1)/2*p+Get(n,a,b-c*p,c);//如果大于1，提取整数部分转化为小于1的情况
int k=(a*sqrt(r)+b)/c*n;return 1LL*k*n-Get(k,a*c,-b*c,a*a*r-b*b);//否则容斥
}
int main()
{
RI Tt;scanf("%d",&Tt);W(Tt--)
{
scanf("%d%d",&n,&r);
if((int)sqrt(r)*(int)sqrt(r)==r) {printf("%d\n",(r&1)?(n&1?-1:0):n);continue;}//特判完全平方数，听说不然会挂
printf("%d\n",n-2*Get(n,1,0,1)+4*Get(n,1,0,2));
}return 0;
}
