【BZOJ1938】[CROATIAN2010] ALADIN(线段树+类欧几里得算法)
大致题意: 给定一个长度为\(n\)的序列,支持两种操作:给定\(L,R,A,B\),把第\(x\)个位置(\(x∈[L,R]\))上的数修改为\(((x-L+1)\times A)\%B\);给定\(L,R\),询问区间\([L,R]\)中数的和。
前言
感觉类欧几里得算法知道基本套路之后似乎并不是很难?坐等打脸。
反正这道题是我自己推出来的(尽管调试花了很久)。
线段树
这种区间修改、区间查询的问题,一看就是一个简单的线段树板子+毒瘤的数学转化。
而这道题中用到的毒瘤数学知识,就是类欧几里得算法。
考虑线段树上每个点我们需要维护一段区间的和,也就是说,我们需要快速计算\(\sum_{i=l}^r(iA\%B)\)。
一个显然的差分,若设\(G(n,A,B)=\sum_{i=1}^n(iA\%B)\),则原式等同于\(G(r,A,B)-G(l-1,A,B)\),因此只要考虑如何计算\(G\)就可以了。
而众所周知,取模有一个套路的转化:
在这个式子中,我们只需着重关注\(f(n,A,B)=\sum_{i=1}^n\lfloor\frac{iA}B\rfloor\)这一项,因为其他部分都是可以直接\(O(1)\)得到的。
而如何求解这一项,就需要类欧几里得算法了。
类欧几里得算法
对于\(f(n,A,B)\),套路地进行分类讨论:
如果\(A\ge B\),我们提取出\(\lfloor\frac AB\rfloor\)的整数部分,得到:
也就是说,这一类情况可以转化为\(A<B\)的情况做。
如果\(A<B\),我们看图:(其实这张图和【BZOJ3817】Sum是一样的)
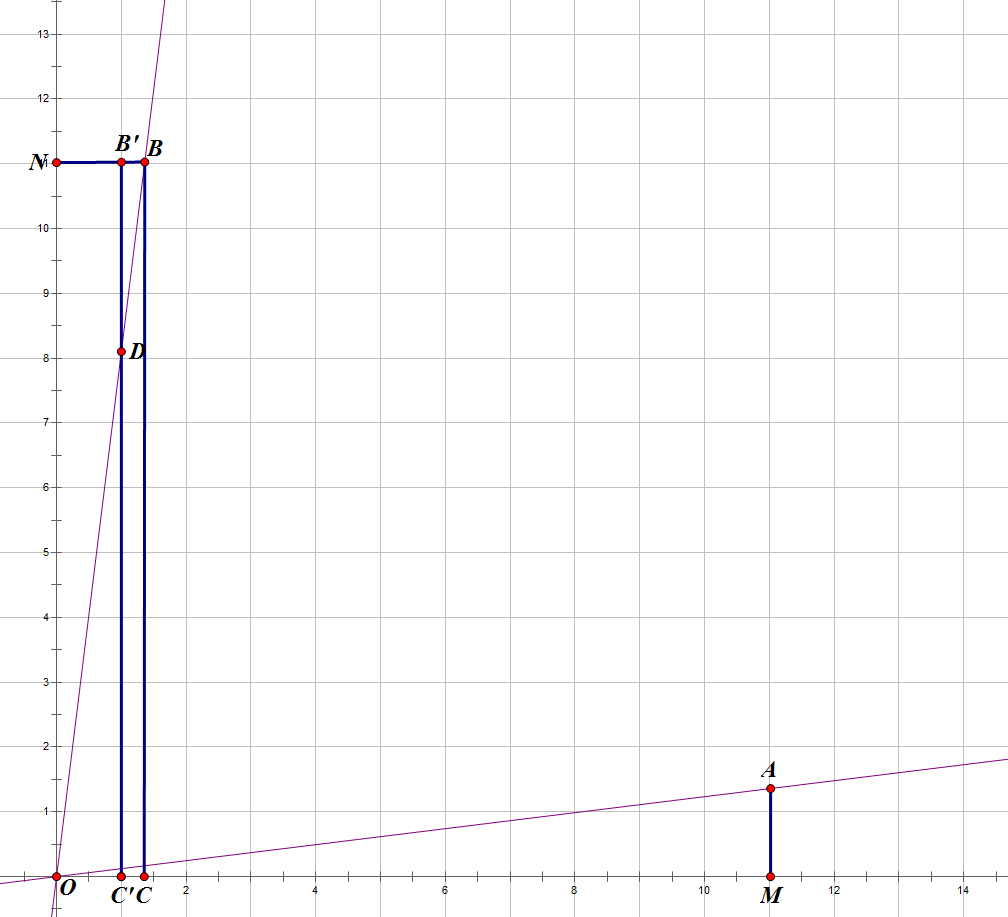
令\(y=\frac AB x\)(如直线\(OA\)所示),那么\(f(n,A,B)\)的意义就是求\(x∈[1,n]\)时在\(y\)下方的整点个数(即\(△AOM\)中整点的个数)。
然后我们作出\(y\)的反函数\(y'=\frac BA x\)(别问为什么这么做,问就是套路),那么\(△AOM\)中整点的个数就变成了\(△BON\)中整点的个数。
令\(p=\lfloor\frac AB n\rfloor\),显然\(OC'=p\)。且由于整点横坐标必然为整数,所以矩形\(BCC'B'\)中不可能有整点。
然后我们再容斥,就变成了矩形\(B'C'ON\)中整点的个数\(-△C'OD\)中整点的个数\(+\)线段\(OD\)上整点的个数。
其中,矩形\(B'C'ON\)中整点的个数就是\(n\times p\),\(△C'OD\)中整点的个数可以套用\(f\)函数变成\(f(p,B,A)\)。至于线段\(OD\)上整点的个数,我们可以在最初就把\(A,B\)同时约去它们的\(gcd\)(显然这不改变斜率,也就不改变答案),则个数显然是\(\lfloor\frac pA\rfloor\)。
可以发现\(A,B\)的变化方式和求\(gcd\)时是一样的,因此复杂度也同样是\(O(logn)\)。(这就是这个算法被称作类欧几里得算法的唯一原因)
一个有趣的小技巧
一个调试了一个多小时之后发现的小技巧。
在这道题中,很容易就会爆\(long\ long\)。
但不要慌,爆\(long\ long\)的结果在模\(2^{63}\)意义下值是相等的。我们完全可以放任它去随意爆\(long \ long\),只要在最后输出答案前给小于\(0\)的答案加上\(2^{63}\)即可.
代码
#include<bits/stdc++.h>
#define Tp template<typename Ty>
#define Ts template<typename Ty,typename... Ar>
#define Reg register
#define RI Reg int
#define Con const
#define CI Con int&
#define I inline
#define W while
#define LL long long
#define M 50000
using namespace std;
int n,dc,dv[2*M+5],op[M+5],l[M+5],r[M+5],x[M+5],y[M+5];
I int gcd(CI x,CI y) {return y?gcd(y,x%y):x;}
I LL Get(CI n,RI A,RI B)//类欧几里得算法
{
if(!n||!A) return 0;if(A>=B) return 1LL*A/B*n*(n+1)/2+Get(n,A%B,B);//若A≥B,转化为A<B
RI p=1LL*n*A/B;return 1LL*n*p-Get(p,B,A)+p/A;//容斥计算答案
}
I LL GV(CI n,CI A,CI B)//求值
{
RI g=gcd(A,B);return 1LL*A*n*(n+1)/2-1LL*B*Get(n,A/g,B/g);//计算,注意把A,B约去gcd
}
class SegmentTree
{
private:
#define PT CI l=1,CI r=dc,CI rt=1
#define LT l,mid,rt<<1
#define RT mid+1,r,rt<<1|1
#define PU(x) (O[x].V=O[x<<1].V+O[x<<1|1].V)
#define PD(x) O[x].B&&(T(x<<1,l,mid,O[x].A,O[x].B,O[x].K),\
T(x<<1|1,mid+1,r,O[x].A,O[x].B,O[x].K),O[x].A=O[x].B=O[x].K=0)
#define T(x,l,r,a,b,k) (O[x].A=a,O[x].B=b,\
O[x].K=k,O[x].V=GV(dv[r]-(k),a,b)-GV(dv[(l)-1]-(k),a,b))
struct node {int A,B,K,S[2];LL V;}O[M<<4];
public:
I void U(CI L,CI R,CI A,CI B,PT)//区间赋值
{
if(L<=dv[l-1]+1&&dv[r]<=R) return (void)T(rt,l,r,A,B,L-1);int mid=l+r>>1;PD(rt),
L<=dv[mid]&&(U(L,R,A,B,LT),0),R>dv[mid]&&(U(L,R,A,B,RT),0),PU(rt);
}
I LL Q(CI L,CI R,PT)//询问
{
if(L<=dv[l-1]+1&&dv[r]<=R) return O[rt].V;int mid=l+r>>1;PD(rt);
return (L<=dv[mid]?Q(L,R,LT):0)+(R>dv[mid]?Q(L,R,RT):0);
}
}S;
int main()
{
RI Qt,i;for(scanf("%d%d",&n,&Qt),i=1;i<=Qt;++i) scanf("%d%d%d",op+i,l+i,r+i),
op[i]^2&&(scanf("%d%d",x+i,y+i),x[i]%=y[i]),dv[++dc]=l[i]-1,dv[++dc]=r[i];//存下操作以离散化
sort(dv+1,dv+dc+1),dc=unique(dv+1,dv+dc+1)-dv-1;LL t;
for(i=1;i<=Qt;++i) op[i]^2?S.U(l[i],r[i],x[i],y[i]),0//修改
:(t=S.Q(l[i],r[i]),printf("%lld\n",t<0?t+(1ull<<63):t));return 0;//询问,对于小于0的答案加上2^63
}

