【AtCoder】AtCoder Grand Contest 039 解题报告
A:Connection and Disconnection(点此看题面)
大致题意: 给你一个字符串,将它重复\(k\)次。进行尽量少的操作,每次修改一个位置上的字符,使得不存在两个相邻位置上字符相同。求最少操作次数。
一个很\(naive\)的想法,就是将原串直接扫一遍,遇到与前一位相同的字符,就修改这一位字符为一个不存在的字符,并将计数器加\(1\)。最后将计数器乘上\(k\)。
然后,比较此时串首与串尾是否相同(注意是此时,因为上面操作中可能会修改串尾),如果相同,那么对于这\(k\)次重复的\(k-1\)个首尾交点,我们都需要修改,因此将计数器再加上\(k-1\)。
如果仅仅这样交上去,会\(WA\)掉两个点。
但只要再仔细推一推,就可以找到刚才想法的漏洞。
首先,我们需要特判所有字符相同的情况,此时答案就是\(\lfloor\frac{|S|\times k}2\rfloor\),然后你就发现你能多过一个点。
其次,我们需要将原串倒着再执行一遍上述操作,然后将正着和倒着两种情况下的答案取\(min\)。其实也就相当于一种是尽量取串尾,一种是尽量取串头,这可能会影响到首尾交点处是否需要修改。
这样一来,就能过了此题。
#include<bits/stdc++.h>
#define Tp template<typename Ty>
#define Ts template<typename Ty,typename... Ar>
#define Reg register
#define RI Reg int
#define Con const
#define CI Con int&
#define I inline
#define W while
#define N 100
using namespace std;
string s,p;int n,k;
I bool Check() {for(RI i=1;i^n;++i) if(s[i]^s[i-1]) return false;return true;}//检查是否所有字符相同
int main()
{
RI i;long long t1=0,t2=0;if(cin>>s>>k,n=s.length(),Check()) return printf("%lld",(1LL*n*k)>>1),0;//特判所有字符相同
for(p=s,i=1;i^n;++i) s[i]==s[i-1]&&(s[i]=0,++t1);t1*=k,s[0]==s[n-1]&&(t1+=k-1);//正着求答案
for(s=p,i=n-2;~i;--i) s[i]==s[i+1]&&(s[i]=0,++t2);t2*=k,s[0]==s[n-1]&&(t2+=k-1);//倒着求答案
return printf("%lld",min(t1,t2)),0;//输出答案
}
B:Graph Partition(点此看题面)
大致题意: 一张无向连通图,让你把点集分到若干个集合中,使得对于图上任意一条边,满足其连接的两个节点在相邻的两个集合中。求最多能分成多少个集合。
数据范围很小......
因此,我们可以直接枚举一个起点,然后\(BFS\)求出答案。
这一过程应该还是比较简单的,直接上代码了吧。
#include<bits/stdc++.h>
#define Tp template<typename Ty>
#define Ts template<typename Ty,typename... Ar>
#define Reg register
#define RI Reg int
#define Con const
#define CI Con int&
#define I inline
#define W while
#define N 200
using namespace std;
int n,p[N+5],q[N+5],a[N+5][N+5];
I int BFS(CI x)//BFS求答案
{
for(RI i=1;i<=n;++i) p[i]=0;//清空
RI i,k,H=1,T=1;p[q[1]=x]=1;W(H<=T) for(k=q[H++],i=1;i<=n;++i)
if(a[k][i]) {if(p[i]&&p[i]^(p[k]-1)&&p[i]^(p[k]+1)) return -1;!p[i]&&(p[q[++T]=i]=p[k]+1);}//若矛盾返回-1,否则赋值并加入队列
return p[q[T]];//返回答案
}
int main()
{
RI i,j,t,ans=-1;string s;for(scanf("%d",&n),i=1;i<=n;++i)
for(cin>>s,j=1;j<=n;++j) s[j-1]&1&&(a[i][j]=1);
for(i=1;i<=n;++i) ans<(t=BFS(i))&&(ans=t);return printf("%d",ans),0;//枚举起点输出答案
}
C:Division by Two with Something(点此看题面)
大致题意: 给你一个\(n\)位二进制数\(x\),求出对于\(0\sim x\)的每一个\(k\),进行奇数去末位\(1\)在首位加\(0\)、偶数去末位\(0\)在首位加\(1\)的操作后,第一次变回\(k\)本身的操作次数之和。
首先,不难发现,无论什么数,在\(2n\)次操作后,都必然会变回自身。
否则,考虑一个二进制数\(t\),它第一次变回自身的操作次数。
我们将\(t\)复制一遍并取反,然后放在它的前面,那么,进行\(p\)次\((p\le n)\)操作后,其实就是这个串中的\([n-p+1,2n-p]\)一段。
由于一个数不可能通过奇数次变回自身,所以我们假设进行\(2i\)次操作能使\(t\)变回自身,又因进行\(2n\)次操作后\(t\)必然能变回自身,所以我们可以确定,\(i|n\)。
则,我们可以把\(t\)划分成长度为\(i\)的\(\frac ni\)段,就能发现其中奇数段之间相等,偶数段之间相等,奇数段与偶数段是互相取反的结果。注意,如果\(\frac ni\)为偶数,就说明\(t=\sim t\),这显然是不可能的,因此\(\frac ni\)必然为奇数。
也就是说,我们只要枚举\(n\)的一个因数\(i\),满足\(\frac ni\)为奇数,那么以任意一段合法的长度为\(i\)的二进制数作为开头,都必然存在唯一一个数使其满足经过\(2i\)次操作能变回自身。而此处的合法,只要满足字典序小于等于题目中给出的\(x\)即可。
但要注意,这里求出的经过\(2i\)次操作能变回自身的数不一定是经过\(2i\)次操作后第一次变回自身,因此还需要通过容斥来求出真正的答案。
#include<bits/stdc++.h>
#define Tp template<typename Ty>
#define Ts template<typename Ty,typename... Ar>
#define Reg register
#define RI Reg int
#define Con const
#define CI Con int&
#define I inline
#define W while
#define N 200000
#define X 998244353
#define Inc(x,y) ((x+=(y))>=X&&(x-=X))
using namespace std;
int n;int a[N+5],b[N+5],f[N+5],g[N+5];
int main()
{
RI i,j,p,k=0,t=0,cnt=0;string s;
for(scanf("%d",&n),cin>>s,i=1;i<=n;++i) a[i]=s[i-1]&1;//读入
for(i=1;i<=n;++i) if(!(n%i)&&(n/i)&1)//枚举一个符合条件的i
{
for(f[++k]=i,j=1;j<=i;++j) g[k]=(g[k]<<1|a[j])%X;++g[k];//计算合法数的个数上界,只需判断是否能够达到上界
for(j=1;j<=i;++j) b[j]=a[j];
for(j=i+1;j<=n;++j) if(b[j]=b[j-i]^1,a[j]^b[j]) {a[j]<b[j]&&--g[k];break;}//若超出范围,则个数无法达到上界,减1
}
for(i=1;i<=k;++i) for(j=i+1;j<=k;++j) !(f[j]%f[i])&&Inc(g[j],X-g[i]);//容斥
for(i=1;i<=k;++i) t=(2LL*f[i]*g[i]+t)%X,Inc(cnt,g[i]);//统计答案
return printf("%d",t),0;//输出答案
}
D:Incenters(点此看题面)
大致题意: 给你圆上\(n\)个点(以角度的形式给出),求任选其中三个点后这三点构成三角形的内心坐标的平均值。
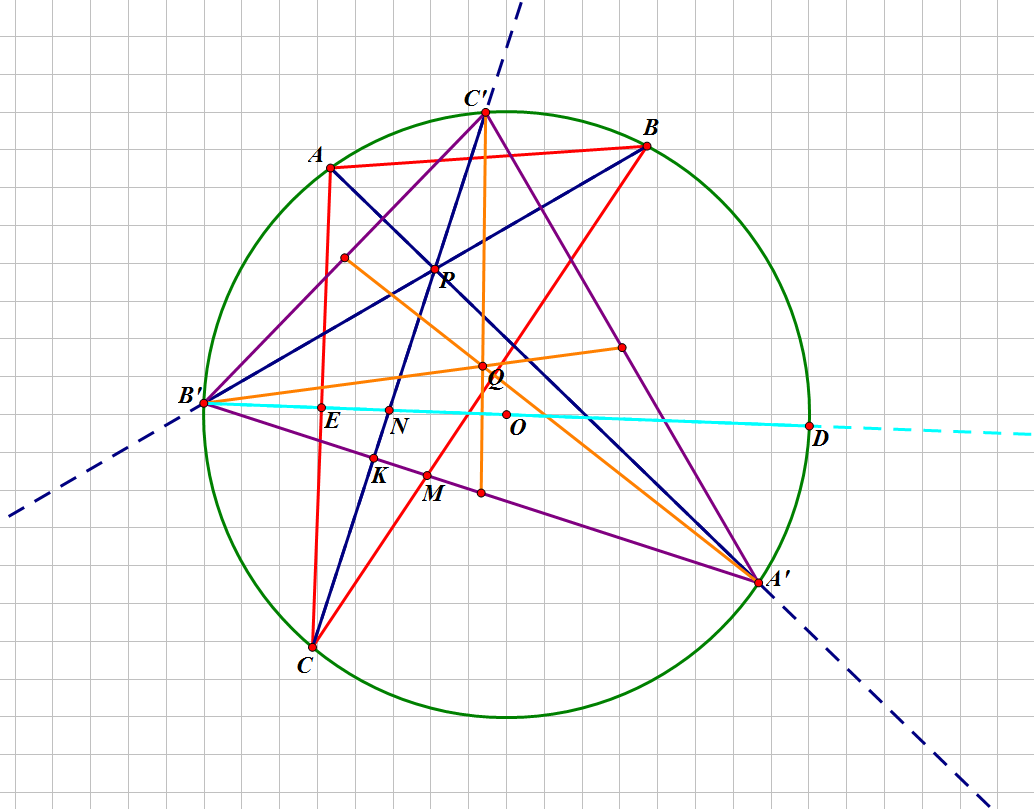
几何画板是个好东西......
按照题意,假设\(A,B,C\)三点是我们选出的点,连结\(AB,AC,BC\),就得到如图所示的红色三角形。
然后,作出\(\triangle ABC\)三个顶点的角平分线并延长分别交\(⊙ABC\)于点\(A',B',C'\),三条角平分线交于点\(P\),点\(P\)即为所求的内心。
连结\(A'B',A'C',B'C'\),就得到如图所示的紫色三角形。
通过几何画板,我们可以发现两个至关重要的结论:
结论一: 点\(C'\)是弧\(AB\)的中点。
\(\because CC'\)平分\(\ang ACB,\therefore\ang ACC'=\ang BCC',\therefore\)弧\(AC'=\)弧\(BC',\therefore C'\)是弧\(AB\)的中点\(.\)
结论二: 点\(P\)是\(\triangle A'B'C'\)的垂心。
连结\(B'O\)并延长,分别交\(AC,CC',⊙O\)于点\(E,N,D.\)
\(\because B'\)是弧\(AC\)的中点\(,\therefore B'D⊥AC,\therefore \ang CEN=90\)度\(.\)
\(\because A'\)是弧\(BC\)的中点\(,B'\)是弧\(AC\)的中点\(,C'\)是弧\(AB\)的中点\(,\therefore\)弧\(AC'=\frac12\)弧\(AB,\)弧\(B'C=\frac12\)弧\(AC,\)弧\(A'C=\frac 12\)弧\(BC,\therefore\)弧\(AC'+\)弧\(B'C+\)弧\(A'C\)的度数为\(180\)度\(.\)
\(\because B'D\)是直径\(,\therefore\)弧\(B'C+\)弧\(A'C+\)弧\(A'D\)的度数为\(180\)度\(,\therefore\)弧\(AC'=\)弧\(A'D,\therefore\ang ACC'=\ang A'B'D.\)
\(\because CC'\)平分\(\ang ACB,\therefore \ang BCC'=\ang ACC',\therefore\ang BCC'=\ang A'B'D.\)
又\(\because\ang CKM=\ang B'KN,\therefore\ang CMK=\ang B'NK.\)
\(\therefore \ang CKM=\ang CEN=90\)度\(,\therefore CC'⊥A'B'.\)
同理,最终可得,\(P\)是\(\triangle A'B'C'\)的垂心。
由结论二,我们作出\(\triangle A'B'C'\)的三条中线(图中三条黄色线段),其交点\(Q\)即为\(\triangle A'B'C'\)的重心。
又因为\(⊙O\)是\(\triangle A'B'C'\)的外接圆,所以点\(O\)是\(\triangle A'B'C'\)的外心。
有了外心、重心、垂心,根据欧拉线定理,\(O,P,Q\)三点共线,\(PQ=2OQ\)。所以\(OP=3OQ\),即点\(P\)的横纵坐标都是点\(Q\)的三倍。
而重心\(Q\)的坐标,实际上就是\(\triangle A'B'C'\)三点坐标的平均值。
综合结论一,我们可以\(O(n^2)\)枚举圆上两点\(A,B\)。
那么当点\(C\)在\(AB\)优弧上时,\(C'\)就是\(AB\)劣弧的中点,当点\(C\)在\(AB\)劣弧上时,\(C'\)就是\(AB\)优弧的中点。
设\(AB\)优弧上有\(x\)个点,劣弧上有\(y\)个点,那么\(C'\)的坐标期望就是\(AB\)劣弧中点坐标乘\(\frac x{x+y}\)加\(AB\)优弧中点坐标乘\(\frac y{x+y}\),其中显然\(x+y=n-2\)。
由于题中给出的是点的角度,因此弧中点坐标就是角度的平均值,这一点还是很良心的。
这样一来,我们就求出当选择\(AB\)作为红色三角形一边时,紫色三角形一点的坐标期望。
而\(AB\)作为红色三角形一边的概率是\(\frac 1{C_n^2}=\frac 2{n(n-1)}\),因此将所有的\(A,B\)求出的坐标期望求和并乘上\(\frac 2{n(n-1)}\),就是最后紫色三角形重心的坐标期望。
然后乘\(3\),即为答案。
#include<bits/stdc++.h>
#define Tp template<typename Ty>
#define Ts template<typename Ty,typename... Ar>
#define Reg register
#define RI Reg int
#define Con const
#define CI Con int&
#define I inline
#define W while
#define N 3000
#define DB double
using namespace std;
int n,l,a[N+5];const DB pi=acos(-1);
struct Point
{
DB x,y;I Point() {x=y=0;}I Point(Con DB& a):x(cos(2*pi*a/l)),y(sin(2*pi*a/l)){}//根据角度算坐标
I Point(Con DB& a,Con DB& b):x(a),y(b){}
I Point operator + (Con Point& t) Con {return Point(x+t.x,y+t.y);}
I Point operator * (Con DB& t) Con {return Point(x*t,y*t);}
}ans;
int main()
{
RI i,j;for(scanf("%d%d",&n,&l),i=1;i<=n;++i) scanf("%d",a+i);//读入角度
for(sort(a+1,a+n+1),i=1;i<=n;++i) for(j=i+1;j<=n;++j)//枚举两个点
ans=ans+Point((a[i]+a[j])/2.0)*(1.0*(n-2-(j-i-1)*2)/(n-2));//统计
return ans=ans*(6.0/n/(n-1)),printf("%.10lf %.10lf",ans.x,ans.y),0;//计算并输出答案
}
E:Pairing Points(点此看题面)
大致题意: 一个圆上有\(2n\)个点,有若干对点之间可以连边。求有多少种连边方案,使得每个点恰好连出一条边,并满足边之间连通且无环。
我们定义一个基本局面\((l,r,mid)(l<mid<r)\)表示满足以下条件的一个局面:
- \([l,mid-1],[mid+1,r]\)中的点都还未连边,且只会跟\([l,mid-1],[mid+1,r]\)中的点连边。
- \(mid\)已和\([l,r]\)外的一点连边。
考虑一开始,先对于\(1\)号点,为其枚举一个\(x\)号点,表示\(1\)与\(x\)相连,那么我们就得到一个局面\((2,2n,x)\)。
可以发现,对于某一局面,若\([l,mid-1]\)中的一点要和\([mid+1,r]\)中的一点相连,就必然与以\(mid\)为一端的线段有交。而如果与\(mid\)的线段有交的某两条线段再相交,就会有环。因此,这样的一组线段它们的端点应该是单调的。
所以,我们可以枚举最靠外的一条与\(mid\)的线段有交的线段\(i,j\),其中\(i∈[l,mid-1],j∈[mid+1,r]\)。
考虑对于\([i+1,mid-1]\)中的一点,它如果要向\([i+1,mid-1]\)这一范围之外的点连边,必然会经过\(i\)的线段或\(mid\)的线段中的一条。由于不能存在环,则必然是以一个点\(p\)为界,其中\([i+1,p]\)中的点向外连边时与\(i\)的线段有交,\([p+1,mid-1]\)中的点向外连边时与\(mid\)的线段有交。
同理,在\([mid+1,j-1]\)中,我们也能找到符合类似定义的一点\(q\)。
然后我们就发现,对于\((l,p,i),(p+1,q-1,mid),(q,r,j)\)这三个局面,它们都符合上面对于基本局面的定义。
因此,我们只要继续递归处理对应局面即可。
#include<bits/stdc++.h>
#define Tp template<typename Ty>
#define Ts template<typename Ty,typename... Ar>
#define Reg register
#define RI Reg int
#define Con const
#define CI Con int&
#define I inline
#define W while
#define N 20
#define LL long long
using namespace std;
int n,a[2*N+5][2*N+5];LL f[2*N+5][2*N+5][2*N+5];
I LL DP(CI l,CI r,CI mid)//处理某一局面
{
if(~f[l][r][mid]) return f[l][r][mid];if(l==r) return 1;if(l==mid||r==mid) return 0;//判边界
RI i,j,p,q;LL t=0;for(i=l;i^mid;++i) for(j=r;j^mid;--j) if(a[i][j])//枚举最靠外的边
for(p=i;p^mid;++p) for(q=j;q^mid;--q) t+=DP(l,p,i)*DP(p+1,q-1,mid)*DP(q,r,j);//枚举两个分界点,递归求答案
return f[l][r][mid]=t;//记忆化,返回答案
}
int main()
{
RI i,j;string s;memset(f,-1,sizeof(f));
for(scanf("%d",&n),i=1;i<=2*n;++i) for(cin>>s,j=1;j<=2*n;++j) a[i][j]=s[j-1]&1;//读入
LL t=0;for(i=2;i<=2*n;++i) a[1][i]&&(t+=DP(2,2*n,i));return printf("%lld",t),0;//枚举与1相对的点,统计答案并输出
}
F:Min Product Sum(占坑待填)
\(F\)题显然不可做,看题解看了半个小时也没看懂。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号