【AtCoder】AtCoder Grand Contest 030 解题报告
\(A\):Poisonous Cookies(点此看题面)
大致题意: 有\(A\)块难吃的含解药的饼干、\(B\)块好吃的含解药的饼干,\(C\)块好吃的含毒药的饼干。不能连吃两块含毒药的饼干,问最多能吃几块好吃的饼干。
考虑\(B\)块好吃的含解药的饼干一定能吃完,好吃的含毒药的饼干不能吃超过\(A+B+1\)块(否则就会被毒死),因此答案为\(B+\min\{C,A+B+1\}\)。
#include<bits/stdc++.h>
#define Tp template<typename Ty>
#define Ts template<typename Ty,typename... Ar>
#define Reg register
#define RI Reg int
#define Con const
#define CI Con int&
#define I inline
#define W while
using namespace std;
int A,B,C;
int main()
{
return scanf("%d%d%d",&A,&B,&C),printf("%d\n",B+min(C,A+B+1)),0;//读入+输出
}
\(B\):Tree Burning(点此看题面)
大致题意: 一个周长为\(m\)的圆上有\(n\)棵树,其中第\(i\)棵树逆时针方向到原点距离为\(x_i\)。从原点出发,只要还存在树,你就可以选择一个方向走到最近的一棵树并把这棵树烧掉。求能走的最大距离。
一个显然的贪心,肯定是先沿某个方向一直走到某一棵树,然后不断变向走。
枚举这个转折点计算答案。
首先求出剩余树中中间的位置,则左边的树肯定都是沿逆时针走到的,右边的树肯定都是沿顺时针走到的。
然后发现除了最后到达的那棵树,其余树与原点之间的路程都会经过两次,那么前缀和/后缀和优化一下,最终单独减去这个距离即可。
#include<bits/stdc++.h>
#define Tp template<typename Ty>
#define Ts template<typename Ty,typename... Ar>
#define Reg register
#define RI Reg int
#define Con const
#define CI Con int&
#define I inline
#define W while
#define N 200000
#define LL long long
#define Gmax(x,y) (x<(y)&&(x=(y)))
using namespace std;
int n,m,a[N+5];LL pre[N+5],suf[N+5];
int main()
{
RI i,x,t;LL ans=0;for(scanf("%d%d",&m,&n),i=1;i<=n;++i) scanf("%d",a+i);//读入
for(i=1;i<=n;++i) pre[i]=pre[i-1]+a[i];for(i=n;i;--i) suf[i]=suf[i+1]+m-a[i];//前缀和/后缀和
for(i=1;i<=n;++i) x=i+(n-i>>1),Gmax(ans,2*(pre[x]-pre[i-1]+suf[x+1])-(n-i+1&1?a[x]:m-a[x+1]));//逆时针
for(i=n;i>=1;--i) x=(i>>1)+1,Gmax(ans,2*(suf[x]-suf[i+1]+pre[x-1])-(i&1?m-a[x]:a[x-1]));//顺时针
return printf("%lld\n",ans),0;//输出答案
}
\(C\):Coloring Torus(点此看题面)
大致题意: 你可以从\(1\sim 500\)中自选一个\(n\),然后用恰好\(k\)种(\(1\le k\le1000\))颜色给一个\(n\times n\)的正方形染色,使得对于每种相同颜色的格子,它们相邻的格子颜色种类及相应个数完全一致。求一种合法方案。
根据\(k=3\)的小数据,容易产生一个假设,构造方式与对角线有关。
根据\(k\)为偶数的情况,一种构造方式就是第\(i\)行交错填\(2i-1\)和\(2i\),于是开始思考,最终填法会不会也有什么东西是交错填的。
把这两个想法结合在一起,就是交错地在对角线上填。
具体地,例如我们要用\(n\)种颜色给一个\(n\times n\)的正方形染色,在对角线上的构造方式为:
然后如果要用\(2n\)种颜色交错着去填,就变成了这样:
其实交错着填,也就是给偶数列上的数加了个\(n\)。
而且,如果你把这个正方形中任意一个\(n+i\)换成\(i\)(\(1\le i\le n\)),依然合法。
于是,我们只要令\(n=\lceil\frac k4\rceil\times 2\),就可以直接以这种方式构造了。
#include<bits/stdc++.h>
#define Tp template<typename Ty>
#define Ts template<typename Ty,typename... Ar>
#define Reg register
#define RI Reg int
#define Con const
#define CI Con int&
#define I inline
#define W while
#define N 500
using namespace std;
int n,k;
int main()
{
if(scanf("%d",&k),k==1) return puts("1\n1\n"),0;//特判k=1
RI i,j,t;for(printf("%d\n",n=((k+3)/4)*2),i=1;i<=n;++i)//计算n
for(j=1;j<=n;++j) t=i+j-1,t>n&&(t-=n),printf("%d%c",(j&1^1)&&t+n<=k?t+n:t," \n"[j==n]);//若偶数列的数加n不大于k,则加上n
return 0;
}
\(D\):Inversion Sum(点此看题面)
大致题意: 给定一个序列,\(Q\)次操作,第\(i\)次可以选择交换\(a[x_i]\)和\(a[y_i]\)或是不操作。求最后得到的\(2^Q\)种序列的逆序对个数之和。
很容易想到枚举每对数\((x,y)\)(\(a[x]<a[y]\)),设\(f_{i,j,k}\)表示\(i\)次操作之后\(x\)被换到\(j\)、\(y\)被换到\(k\)的方案数,得到一个\(O(n^4Q)\)的大暴力\(DP\)。
然后我们发现,对于每对\((x,y)\)都去\(DP\)一遍实际上是完全没有必要的,因为\(DP\)转移并不会因为初值的改变而改变,所以只要初始化\(f_{0,x,y}=[a[x]<a[y]]\),就得到了一个\(O(n^2Q)\)的升级做法。
接着让我们来看看转移方程:
发现,每次只有\(O(n)\)种状态(有至少一维等于\(x\)或\(y\)的状态)需要特殊转移,其余的状态都是乘以\(2\)。
那么根据套路,我们可以给\(f_{i,j,k}\)除以\(2^i\),每次\(DP\)数组直接继承前一次的数组,并在最后给答案乘上\(2^Q\)。
此时的转移方程为:
于是就得到了一个优秀的\(O(Qn)\)的\(DP\),这道题也就做完了。
#include<bits/stdc++.h>
#define Tp template<typename Ty>
#define Ts template<typename Ty,typename... Ar>
#define Reg register
#define RI Reg int
#define Con const
#define CI Con int&
#define I inline
#define W while
#define N 3000
#define X 1000000007
#define I2 500000004
using namespace std;
int n,m,a[N+5],f[N+5][N+5];
int main()
{
RI i,j,x,y;for(scanf("%d%d",&n,&m),i=1;i<=n;++i) scanf("%d",a+i);
for(i=1;i<=n;++i) for(j=1;j<=n;++j) a[i]<a[j]&&(f[i][j]=1);//赋初值
for(i=1;i<=m;++i)//枚举操作
{
scanf("%d%d",&x,&y),f[x][y]=f[y][x]=1LL*I2*(f[x][y]+f[y][x])%X;//DP转移
for(j=1;j<=n;++j) j^x&&j^y&&(f[x][j]=f[y][j]=1LL*I2*(f[x][j]+f[y][j])%X);
for(j=1;j<=n;++j) j^x&&j^y&&(f[j][x]=f[j][y]=1LL*I2*(f[j][x]+f[j][y])%X);
}
RI ans=0;for(i=1;i<=n;++i) for(j=1;j^i;++j) ans=(ans+f[i][j])%X;//统计答案
for(i=1;i<=m;++i) ans=2LL*ans%X;return printf("%d\n",ans),0;//乘上2^m
}
\(E\):Less than 3(点此看题面)
大致题意: 给定两个长为\(n\)的\(01\)串\(s,t\),每次你可以取反\(s\)中的某一位,要求任意时刻都不能存在连续三个相同的字符。问至少经过多少次转化能够让\(s\)变成\(t\)。
非常神仙的操作,考虑我们在每对相邻的\(01\)之间画一条红线,每对相邻的\(10\)之间画一条蓝线,如图所示:
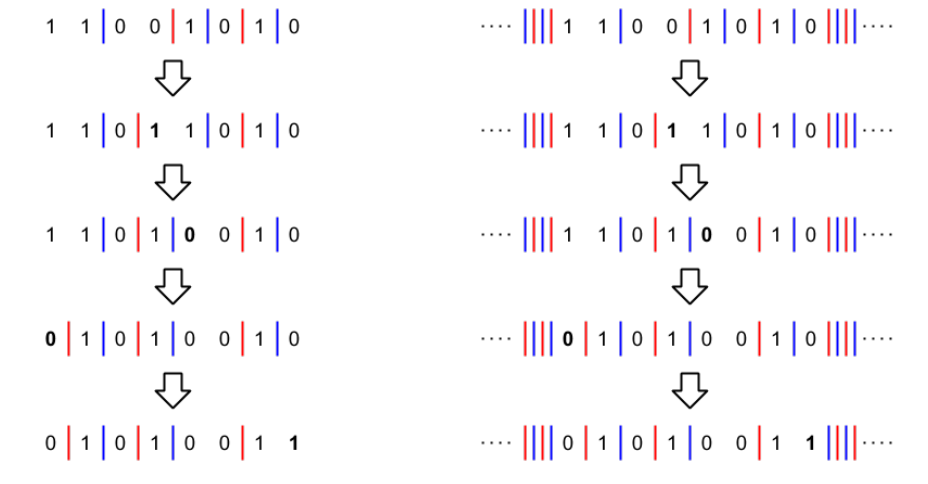
考虑一次操作如果不是在边界上执行,必然只会导致线的移动。
否则,可能会产生一条新线或是删去一条原有的线。(可看作从外部移入一条线,或是把一条线移出局)
因为不可能从中间冒出一条线,那么我们只要枚举\(s\)中第一条红线与\(t\)中第\(i\)条红线配对,或是\(s\)中第\(i\)条红线与\(t\)中第一条红线配对,找出其中的最小步数即可。

不难发现红线与蓝线的情况可以独立讨论,直接把这一过程进行两次就行了。
注意,没有线的情况(只可能出现在\(n\le2\)时)要特判。
#include<bits/stdc++.h>
#define Tp template<typename Ty>
#define Ts template<typename Ty,typename... Ar>
#define Reg register
#define RI Reg int
#define Con const
#define CI Con int&
#define I inline
#define W while
#define N 5000
using namespace std;
int n,ans,t1,t2,a1[N+5],a2[N+5];char s1[N+5],s2[N+5];
I void Calc()//计算答案
{
RI i,j,Mn=1e9,res;for(i=1;i<=t2;++i)//枚举s中第一条红线与t中第i条红线配对
{
for(res=0,j=1;j^i;++j) res+=a2[j];//前面的红线
for(j=i;j-i+1<=t1&&j<=t2;++j) res+=abs(a1[j-i+1]-a2[j]);//配对的红线
W(j-i+1<=t1) res+=n-a1[j-i+1],++j;W(j<=t2) res+=n-a2[j],++j;Mn=min(Mn,res);//后面的红线
}
for(i=1;i<=t1;++i)//枚举s中第i条红线与t中第一条红线配对,具体过程同上
{
for(res=0,j=1;j^i;++j) res+=a1[j];
for(j=i;j<=t1&&j-i+1<=t2;++j) res+=abs(a1[j]-a2[j-i+1]);
W(j<=t1) res+=n-a1[j],++j;W(j-i+1<=t2) res+=n-a2[j-i+1],++j;Mn=min(Mn,res);
}ans+=Mn;
}
int main()
{
RI i;if(scanf("%d%s%s",&n,s1+1,s2+1),n==1) return putchar(48|(s1[1]^s2[1])),0;//特判n=1时没线的情况
if(n==2&&s1[1]==s1[2]&&s2[1]==s2[2]) return putchar(48+2*(s1[1]^s2[1])),0;//特判n=2时没线的情况
for(t1=0,i=1;i^n;++i) s1[i]=='0'&&s1[i+1]=='1'&&(a1[++t1]=i);//连红线
for(t2=0,i=1;i^n;++i) s2[i]=='0'&&s2[i+1]=='1'&&(a2[++t2]=i);Calc();//求答案
for(t1=0,i=1;i^n;++i) s1[i]=='1'&&s1[i+1]=='0'&&(a1[++t1]=i);//连蓝线
for(t2=0,i=1;i^n;++i) s2[i]=='1'&&s2[i+1]=='0'&&(a2[++t2]=i);Calc();//求答案
return printf("%d\n",ans),0;//输出答案
}
\(F\):Permutation and Minimum(点此看题面)
大致题意: 给定一个\(1\sim 2n\)的排列\(a_i\),其中有一些位置是\(-1\)。定义\(b_i=\min\{a_{2i-1},a_{2i}\}(1\le i\le n)\),让你把排列填充完整,问有多少种可能的\(b\)。
以下是一个我自己想出来的有些复杂的\(DP\),更简单的\(DP\)可以去看\(bzt\)神仙的博客AtCoder Grand Contest 030题解。
考虑我们从小到大枚举填\(i\),如果填在一个还未填过的\((-1,-1)\)对或者满足\(i<x\)的\((x,-1)\)对中可以使\(b\)发生变化,否则无影响。
因此设\(f_{i,j,k}\)表示当前填到了\(i\),\((-1,-1)\)对已经填过\(j\)个,满足\(i<x\)的\((x,-1)\)对已经填过\(k\)个。
转移要分三大类:
第一种情况,\(i\)出现在某个\((x,y)\)对中,无影响,直接转移。
第二种情况,\(i\)出现在某个\((x,-1)\)对中,看似仍旧无影响,但实际上之后满足\(i<x\)的\((x,-1)\)对个数会减少\(1\)。
因此要转移\(f_{i,j,k}\),我们需要判断当前少掉的这个\((x,-1)\)对在之前是否填过:(假设\(h\)为少掉当前这对之前的\((x,-1)\)对数)
- 若它不包含,则相当于从\(h-1\)个数中选择了\(k\)个数,而总方案是从\(h\)个数中选择了\(k\)个数。
- 若它包含,则相当于从\(h-1\)个数中选择了\(k\)个数,而总方案是从\(h\)个数中选择了\(k+1\)个数。
注意,这个组合数作为系数转移看起来很恶心(也确实很恶心),但实际上是我写复杂了,只要把数对看成无序的,在最后乘上一个阶乘,就可以去掉转移过程中的组合数。
第三种情况,\(i\)没有出现过,那么分三种转移:
- \(i\)填在了某个无影响的地方。
- \(i\)填在了某个还未填过的\((-1,-1)\)对中。
- \(i\)填在了某个满足\(i<x\)的\((x,-1)\)对中。
后两种的方案数是显然的,因此只要考虑如何判断第一种情况是否能转移。
假设\(t\)为总\((-1,-1)\)对数,\(g\)为总\((x,-1)\)对数,\(h\)为满足\(x<i\)的\((x,-1)\)对数,\(cnt\)为之前填过的数的个数。
则\(cnt-j-k\)为已经填完的无影响的对数,\(j+g-h\)是总共的无影响的对数,那么只要\((j+g-h)-(cnt-j-k)>0\)就可以转移了。
#include<bits/stdc++.h>
#define Tp template<typename Ty>
#define Ts template<typename Ty,typename... Ar>
#define Reg register
#define RI Reg int
#define Con const
#define CI Con int&
#define I inline
#define W while
#define N 300
#define X 1000000007
using namespace std;
int n,p[2*N+5],s[2*N+5],C[2*N+5][2*N+5],IC[2*N+5][2*N+5],f[2*N+5][N+5][N+5];
I int QP(RI x,RI y) {RI t=1;W(y) y&1&&(t=1LL*t*x%X),x=1LL*x*x%X,y>>=1;return t;}
int main()
{
RI i,j;for(C[0][0]=IC[0][0]=i=1;i<=2*N;++i)//组合数
for(C[i][0]=IC[i][0]=j=1;j<=i;++j) C[i][j]=(C[i-1][j-1]+C[i-1][j])%X,IC[i][j]=QP(C[i][j],X-2);
RI k,x,y,t=0,g=0;for(scanf("%d",&n),i=1;i<=n;++i)//读入同时统计
{
if(scanf("%d%d",&x,&y),~x&&(p[x]=1),~y&&(p[y]=1),~x&&~y) continue;
~x&&(s[x]=1,++g),~y&&(s[y]=1,++g),!~x&&!~y&&++t;
}
RI tmp,cnt=0,h=g;for(f[0][0][0]=i=1;i<=2*n;++i)//枚举填数
{
if(s[i])//如果出现在(x,-1)对中
{
for(j=0;j<=t;++j) for(k=0;k^h;++k) f[i][j][k]=
(1LL*C[h-1][k]*IC[h][k]%X*f[i-1][j][k]+1LL*C[h-1][k]*IC[h][k+1]%X*f[i-1][j][k+1])%X;
--h;continue;
}
if(p[i]) {for(j=0;j<=t;++j) for(k=0;k<=h;++k) f[i][j][k]=f[i-1][j][k];continue;}//如果出现在(x,y)对中
for(j=0;j<=t;++j) for(k=0;k<=h;++k)
(tmp=(j+g-h)-(cnt-j-k))>0&&(f[i][j][k]=f[i-1][j][k]),//能转移才转移
j&&(f[i][j][k]=(1LL*(t-j+1)*f[i-1][j-1][k]+f[i][j][k])%X),//填(-1,-1)对
k&&(f[i][j][k]=(1LL*(h-k+1)*f[i-1][j][k-1]+f[i][j][k])%X);//填(x,-1)对
++cnt;//记录填过的数的个数
}
RI ans=0;for(j=0;j<=t;++j) ans=(ans+f[2*n][j][0])%X;return printf("%d\n",ans),0;//统计答案并输出
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号