JZ69【动态规划】斐波那契数列和青蛙跳台阶

 

 

 

描述

一只青蛙一次可以跳上1级台阶，也可以跳上2级。求该青蛙跳上一个 n 级的台阶总共有多少种跳法（先后次序不同算不同的结果）。

 

数据范围：1≤n≤40

要求：时间复杂度：O(n)O(n) ，空间复杂度： O(1)O(1)

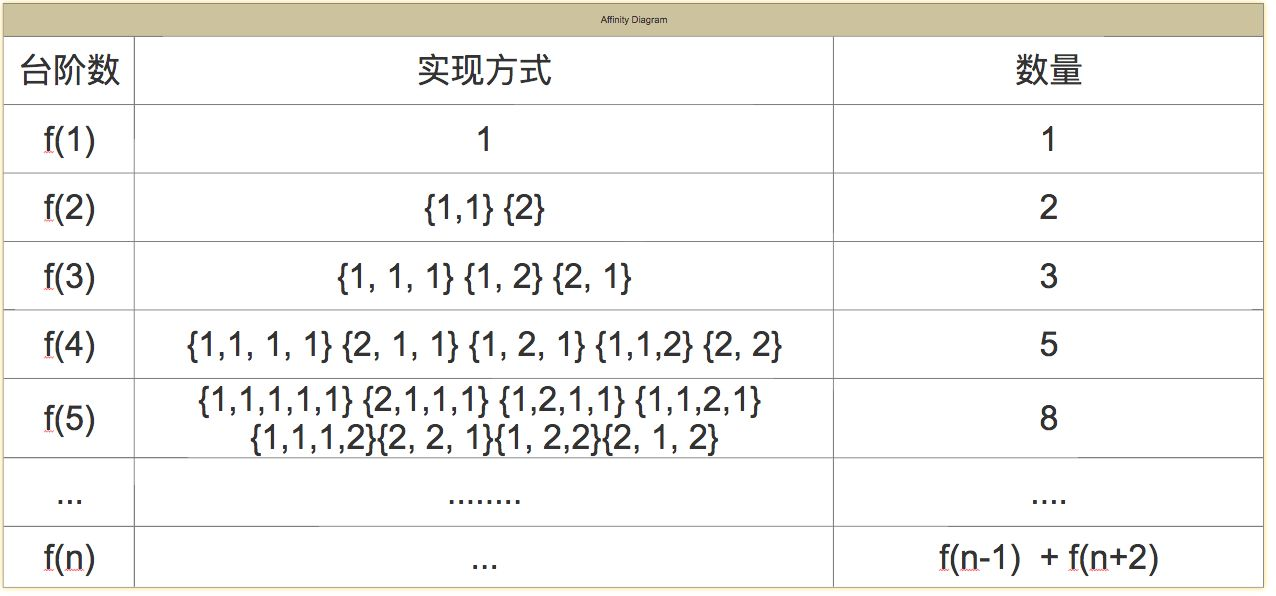
解决方法：
可以转化为斐波那契数列的方式进行求解，假设要跳N阶台阶，那么第一步有两种跳法：
（1）跳一步，后面还有n-1个台阶需要跳；
（2）跳两步，后面还有n-2个台阶需要跳。
可以看到跳n阶台阶的跳法数等于跳n-1和n-2阶台阶数的和，即f(n) = f(n-1) + f(n-2)

求解方式：
（1）递归，代码很简洁，但不推荐此方式，有大量的重复计算

class Solution:
    def jumpFloor(self , number: int) -> int:
        if number in (1,2):
            return number
        while numbers>2:
            return jumpFloor(number-1)+jumpFloor(number-2)

 

（2）从下往上计算，很简单的动态规划，时间复杂度为0（n）,通常软件中采用这种写法。