第1章 第2节：一、数列的极限的定义
1.数列：
x1,x2,x3.......xn，就叫做数列，记作 { xn }
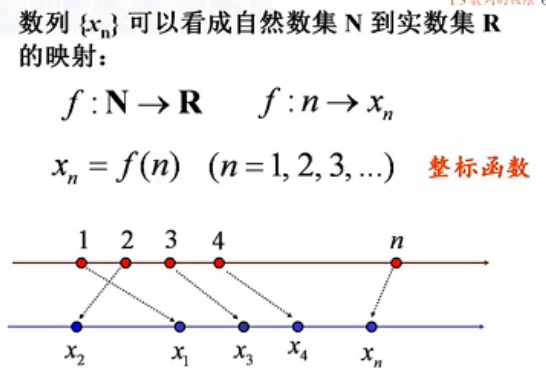
2.一般项：
x1,x2,x3.......xn中的 xn ，
例如：1/2,2/3,3/4……n/n+1，中的n/n+1就是一般项
a、b两个数接近程度思路： | b - a | 得到数值越小越接近
3.数列极限定义：
设｛xn｝为数列，若存在常数a，对给定任意数ε(无论它多小)，总存在正数N，使得当n>N时，不等式：
| xn-a | < ε 都成立，
则称常数a是数列 { xn }的极限 或 称数列 ｛Xn｝收敛于a，记为：
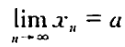或 xn→a （n→∞）
如不存在这样数a：则说数列的极限不存在， 或 数列是发散的 或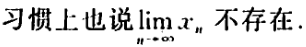 
【定义理解：】
例如：数列｛1/x｝，它常数是 a=0，给定任意数 ε=0.1，则正数N=10，此时只要 n >10【n取任一个数：11好了】，不等式即成立：| 1/11-0 | < 0.1
4.数列｛xn｝极限为a几何解释：
在数轴上做点a图即开区间n的ε领域：（a-ε，a+ε）如下图：
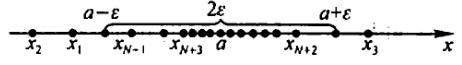
又不等式 | xn-a | < ε 与 a-ε < xn < a+ε 等价，所以 n>N 时，所有 xn 点都落在（a-ε，a+ε）内，只有有限个点落在区域外（最多N个）。
用符号表示：
<=> ∃ 正整数 N，当 n>N 时，有 | xn-a | < ε
5.例题：
例1：证明数列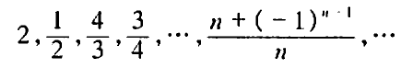
极限是1.
证明：
以下是视频
1.数列有界性：
习题：
