同济:004.三角函数(1.1映射与函数)
(4)三角函数(Trigonometric Function)
|
基本函数
|
英文
|
缩写
|
表达式
|
语言描述
|
|
|
sine
|
sin
|
a/c
|
∠A的对边比斜边
|
||
|
cosine
|
cos
|
b/c
|
∠A的邻边比斜边
|
||
|
tangent
|
tan
|
a/b
|
∠A的对边比邻边
|
||
|
cotangent
|
cot
|
b/a
|
∠A的邻边比对边
|
||
|
secant
|
sec
|
c/b
|
∠A的斜边比邻边
|
||
|
cosecant
|
csc
|
c/a
|
∠A的斜边比对边
|
(注:正切函数、余切函数曾被写作tg、ctg,现已不用这种写法)
基本三角函数关系的速记方法
1)对角相乘乘积为1,即sinθ·cscθ=1; cosθ·secθ=1; tanθ·cotθ=1。
2)六边形任意相邻的三个顶点代表的三角函数,处于中间位置的函数值等于与它相邻两个函数值的乘积,如:sinθ=cosθ·tanθ;tanθ=sinθ·secθ...
3)阴影部分的三角形,处于上方两个顶点的平方之和等于下顶点的平方值,如:



关系:

变化规律:
- 正弦值在
 随角度增大(减小)而增大(减小),在
随角度增大(减小)而增大(减小),在  随角度增大(减小)而减小(增大);
随角度增大(减小)而减小(增大);
- 余弦值在
 随角度增大(减小)而增大(减小),在
随角度增大(减小)而增大(减小),在  随角度增大(减小)而减小(增大);
随角度增大(减小)而减小(增大);
- 正切值在
 随角度增大(减小)而增大(减小);余切值在
随角度增大(减小)而增大(减小);余切值在  随角度增大(减小)而减小(增大);
随角度增大(减小)而减小(增大);
- 正割值在
 随着角度的增大(或减小)而增大(或减小);
随着角度的增大(或减小)而增大(或减小); - 余割值在
 随着角度的增大(或减小)而减小(或增大)。
随着角度的增大(或减小)而减小(或增大)。 - 注:π/2表示弧度=1/4圆弧=90度
- 注2:弧度换算成角度(把π换成180度代入即可)如:π/2=180/2=90
函数图:
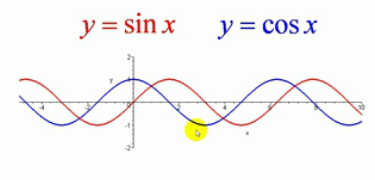
sinx:奇函数,定义域:一切实数R,值域[-1,1];周期派;
cosx:偶函数,其它同上
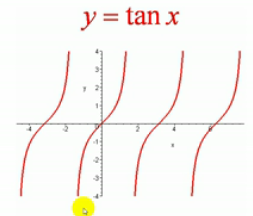
tanx:周期派
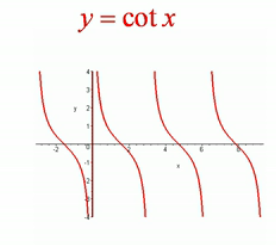
cotx:周期派
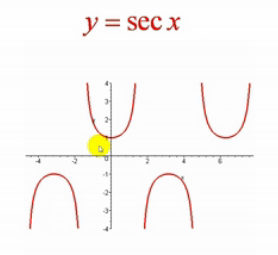
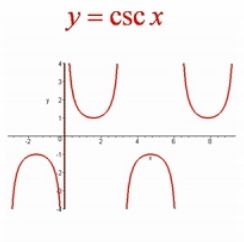
反三角函数(Inverse Trigonometric Function)
1.sinx反函数(arcsinx)
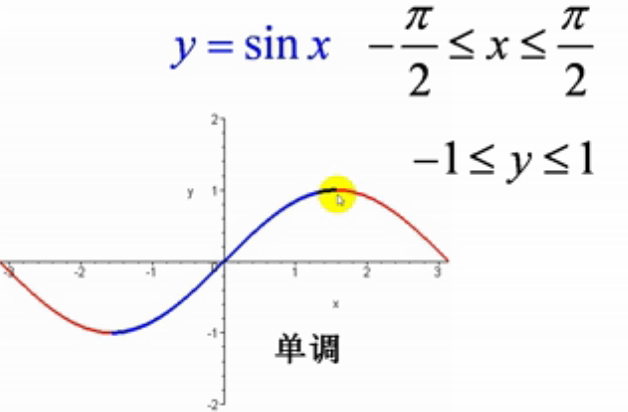
如上图:sin x 不是单调函数,所以它整体没有反函数;
但在 [ -90度,90度 ] 即 [ -π/2,π/2 ],是单调的,可以求此区间反函数;

y=sin x => x = arc sin y
arc代表:当前函数的反函数
反函数图:
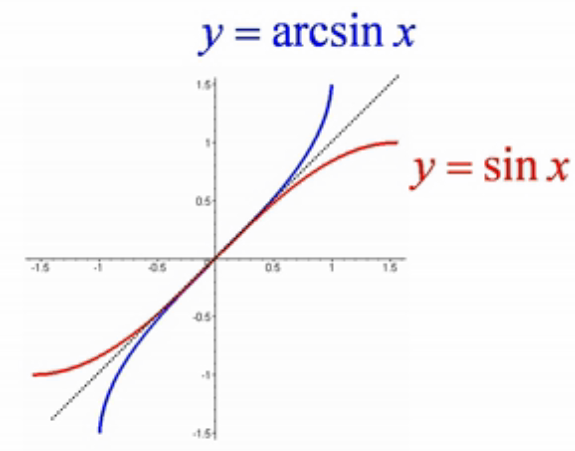
sinx和arc sin x 关于 y=x 对称
2.cosx反函数:
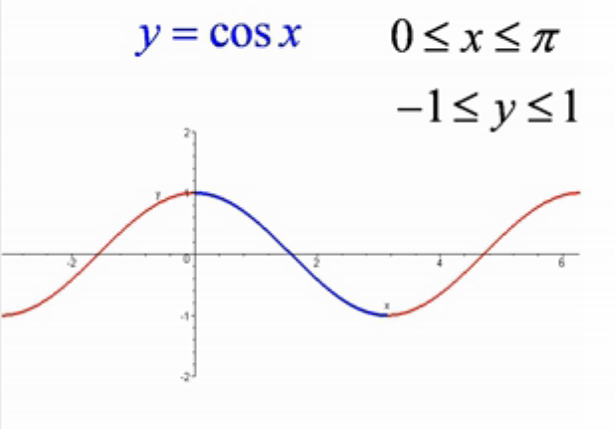
如图:cosx整体不是单调的,但在0-180 [ 0-π ]度是单调的,值介于[-1,1],可求此区间反函数
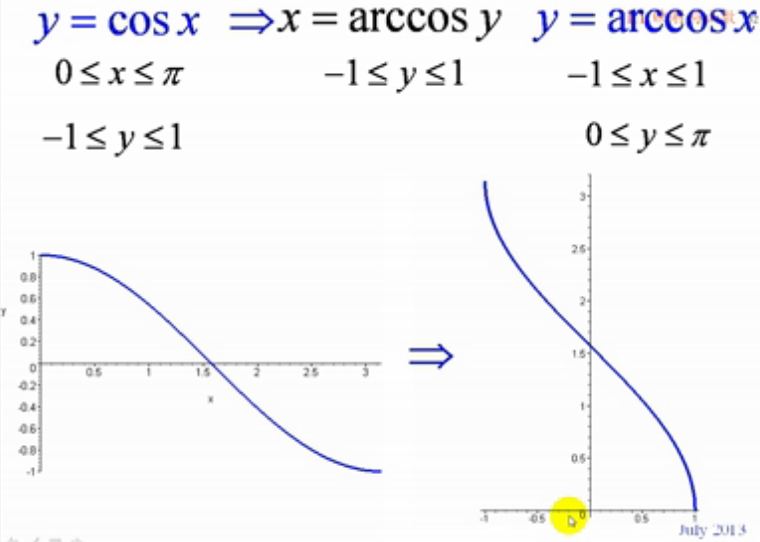
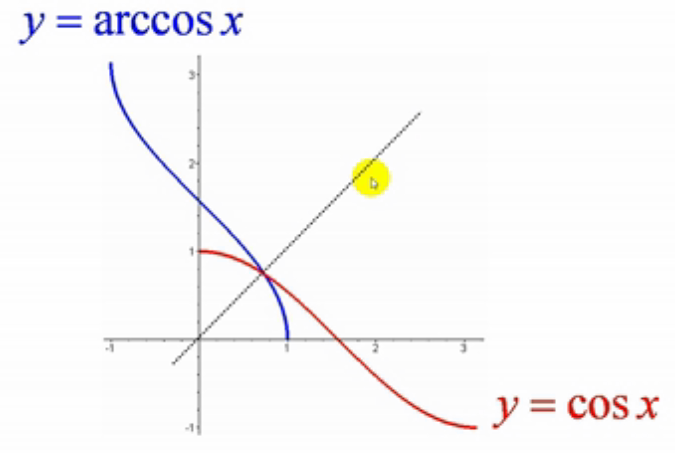
如上图:cosx和其反函数关于y=x对称
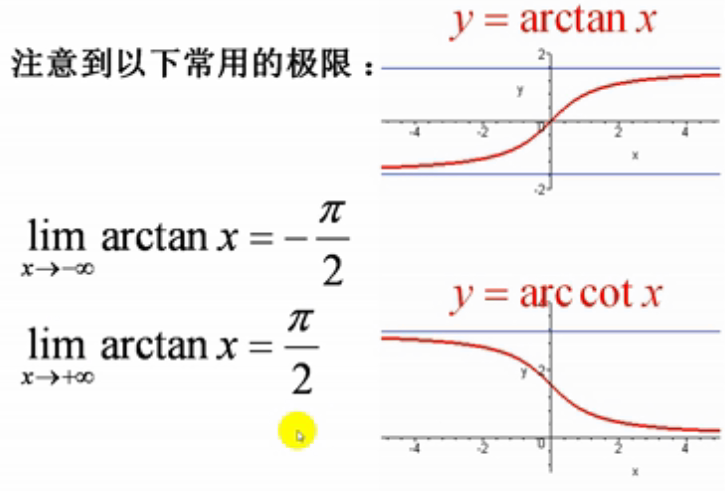
3.tanx反函数
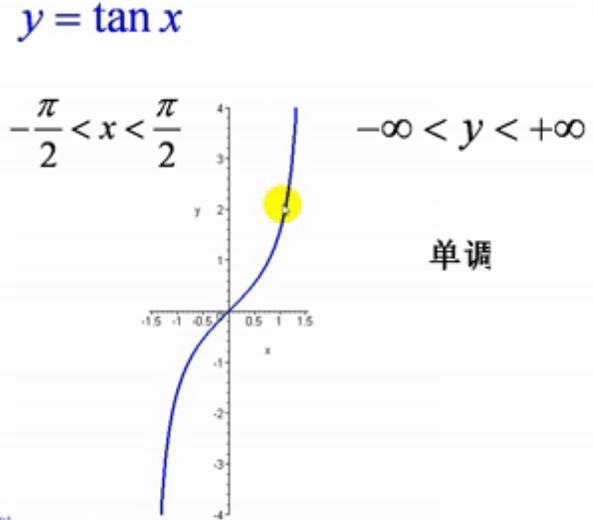
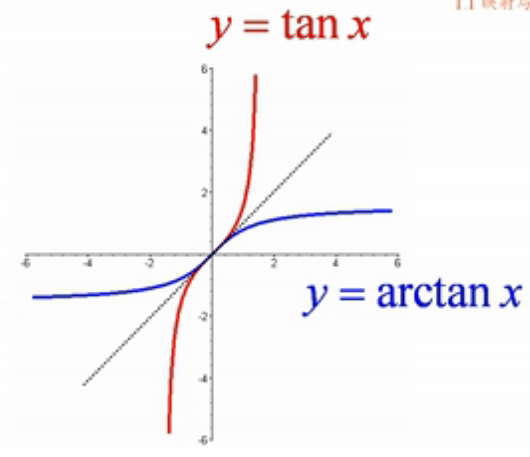
如上图:它在(0,π/2)上单调递增至正无穷大
推导值域Rf,定义域Df,过程

对称性:
4.cotx反函数
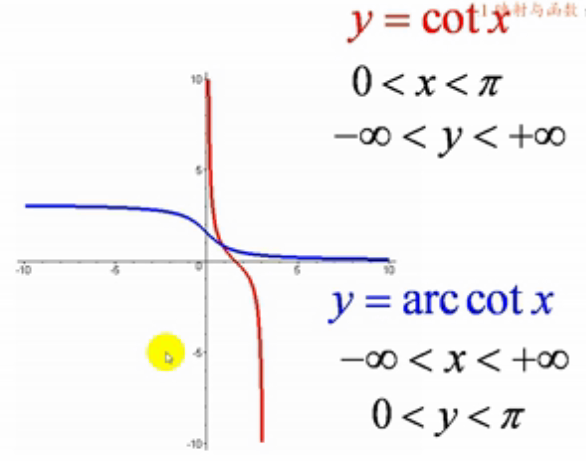
(高数学习手册 P21)
以上四个反三角函数都是有界函数:
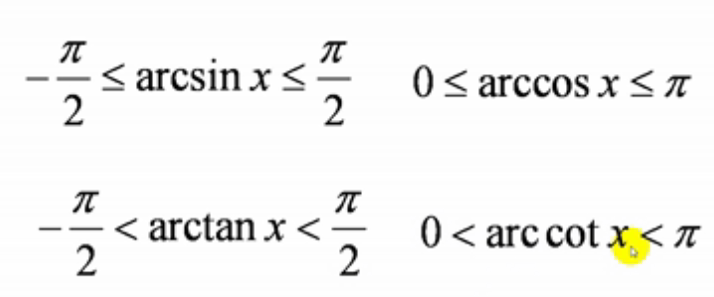








【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· AI与.NET技术实操系列:基于图像分类模型对图像进行分类
· go语言实现终端里的倒计时
· 如何编写易于单元测试的代码
· 10年+ .NET Coder 心语,封装的思维:从隐藏、稳定开始理解其本质意义
· .NET Core 中如何实现缓存的预热?
· 分享一个免费、快速、无限量使用的满血 DeepSeek R1 模型,支持深度思考和联网搜索!
· 基于 Docker 搭建 FRP 内网穿透开源项目(很简单哒)
· ollama系列01:轻松3步本地部署deepseek,普通电脑可用
· 25岁的心里话
· 按钮权限的设计及实现