集合对偶律：分别用图文证明

集合几个法则：

求证：

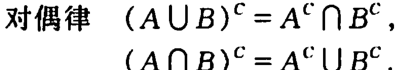
注：右上角C表示此集合的补集/余集

语言描述：A 并 B的补集 = A的补集 交  B的补集

　　　　　A交B的补集 = A的补集 并 B的补集

文字证明：（思路：证明两个集合相等，可证两集合互为子集）

 

用图证明：

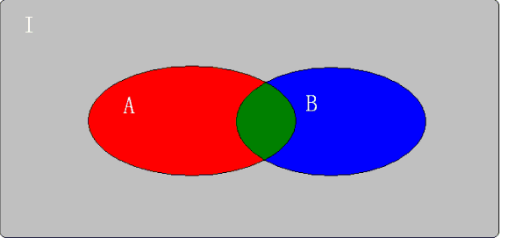
首先,整个 I 区域被 A、B 分割为互不重叠的 4 部分：灰、红、蓝、绿；

而对偶律,也就是下面这个公式,可以这样证明：

式1：左=（红绿 并 蓝绿）的补 =灰

　　  右= 红绿的补 交 蓝绿的补 = 灰蓝 交 灰红=灰

所以……

==============================================================

式2：左=（红绿 交 蓝绿）的补 =灰红蓝

         右=红绿的补 并 蓝绿的补 =灰蓝 并 灰红=灰红蓝

所以……