同济：003.映射与函数3
函数几种特性：
- 有界性
- 单调性
- 奇偶性
- 周期性
- 2-4为高中学习自己复习（高数同济P12-14）
1.有界性（Bounded function）
应写为：设有集合 X ，它在f(x)函数的定义域内，称函数f(x)在集合X 上有界，如存在M>0，则有：
| f(x) | <= M (∀ x ∈ X)
或
-M <= f(x) <= M (∀ x ∈ X)
1.1有界性示意图：
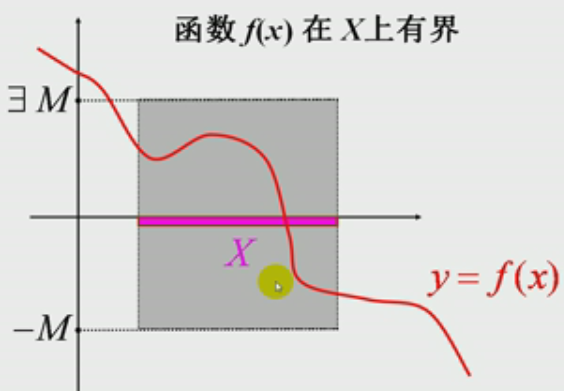
2. 无界：即非有界
∀ M>0,∀ x ∈ X ,| f(x) | > M
3.有界无界对比
区别：
- 有界：...任意x...<=M
- 无界：...存在x... >M
4.上界和下界
例题：
17:41
例：
图：
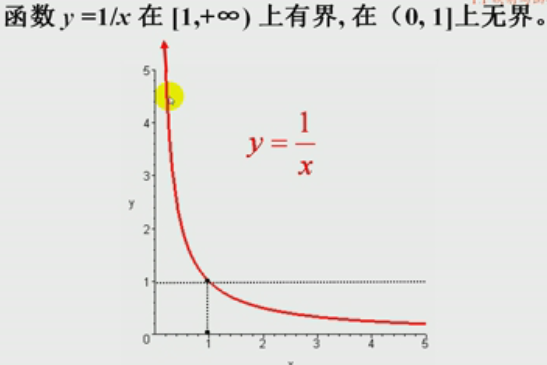
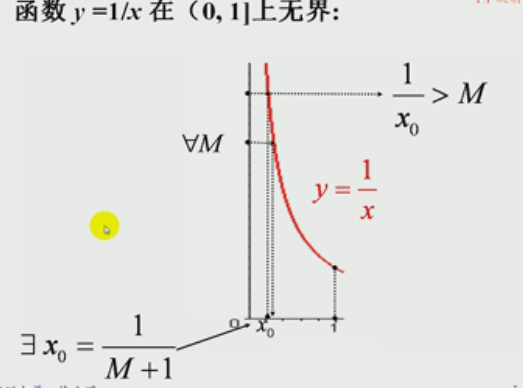
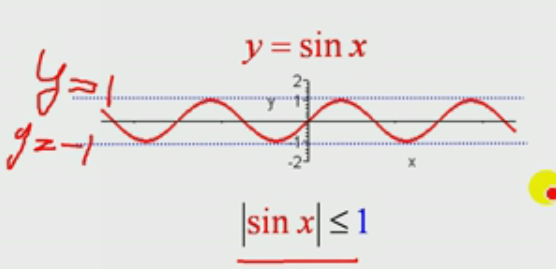
常见有界函数
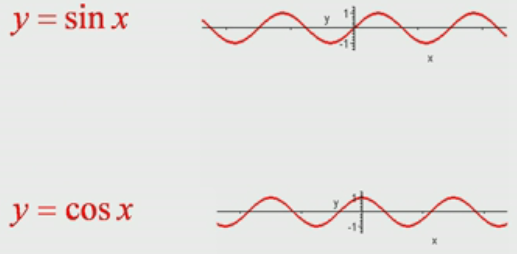
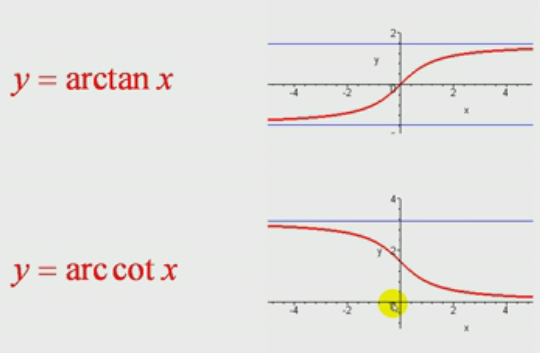
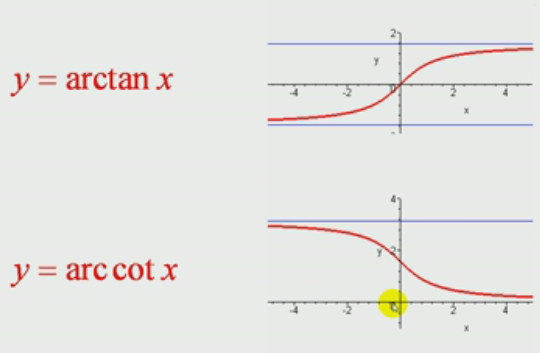
arc:取函数的反函数
arc tan x：反正切函数
arc cot x：反余切函数
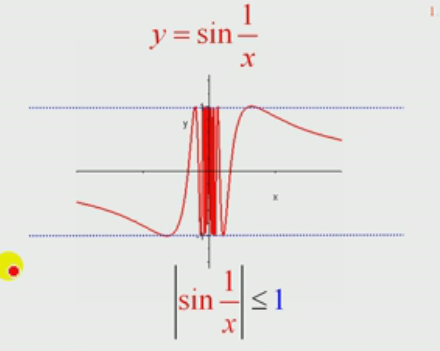
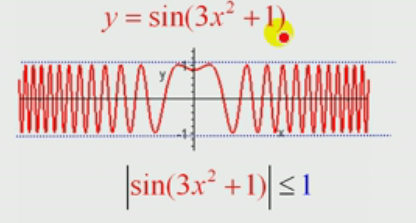
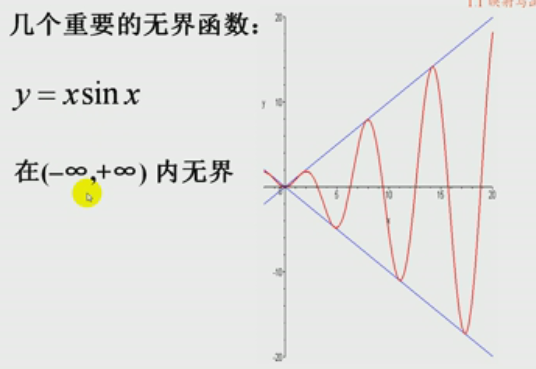
无界函数示例
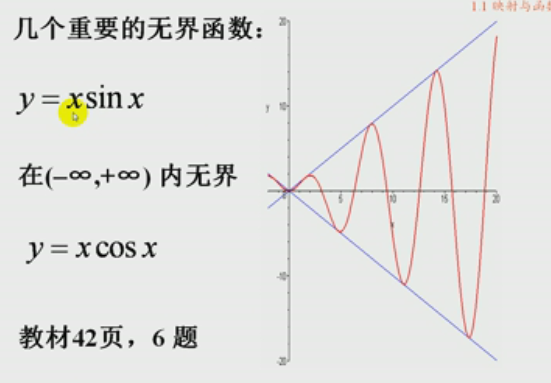
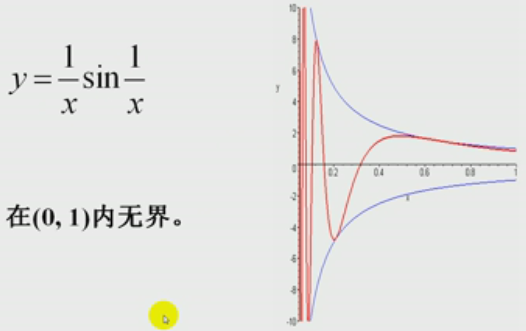
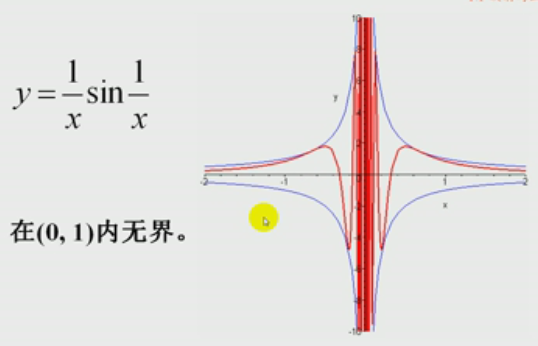
自学部分：
奇怪函数：狄利克雷函数（dirichlet function）
性质：
影响：
意义
函数的复合：
几种初等函数：
1.幂函数（power function）
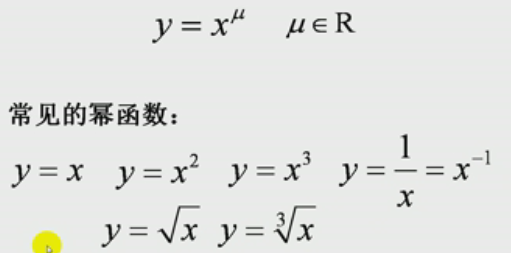
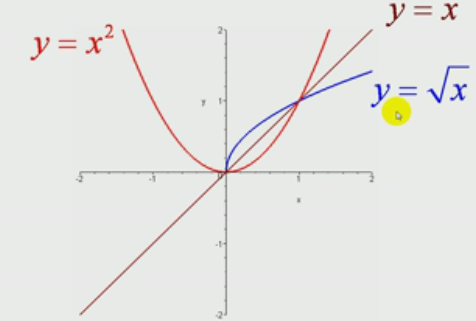
定义域（Dy）：一切非负数
值 域（Ry）：一切非负数
y=x^2是偶函数；
y=x是奇函数；
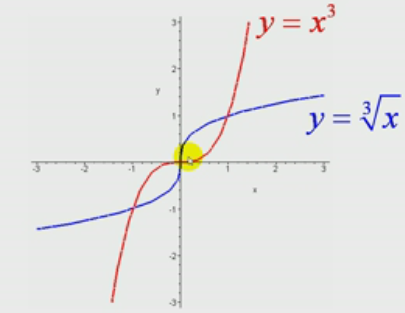
关于y=x直线对称；
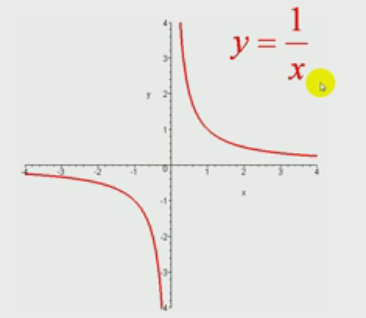
定义域Dy：除原点外一切实数
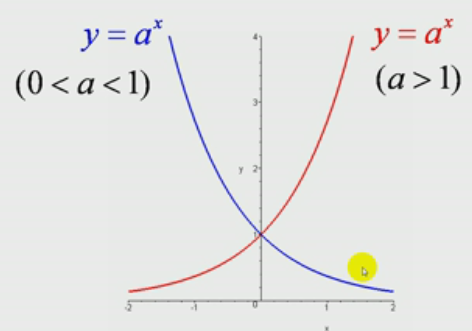
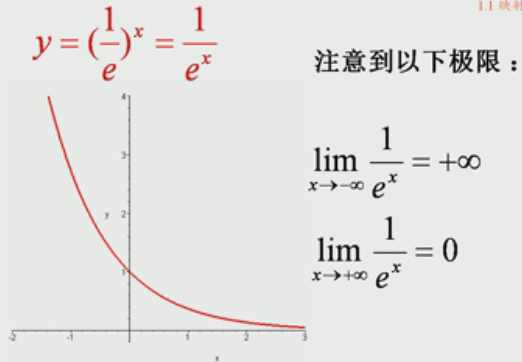
指数函数（Exponential function）：
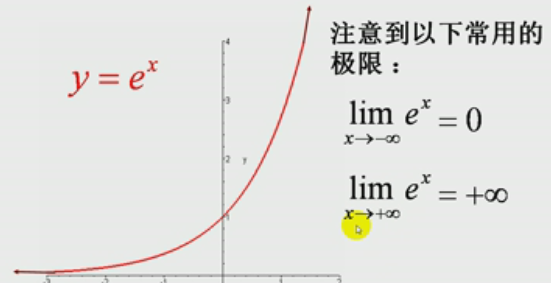
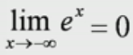表示：（lim表示极限）即 函数x取值 趋于负无穷大时，函数值趋于0；
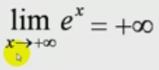表示：（lim表示极限）即 函数x取值 趋于正无穷大时，函数值趋于正无穷大；
对数函数（Logarithmic function）：
它是指数函数反函数
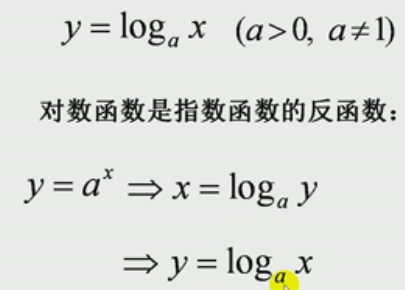
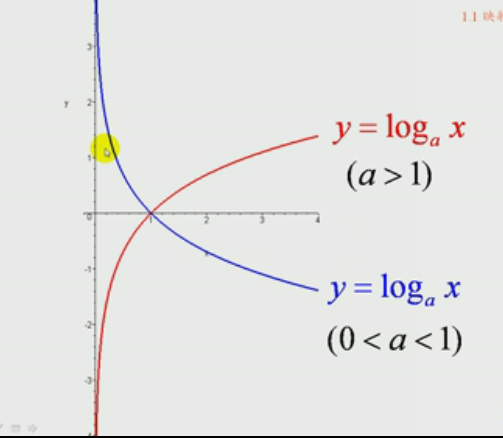
常见对数函数：（a > 1）
遇到非e为底的对数，可用换底公式转化成e为底对数
记住lnx图形：下图
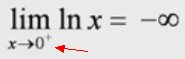表示：正方向趋于0
2019-05-18 09:53:12
