同济：001 函数基础概念：邻域、映射相关

001讲-徐小湛

1.差集：A \ B = { x | x ∈ A 且 x ∉ B }

逻辑量词符号表示：

2.“任意”：  ∀

例：∀ a,b ∈ R，且a<b（任意实数a,b 且 a<b）

3.“存在”：∃

例：

 

4.邻域：（点x0的邻居区域）

 

U(X0，δ)={x |  |X-X0|<δ}

　　　　={x| X0-δ < x <x0+δ}

　　　　=(x0-δ,x0+δ)

例：求2的0.1邻域

U(2,0.1)={x| |x-2|<0.1}

　　　　=( 2-0.1,2+0.1)

　　　　=(1.9,2.1)

5.去心邻域：（即邻域去掉中心X0）

 

6.映射概念（映射是一个规则）：

设 X，Y是集合；

∀ x ∈ X，∃唯一y∈Y，使：

f: x→y

则称：f为X到Y一个映射

记： y=f(x)

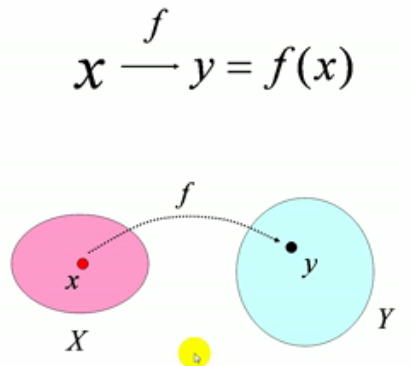（映射图示）

7.映射相关概念：

8.之间关系：

 

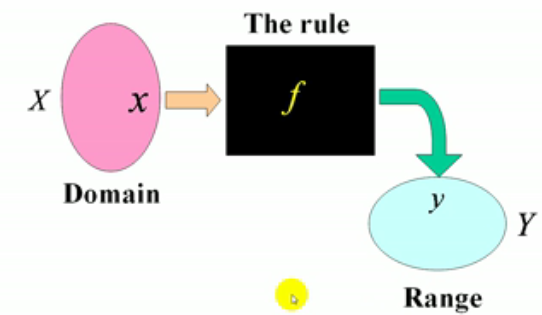
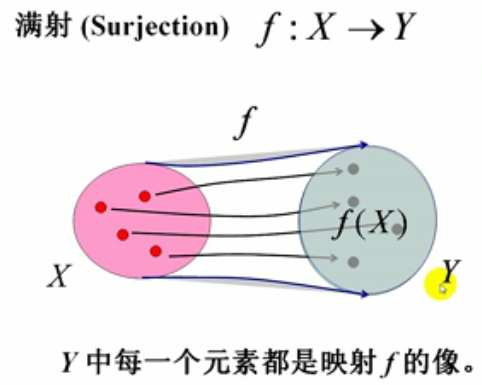
9.满射：（Y中每个元素都是映射f的像）

 

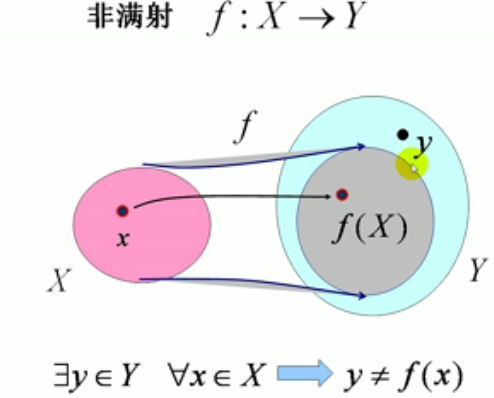
10.非满射：（Y中至少有一个不是映射f的像）

 

 

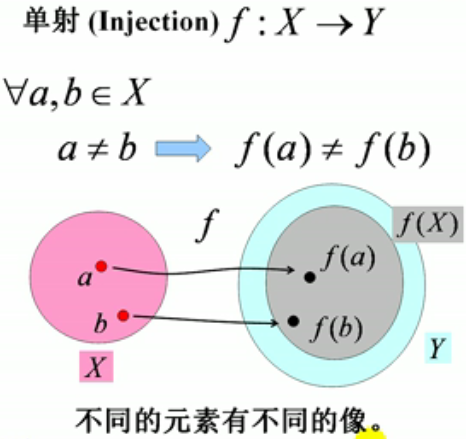
11.单射：集合X中任意两数a≠b，映射在集合Y中的像 f(a)≠f(b)

 

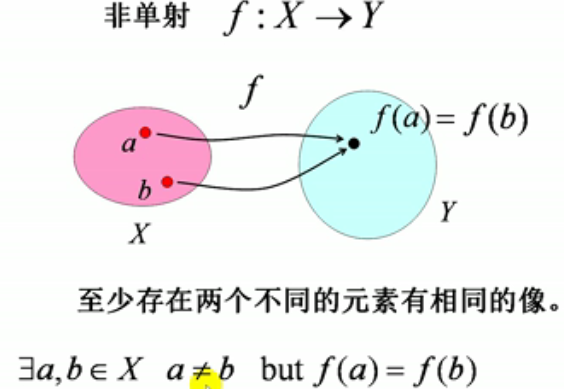
12.非单射：集合X中至少存在两个不同元素a≠b  通过f映射在   集合Y中有相同的像，即f(a)=f(b)

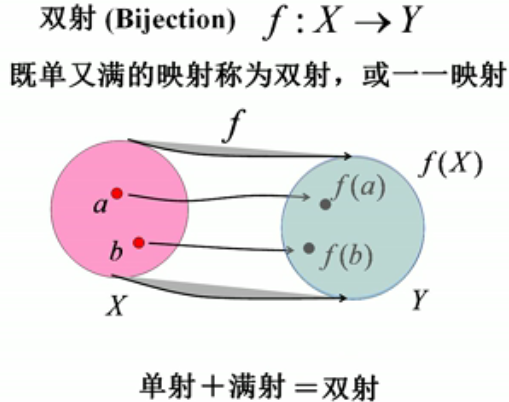
13.双射：即是单射，又是满射 称双射

 

 

14.题要：单射很重要

14-1.每个单射都可以诱导一个双射

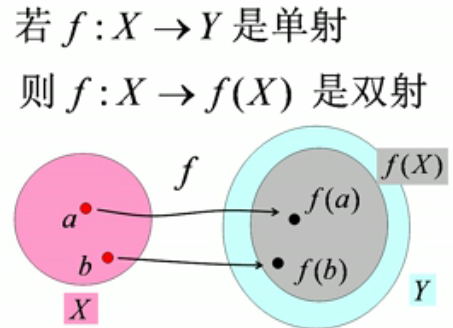
14-2.每个单射都可诱导一个逆映射

 

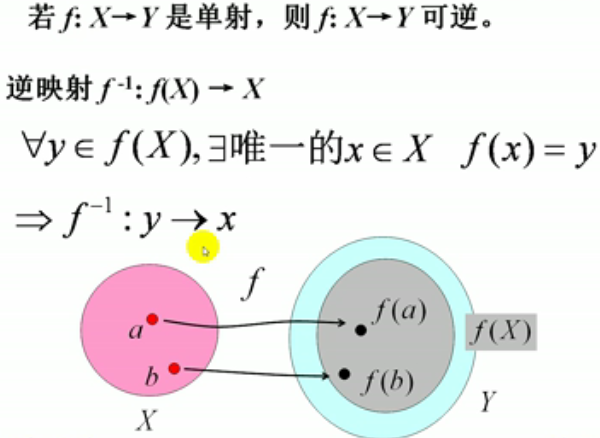
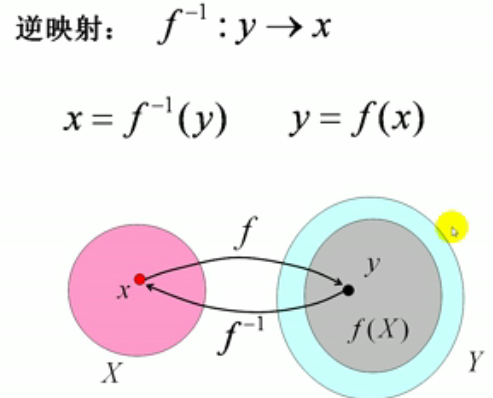
15.【逆映射】：集合Y到X的逆运算

 

==========（三）函数=============

1.函数概念：函数是一种特殊映射

 

 2.函数相关概念（同映射）

 

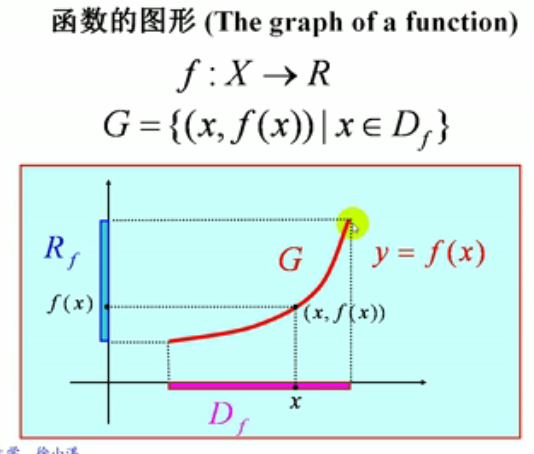
3.函数的图形

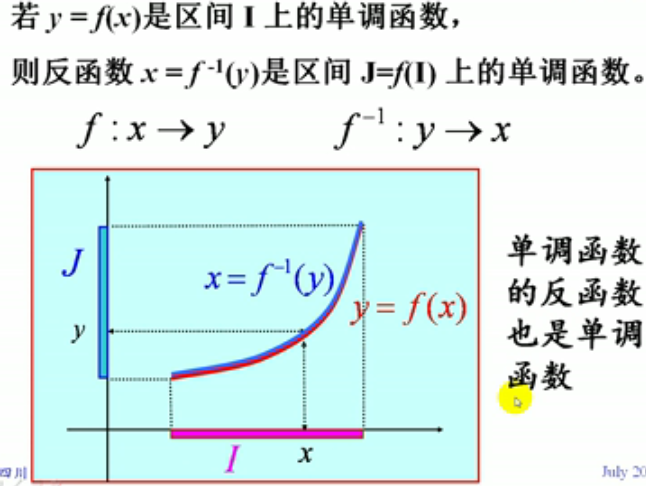
4.反函数：即逆映射

5.单调函数

【单调函数定义】设x1>x2,如果在一个区间内都保持f（x1）>f(x2) 或 f(x1)<f(x2)，那我们就说在此区间他是属于单调函数了

 

 6.一个函数有反函数条件是什么？

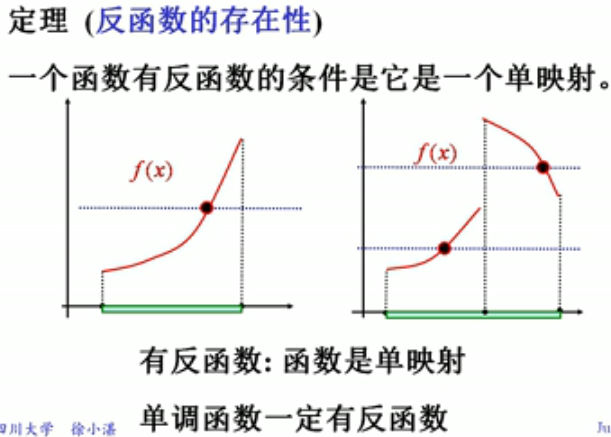
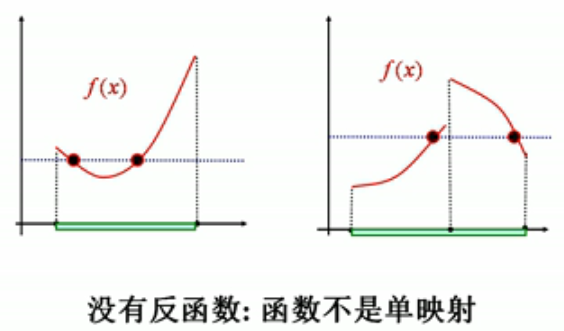
6.1 非单射函数没有反函数示例如下：(同一个Y对应两个x)