图与搜索
- 图是什么
图,顾名思义,就是一张大大的网,网中的每个节点都与另外一个节点直接或者间接的联系。互联网就是一个大大的图,从A到B到C经过的路由,就是图的搜索算法。
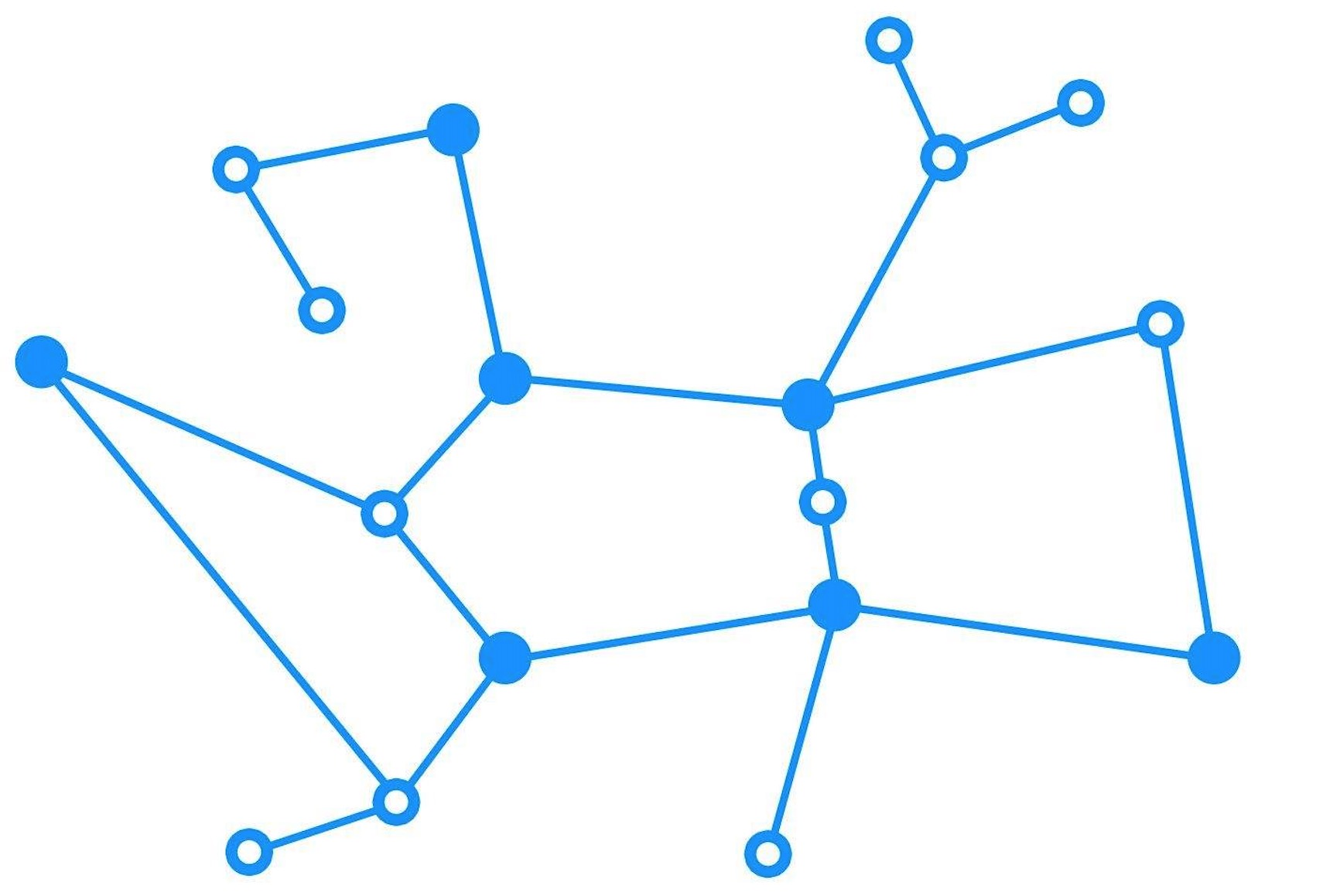
要给图下一个定义,那就是在众多离散节点中可以产生回路的数据结构。比之线性数据结构的单线特性,树形结构的多路分叉特性,图的最大特点就是有回路的树形结构。图可以表示很多具体的事物,它是现实的一种抽象模型。比如地图寻址、路由寻址、状态机等。图是用来当做计算模型使用的,在某些高级场合十分适用。
- 图的定义
图的定义主要通过两种方式:1.邻接矩阵;2.邻接表。
还有一种非常复杂的定义:十字链表。
邻接矩阵的定义十分的直观,它通过二维矩阵来表示节点之间的消耗。比如a[i][j]表示从i节点到j节点的消耗,可以定义为0则没有通路。 在无向图中,通常这个矩阵是对称阵,即a[i][j] = a[j][i];在有向图中,它是反对称阵,即a[i][j] = -a[j][i]。可以看到使用邻接矩阵来存储消耗了额外的一半空间,但是查询非常的方便。
邻接表,使用邻接表来存储图,则存储一个链表数组,每个头结点就是图的节点,它指向与它有联系的节点并存储消耗。这种方式节省了空间,但是查询节点是否有联系的时候必须遍历链表,这样增加了时间的消耗。
图的种类大概会有:无向图,有向图,双向图。
Java的邻接矩阵实现,用一个类存储矩阵,在构造函数时候传入大小,新建的是n*n的矩阵,然后就是写API了,无外乎CRUD。
package Graph; import java.util.ArrayList; import java.util.List; /** * 邻接矩阵 * @author ctk * */ public class AdjacencyMatrixGraph { private int edges ; private int[][] weight; private List<String> nodes; private int vertex; public AdjacencyMatrixGraph(int vertex){ this.vertex = vertex; weight = new int[vertex][vertex]; nodes = new ArrayList<>(vertex); edges = 0; } //获得节点数 public int getNodes(){ return nodes.size(); } //获得边数 public int getEdges(){ return edges; } //插入节点 public boolean insertNode(String name){ if(nodes.size() == vertex) return false; nodes.add(name); return true; } //设置权重 public boolean setWeight(int i,int j,int weight){ if(i >= vertex || j >= vertex || i < 0 || j < 0) return false; if(this.weight[i][j] == 0) edges++; this.weight[i][j] = weight; return true; } //获得i节点 public String getNode(int i){ if(i > nodes.size()) return null; else return nodes.get(i); } //获得边权重 public int getWeight(int i,int j){ if(i >= vertex || j >= vertex || i < 0 || j < 0) return -1; else return weight[i][j]; } //删除边 public void deleteEdge(int i,int j){ if(i >= vertex || j >= vertex || i < 0 || j < 0){ System.out.println("越界"); return ; } weight[i][j] = 0; } //打印矩阵 public void printMatrix(){ for(int i=0;i<weight.length;i++) { for(int j=0;j<weight[i].length;j++){ System.out.print(weight[i][j]+" "); } System.out.println(); } } public static void main(String[] args) { AdjacencyMatrixGraph graph = new AdjacencyMatrixGraph(5); String node1 = "n1"; String node2 = "n2"; String node3 = "n3"; String node4 = "n4"; graph.insertNode(node1); graph.insertNode(node2); graph.insertNode(node3); graph.insertNode(node4); graph.setWeight(0, 1, 2); graph.setWeight(0, 2, 5); graph.setWeight(2, 3, 8); graph.setWeight(3, 0, 7); System.out.println("边数:"+graph.getEdges()); System.out.println("节点数:"+graph.getNodes()); graph.printMatrix(); } }
邻接表的实现,写一个节点类,然后初始化的时候新建这么大的数组,把每个空格放入新建的节点。
package Graph; import java.util.ArrayList; import java.util.List; /** * 邻接表实现的图 * @author ctk * */ public class ListGraph { private List<GraphNode> gNodes ; private int vertex ; private int edges ; public ListGraph(int vertex){ this.vertex = vertex ; gNodes = new ArrayList<>(vertex); for(int i=0;i<vertex;i++) { GraphNode gnode = new GraphNode(); gnode.setNodeIndex(i); gnode.setNext(null); gNodes.add(gnode); } } //添加边 public void addEdge(int i,int j,int weight){ if(i >= vertex || j >= vertex || i < 0 || j < 0) { System.out.println("输入的i和j超过范围"); return; } GraphNode gnode = gNodes.get(i); boolean isAlter = false; while(gnode.getNext() != null) { if(gnode.getNodeIndex() == j) { gnode.setData(weight); isAlter = true; break; } gnode = gnode.getNext(); } if(i == j){ gnode.setData(weight); isAlter = true; } if(!isAlter){ GraphNode edgeNode = new GraphNode(); edgeNode.setData(weight); edgeNode.setNodeIndex(j); edgeNode.setNext(null); gnode.setNext(edgeNode); } } //生成邻接矩阵 public int[][] getMartix(){ int[][] martix = new int[vertex][vertex]; GraphNode temp = null; for(int i=0;i<gNodes.size();i++){ temp = gNodes.get(i); while(temp != null){ martix[i][temp.getNodeIndex()] = temp.getData(); temp = temp.getNext(); } } return martix; } //获得某边 public int getEdge(int i,int j){ int weight = 0; if(i >= vertex || j >= vertex || i < 0 || j < 0) { System.out.println("输入的i和j超过范围"); return weight; } GraphNode temp = gNodes.get(i); while(temp != null){ if(temp.getNodeIndex() == j){ weight = temp.getData(); break; } temp = temp.getNext(); } return weight; } public int getVertex() { return vertex; } public int getEdges() { return edges; } public static void main(String[] args) { ListGraph graph = new ListGraph(5); graph.addEdge(0, 1, 2); graph.addEdge(0, 2, 3); graph.addEdge(1, 1, 4); graph.addEdge(2, 3, 6); int[][] martix = graph.getMartix(); for(int i =0;i<martix.length;i++){ for(int j=0;j<martix[i].length;j++) System.out.print(martix[i][j]+" "); System.out.println(); } System.out.println("获取边<1,1> :"+graph.getEdge(1, 1)); } } //节点类 class GraphNode{ private int nodeIndex; private int data; private GraphNode next; public int getNodeIndex() { return nodeIndex; } public void setNodeIndex(int nodeIndex) { this.nodeIndex = nodeIndex; } public int getData() { return data; } public void setData(int data) { this.data = data; } public GraphNode getNext() { return next; } public void setNext(GraphNode next) { this.next = next; } }
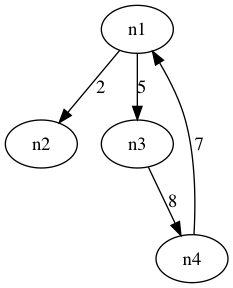
上图使用一种工具Graphviz来实现画图的,有兴趣的同学可以百度一下,有一个建模语言dot。
- 图遍历算法
对线性或者树形进行遍历,通常都十分简单,因为到null就停止了,而图是有回路的数据结构,如果使用之前的遍历策略,则很容易就死循环了。
对于图来说,遍历的策略通常是:深度优先(DFS),广度优先(BFS)。
深度优先(DFS)
对于一个节点来说,尽可能的往下走,走到尽头再去选择这个节点的另外一条路。
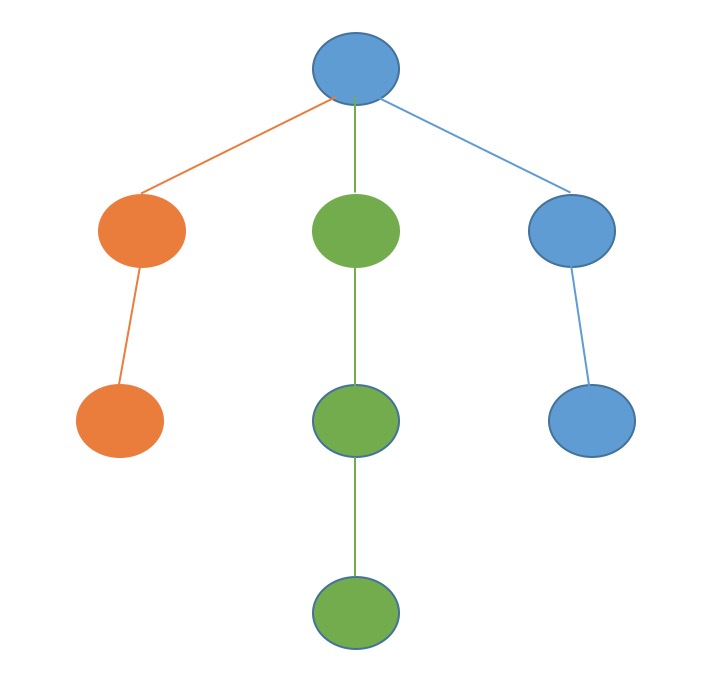
以上图来说,从根节点触发,先一个一个遍历完橙色,再遍历完绿色,最后遍历完蓝色。当然选择节点的时候有个能先绿色,也可能先蓝色,不过一旦选择一种颜色之后就会遍历到底。树形结构明白之后,图的DFS更加清楚了。
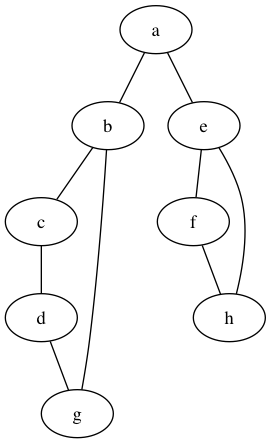
以上图为例,从a节点出发的DFS,假设装入都是按顺序的,首先遍历的是a-b-c-d-g,然后遍历e-f-h。总之顺序就是a-b-c-d-g-e-f-h。
要实现深度优先的搜索,观察这个遍历顺序,知道每次把节点拿到之后子节点优先遍历,那是一个先进后出的顺序,使用栈来存储。比如a拿到之后他的子节点b,e入栈,假设b在栈顶,则弹出遍历b后把b的子节点c,g压入栈中。如此往复,直到所有的节点都Visited。
使用C++定义一个集合专门存放节点的。
const int MAX = 100; //图节点 typedef struct { int edges[MAX][MAX]; int n; int e; int visited[MAX]; }MGraph;

这是邻接矩阵的存储方式。接着是深度优先遍历方法。并采用上述例子模型。
void DFS2(MGraph &G,int v){ stack<int> temp; cout<<"节点:"<<v<<" "; G.visited[v] = 1; temp.push(v); while(!temp.empty()){ int i,j; i=temp.top(); for(j=0;j<G.n;j++){ if(G.edges[i][j] != 0 && G.visited[j] == 0) { cout<<"节点:"<<j<<" "; G.visited[j] = 1; temp.push(j); break; } } if(j==G.n) temp.pop(); } cout<<endl; }
由于深度优先是一个栈模型,所以递归很符合它的运算模型,所以可以使用递归来计算。
void DFS1(MGraph &G,int v){ int i; cout<<"节点:"<<v<<" "; G.visited[v] = 1; for(i=0;i<G.n;i++) { if(G.edges[v][i] !=0 && G.visited[i] == 0) { DFS1(G, i); } } }
程序的运行结果是。
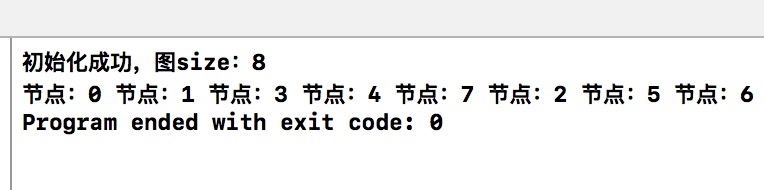
广度优先(BFS)
广度优先顾名思义,类似于树的层序遍历。把这个节点的子节点全部遍历之后,再把子节点的孩子遍历。在战争中类似于把周围的领土先占领完毕再进行扩张。
由于广度优先这个特性,使得它的实现是使用队列这种先进先出的计算模式。把父节点进入队列,然后出队列的时候把父节点的孩子节点依次加入队列尾部。
广度优先的C++代码。
void BFS(MGraph &G,int v){ queue<int> Q; cout<<"节点:"<<v<<" "; Q.push(v); while(!Q.empty()){ int i,j; i=Q.front(); Q.pop(); for(j=0;j<G.n;j++){ if(G.edges[i][j] != 0 && G.visited[j] == 0){ cout<<"节点:"<<j<<" "; G.visited[j] = 1; Q.push(j); } } } cout<<endl; }
同上例,BFS的结果是。
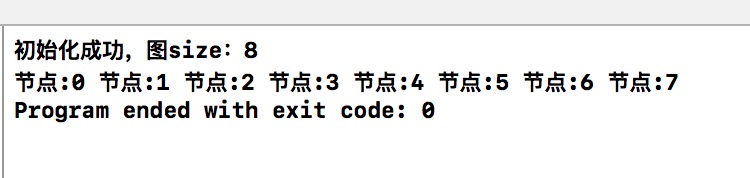
从性能上来讲,深度优先优于广度优先,因为广度优先的队列会比栈容量要大,采用哪种搜索主要看需求。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号