回溯法专题

回溯法专题

　　回溯法（Backtracking）指的是在每个状态的固化，比如f(1)是一个状态，f(2)是另一个状态。从f(1)到f(2)，状态改变，各种依赖状态的数据也改变了，那么从f(2)到f(1)的时候，又回到了f(1)的状态了。回溯常常配合深度优先执行，在往深度时候，数据产生变化，然后在递归回来的时候，又回到了之前的状态。

 

46. Permutations

 

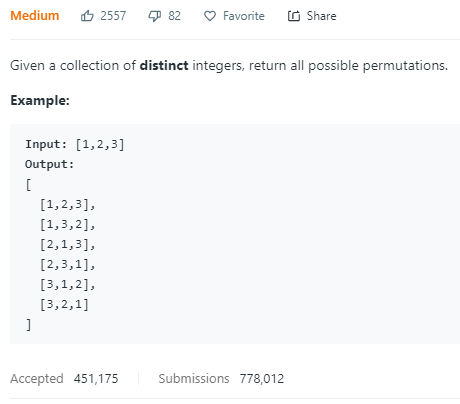
 　　拿这道全排列来讲，它按照正常顺序列出了全部的排列结果，也可以叫做字典序，主要是输入是按从小到大的话，输出就是字典序。

　　 按照递归的方式来做这道题的话，那么就是for循环的起点和变量，决定了交换哪两个数。

　　 比如输入是1,2,3，第一次交换就是 1,3,2；在递归栈出来的时候，变成1,2,3；然后再次交换是2,1,3，再是2,3,1，最后再出来的时候就会变成1,2,3。

　　 主要在这段

            swap(nums,n,j);
            sortNums(nums,n+1,len);
            swap(nums,n,j);

class Solution {
    List<List<Integer>> result = new ArrayList<List<Integer>>();
    public List<List<Integer>> permute(int[] nums) {

        if(nums ==null)
            return result;
        int len = nums.length;
        sortNums(nums, 0, len);
        return result;
    }
    public void sortNums(int[] nums, int n, int len){
        List<Integer> list = new ArrayList();
        if(len-1 ==n){
            for(int i =0; i <len; i++){
                list.add(nums[i]);

            }
            result.add(list);
            return;
        }
        for(int j =n; j <len; j++){
            swap(nums,n,j);
            sortNums(nums,n+1,len);
            swap(nums,n,j);     
        }
    }
    public void swap(int[] nums, int n, int j){
        int temp = 0;
        temp = nums[n];
        nums[n] = nums[j];
        nums[j] = temp;
    }
}

 

47. Permutations II

 

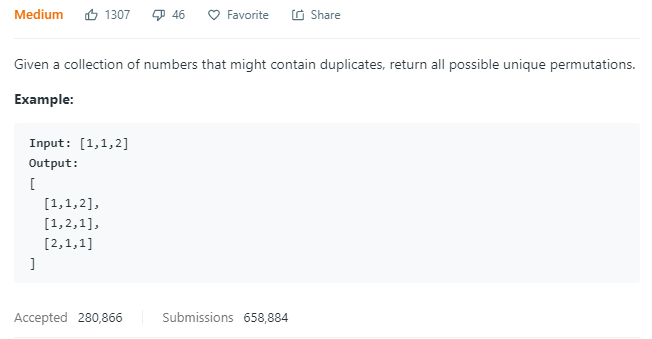
 　　在这道题中，它拥有重复元素，在排列的时候使用上一题的swap方式，那么会有两个1,1,2出来，题意是过滤掉这个重复值，可以使用set过滤。

class Solution {
    public List<List<Integer>> permuteUnique(int[] nums) {
        List<List<Integer>> result = new ArrayList<List<Integer>>();
        if(nums == null){
            return  result;
        }else if(nums.length < 2){
            List<Integer> rList = new ArrayList<Integer>();
            for(int v : nums){
                rList.add(v);
            }
            result.add(rList);
            return result;
        }
        Set<Long> filter = new HashSet<Long>();
        perm(nums,0,nums.length-1,result,filter);

        return result;

    }

    void perm(int[] nums,int k,int m,List<List<Integer>> result,Set<Long> filter){
        if(k == m){
            List<Integer> rList = new ArrayList<Integer>();
            long tag = 0;
            for(int v :nums){
                tag = tag * 10 + v;
                rList.add(v);
            }
            if(!filter.contains(tag)){
                result.add(rList);
                filter.add(tag);
            }

        }else {
            for(int i=k;i<=m;i++){
                if(i != k && nums[i] == nums[k])
                    continue;
                swap(nums,i,k);
                perm(nums,k+1,m,result,filter);
                swap(nums,i,k);
            }
        }
    }

    boolean swap(int[] nums,int i,int j){
        if(i == j)
           return false;
        int temp = nums[i];
        nums[i] = nums[j];
        nums[j] = temp;
        return true;
    }

}

 

79. Word Search

 

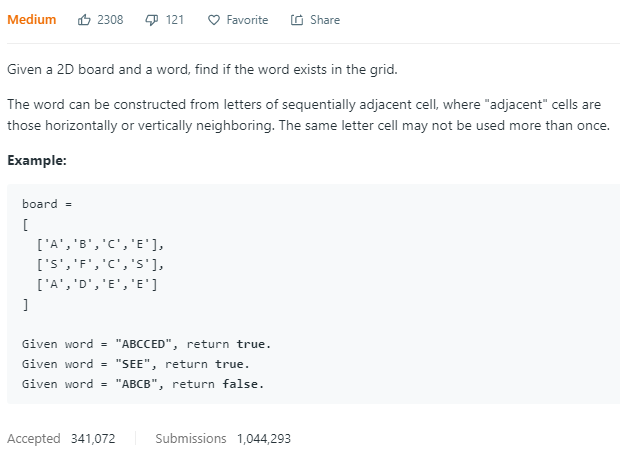
 　　这个题目乍一看懵逼，仔细看就知道了，一个迷宫，如果能吃掉你输入的序列，那么就是true，这是回溯的经典题目。

　　 关键点是朝着四个方向尝试，并且使用数组visited标记是否已经访问过，记得再出栈的时候将visited还原。

public class WordSearch {
    public void test(){
        char[][] board ={
                {'A','B','C','E'},
                {'S','F','C','S'},
                {'A','D','E','E'}
        };
        // true
        System.out.println(exist(board,"ABCCED"));
        // true
        System.out.println(exist(board,"SEE"));
        // false
        System.out.println(exist(board,"ABCB"));

        char[][] board1={
                {'A','B','C','E'},
                {'S','F','E','S'},
                {'A','D','E','E'}};
        // true
        System.out.println(exist(board1, "ABCESEEEFS"));

    }


    public boolean exist(char[][] board, String word) {
        boolean[][] visited = new boolean[board.length][board[0].length];
        for(int i=0;i<board.length;i++){
            for(int j=0;j<board[i].length;j++){
                if(dps(board,i,j,0,word,visited)){
                    return true;
                }
            }
        }
        return false;
    }
    boolean dps(char[][] board,int i,int j,int index,String word,boolean[][] visited){
        if(index >= word.length()){
            return true;
        }
        if(i<0 || i>=board.length){
            return false;
        }
        if(j<0 || j>=board[0].length){
            return false;
        }
        if(visited[i][j]){
            return false;
        }
        if(board[i][j] == word.charAt(index)){
            visited[i][j]=true;
            boolean exist = dps(board,i-1,j,index+1,word,visited) || dps(board,i+1,j,index+1,word,visited)
                    || dps(board,i,j+1,index+1,word,visited) || dps(board,i,j-1,index+1,word,visited);
            visited[i][j]=false;
            return exist;
        }else {
            return false;
        }
    }
}

 

78. Subsets

 

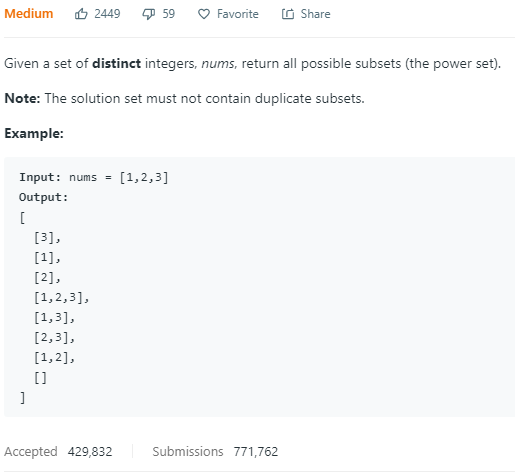
 　　集合子集分割，高中数学第一章。

class Solution {
    public List<List<Integer>> subsets(int[] nums) {
        List<List<Integer>> result = new ArrayList<>();
        if(nums == null || nums.length == 0){
            return result;
        }
        recursion(nums,0,new ArrayList<>(),result);
        return result;
    }
    void recursion(int[] nums,int i,List<Integer> each,List<List<Integer>> result){
        if(i>=nums.length){
            result.add(new ArrayList<>(each));
        }else {
            each.add(nums[i]);
            recursion(nums,i+1,each,result);
            each.remove(each.size()-1);
            recursion(nums,i+1,each,result);
        }
    }
}

90. Subsets II

 

 　　重复元素的子集分割。

class Solution {
    public List<List<Integer>> subsetsWithDup(int[] nums) {
        List<List<Integer>> result = new ArrayList<>();
        if(nums == null || nums.length == 0){
            return result;
        }
        Arrays.sort(nums);
        Set<List<Integer>> filter = new HashSet<>();
        recursion(nums,0,new ArrayList<>(),filter);
        result.addAll(filter);
        return result;
    }
    void recursion(int[] nums, int i, List<Integer> each, Set<List<Integer>> result){
        if(i >= nums.length){
            result.add(new ArrayList<>(each));
        }else {
            each.add(nums[i]);
            recursion(nums,i+1,each,result);
            each.remove(each.size()-1);

            recursion(nums,i+1,each,result);
        }
    }
}