贪心总结

贪心专题

　　贪心（Greedy）的问题我接触不多，它的基本思想很像是在递进状态的时候，采取最有利的方向。比如找零问题，有[1,2,5]面额的硬币，找16块钱，贪心的策略就是用最大的面额整除，余数用比当前小的面额继续整除，最后就得到硬币的数量，这里是5*3+1，4枚硬币。

　　与动态规划相比，动态规划类似于在f(n-1)到f(n)的过程中，保持f(n-1)是众多子结构中最优的；而贪心则是只选择当前最优的决策，这样导致可能不是全局最优的选择。

　　需要使用贪心决策的地方，需要证明在这种决策下能达到全局最优，当然这个证明我是不会，都是靠经验判断。

55. Jump Game

 

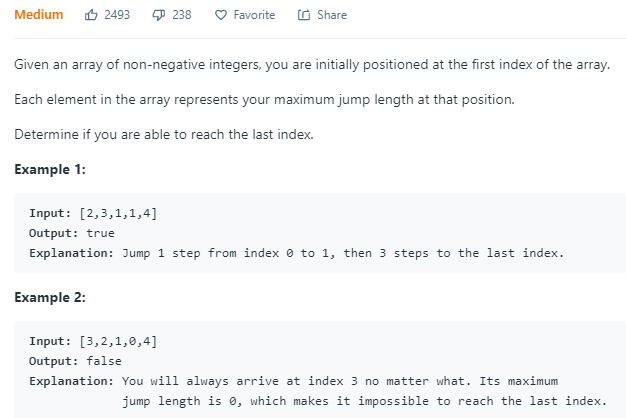
　　这个问题的意思是，从起点开始，每个位置表示你能跳的最大位置 。需要计算的是，从起点开始是否能跳到终点。

　　这里可以假设你有一个步长范围，每次你到达一个位置的时候，是否能突破你的最大步长，这样遍历到停止就能知道是否到达终点。

　　对于n，它取的是当前步长与最大步长相比，如最大者，非常典型的贪心决策。

class Solution {
    public boolean canJump(int[] nums) {
        if(nums == null || nums.length == 0){
            return true;
        }
        int reach = nums[0];
        for(int i=0;i<=reach;i++){
            if(reach<i+nums[i])
                reach = i+nums[i];
            if(reach >= nums.length-1)
                return true;
        }
        return false;
    }

}

　　

45. Jump Game II

 

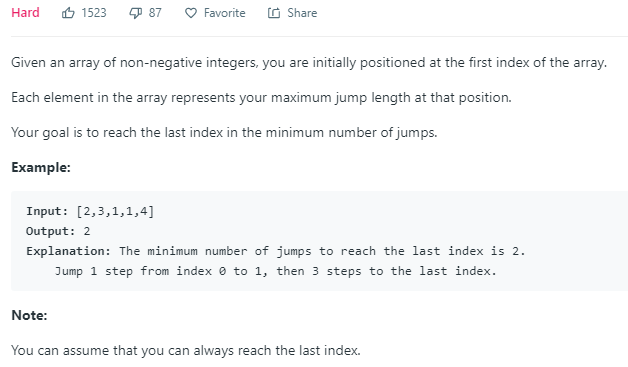
 　　这个问题是上个问题的基础上，再进了一步。就是要求算出从起点跳用最少的步骤达到终点。

　　 它的思路，就是在第一问的基础上做一个决策。我们为什么要扩大区间，扩大区间意思是一次能跳的最大步长，那每次都用最大步长去跳就是所求了。变相来说，就是区间扩大的时候，就算是一步。

class Solution {
    public int jump(int[] nums) {
        if(nums.length <= 1){
            return 0;
        }

        int reach = 0;
        int max = 0;
        int times = 0;
        for(int i=0;i<=reach;i++){
            if(i+nums[i] > max){
                max = i + nums[i];
            }
            if(i == reach){
                reach = max;
                times ++;
                if(reach >= nums.length-1)
                    break;
            }
        }
        return reach >= nums.length-1?times:0;
    }
}

 12. Integer to Roman

 

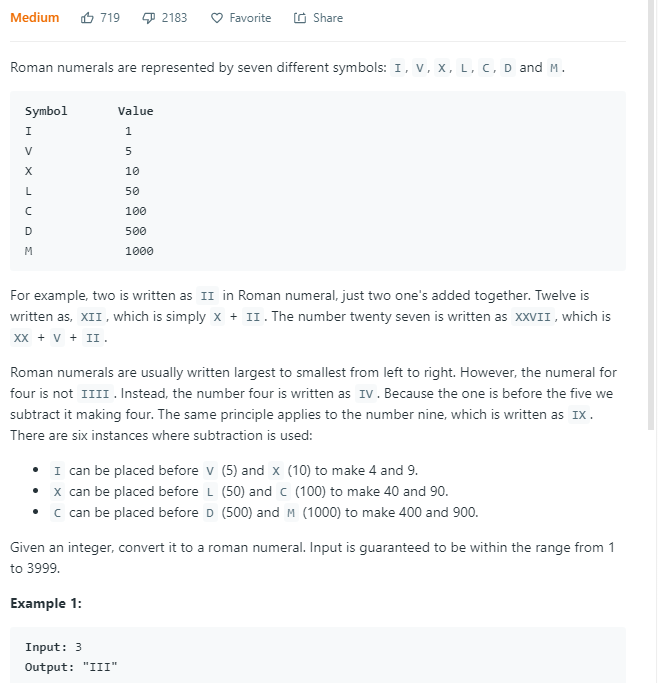
 　　将十进制数转化为罗马数字。

　　 使用贪心决策，先转化最大的单位，然后逐个降低单位。

class Solution {
    public String intToRoman(int num) {
        StringBuilder str = new StringBuilder();
        String symbol[]={"M","CM","D","CD","C","XC","L","XL","X","IX","V","IV","I"};
        int value[]=    {1000,900,500,400, 100, 90,  50, 40,  10, 9,   5,  4,   1};
        for(int i=0;num!=0;++i)
        {
            while(num>=value[i])
            {
                num-=value[i];
                str.append(symbol[i]);
            }
        }
        return str.toString();
    }
}

11. Container With Most Water

 

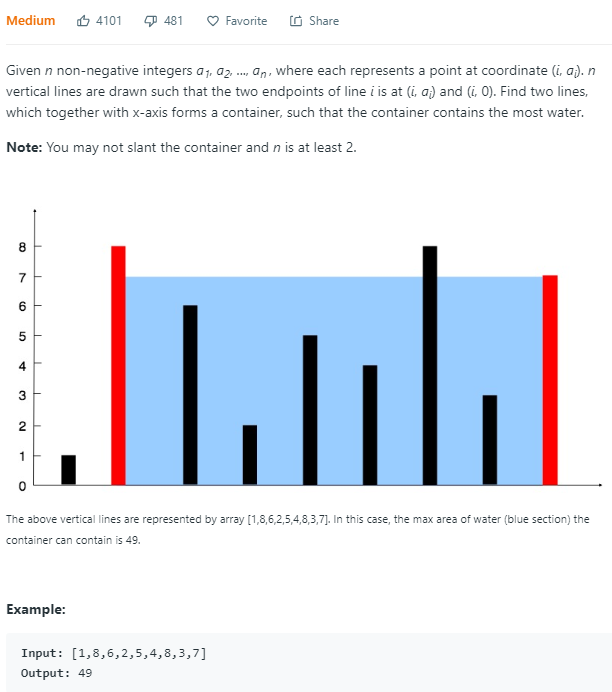
 　　小的那端往中间移动，保证大的端。

class Solution {
    public int maxArea(int[] height) {
        int maxarea = 0, l = 0, r = height.length - 1;
        while (l < r) {
            maxarea = Math.max(maxarea, Math.min(height[l], height[r]) * (r - l));
            if (height[l] < height[r])
                l++;
            else
                r--;
        }
        return maxarea;
    }
}