树形逻辑套路总结
一.决策
给定一个集合,和一个随机数字,求这个集合是否存在和为此随机数的组合。例如{1,2,3},target=2,可以找到a[1]为2;target=4,可以找到a[0]+a[2]=4;target=0,则找不到元素累加为0。
按照决策的思想,我们对元素的所有组合是一个0和1的过程。比如在第一个元素开始,我们可以选择加或者不加入等式中,这就有两个分支了:(1)a[0]+....;(2).....。

整个程序运行就如图一样,是一个树形结构。
public boolean isCount(int[] nums,int target){ return decision(nums,0,0,target); } boolean decision(int[] nums,int i,int count,int target){
if(i == nums.length){
return count == target; }else { return decision(nums,i+1,count+nums[i],target) || decision(nums,i+1,count,target); } }
由程序可见,它是深度优先的,而深度优先搜索会有很多计算浪费的情况,这个时候就要涉及到剪枝了,怎么剪枝呢,把不需要计算的情况剔除掉。
boolean decision(int[] nums,int i,int count,int target){ if(count == target){ return true; }else if(count > target){ return false; } if(i == nums.length){ return count == target; }else { return decision(nums,i+1,count+nums[i],target) || decision(nums,i+1,count,target); } }
当和等于目标随机数的时候,提前结束返回true,而在和大于目标随机数的时候,未来的计算将会是无用的,直接返回false。
假设target=1,则我们需要把大于1的全部剪掉。

接下来另一个例子,leetcode 17. Letter Combinations of a Phone Number

将2和3的字符集按顺序组合,这个题是决策思想的另一种应用。设第一个字母a的字符集为a[n],第二个字母b的字符集为b[m]。
输入ab两个字符,应该出现的结果是i:0->n,j:0->m,a[i]+b[j]。
public List<String> letterCombinations(String digits) { String[] letters = {"abc","def","ghi","jkl","mno","pqrs","tuv","wxyz"}; List<String> result = new ArrayList<String>(); createResult(digits,0,letters,"",result); return result; } void createResult(String digits,int i,String[] letters,String letter,List<String> result){ if(i == digits.length()){ if(!letter.isEmpty()) result.add(letter); return; }else { int base = 50; int index = (int)digits.charAt(i)-base; for(int j=0;j<letters[index].length();j++){ createResult(digits,i+1,letters,letter+letters[index].charAt(j),result); } } }
这题不能剪枝了,因为它要的是全部的情况。
二.递推
在数学的数列中,标志一个数列的规律的称为递推公式,比如等差数列的递推公式为:a[n]-a[n-1]=d,等比数列的递推公式为:a[n] = a[n-1]*q。而递推公式就是一次递归,特别是n为正整数,f为抽象函数的时候。

比如斐波那契数列f(n)=f(n-1)+f(n-2)这个递推公式。计算递推公式通过递归可读性强,但是性能比较差,容易爆栈。
class Solution { public int climbStairs(int n) { if(n <= 1){ return 1; }else { return climbStairs(n-1)+climbStairs(n-2); } } }
输入的n大了就会爆栈,并且时间和很长。

仔细一看这个递推公式改成循环,性能提升就不止一点点了。
class Solution { public int climbStairs(int n) { if(n <= 1){ return 1; }else { int an_2=1; int an_1 = 1; int an = 0; for(int i=2;i<=n;i++){ an = an_2 + an_1; an_2 = an_1; an_1 = an; } return an; } } }
这道题就是非常受到面试欢迎的题目了,它虽然是easy等级的,但是它为一维动归提供了一些思想基础。
这道题可以自顶向下分析,比如我走n阶梯,方法有f(n)种,那f(n)是由什么组成的?因为一次可以走一步或者两步,则f(n)应该可以倒着走一步或者两步。倒走一步为f(n-1)种方法,倒走两步为f(n-2)种方法,所以f(n)=f(n-1)+f(n-2),为本题的递推公式。它的初始值很容易就能计算出来,f(0)=0,f(1)=1,f(2)=2,f(3)=f(1)+f(2)=3...
再看一个递推的应用。
这是一道一维动归的简单题,要求我们不能抢两家连续的,在这种约束下抢最大利益。
设f(n)为n家抢劫的最大利益,f(n)=max{f(n-1),f(n-2)+A[n]}。很显然如果你要加上A[n]你必须隔开相邻。
递推的初始值为f(1)=A[1],f(2)=max{A[1],A[2]}。
class Solution { public int rob(int[] nums) { if(nums == null || nums.length == 0){ return 0; }else if(nums.length == 1){ return nums[0]; }else { int a1 = nums[0]; int a2 = Math.max(nums[1],nums[0]); int f = Math.max(a1,a2); for(int i=2;i<nums.length;i++){ f = Math.max(a1+nums[i],a2); a1 = a2; a2 = f; } return f; } } }
三.二分
二分查找,实际上是一个二叉查找树。二分查找的先决条件,就是这个数组是有序数组。它拥有如下的算法骨架。
int left,right; while(left < right){ int medium = (right-left)/2 + left; if(target > a[medium]){ left = medium + 1; }else if(target < a[medium]){ right = medium - 1; }else{ break; } }

有序,但是是重复元素怎么办?二分完了然后中心扩展不就完了。
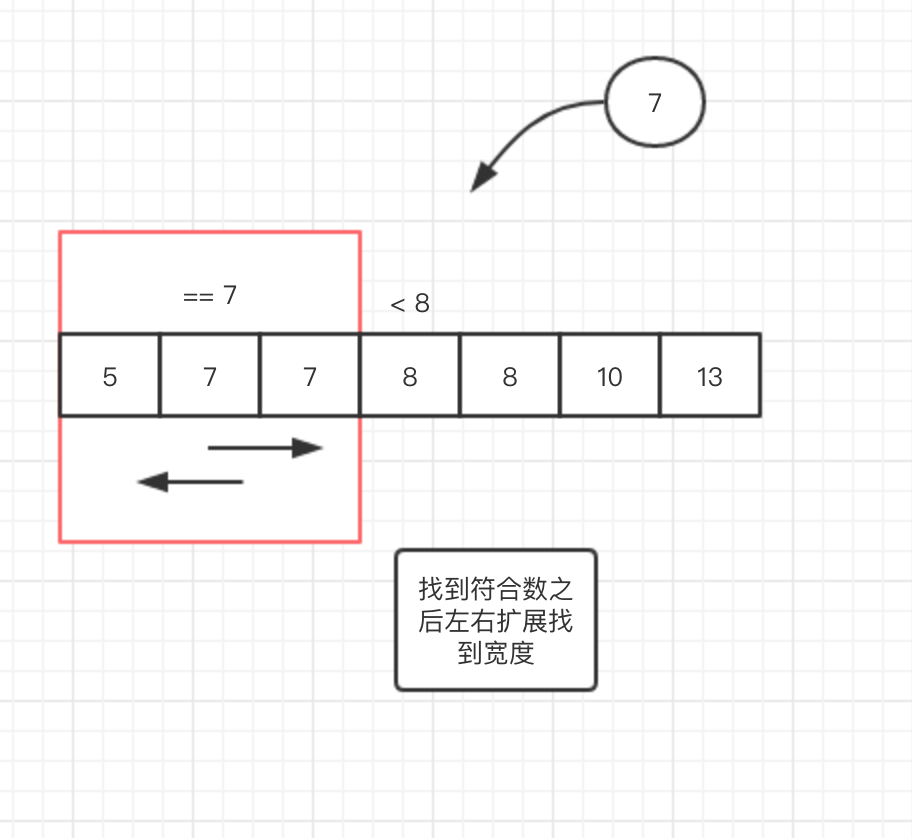
class Solution { public int[] searchRange(int[] nums, int target) { int left = 0,right = nums.length -1; int leftIndex = -1,rightIndex = -1; if(nums.length == 0){ return new int[]{leftIndex,rightIndex}; }else if(nums.length == 1){ if(nums[0] == target){ leftIndex = 0; rightIndex = 0; } return new int[]{leftIndex,rightIndex}; } while(left <= right){ int mid = left + (right - left)/2; if(nums[mid] > target){ right = mid - 1; }else if(nums[mid] < target){ left = mid + 1; }else { int i = mid; int j = mid; while(true){ if(i-1 >= 0 && nums[i-1] == target){ i--; }else { break; } } while(true){ if(j+1 < nums.length && target == nums[j+1]){ j++; }else { break; } } leftIndex = i; rightIndex = j; break; } } return new int[]{leftIndex,rightIndex}; } }
下面这个题让我又爱又恨。

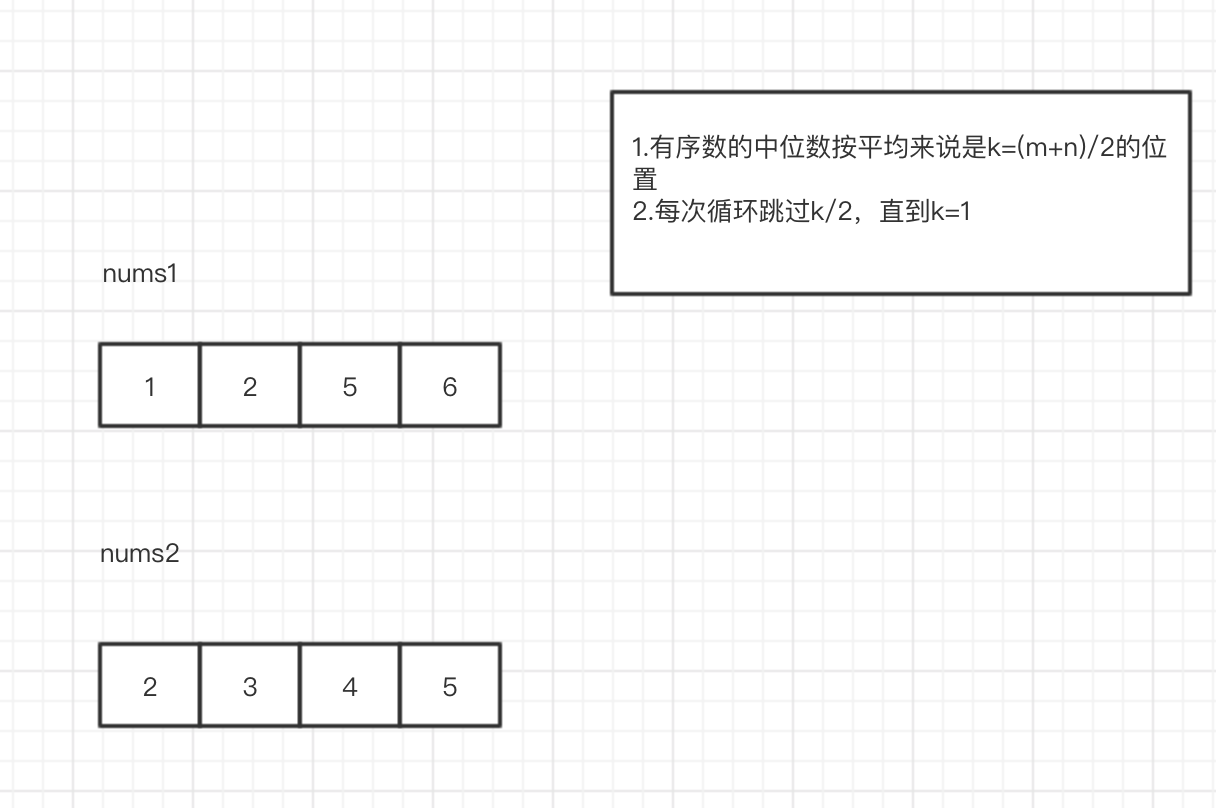
public double findMedian(int[] nums1,int[] nums2){ int n = nums1.length; int m = nums2.length; int total = n+m; if(total %2 != 0){ return divide(nums1,0,n-1,nums2,0,m-1,(n+m)/2+1); }else { return 0.5*(divide(nums1,0,n-1,nums2,0,m-1,(n+m)/2) + divide(nums1,0,n-1,nums2,0,m-1,(n+m)/2 + 1)); } } double divide(int[] nums1,int start1,int end1,int[] nums2,int start2,int end2,int k){ int a = end1 - start1 + 1; int b = end2 - start2 + 1; // 让nums1始终是最短的数组 if(a > b){ return divide(nums2, start2, end2, nums1, start1, end1, k); } // 如果数组nums1已经没有"余额",则直接到nums2取满k if(a == 0){ return nums2[start2 + k-1]; } // 当k减少到1时候,从start1和start2选最小的一个 if(k == 1){ return Math.min(nums1[start1],nums2[start2]); } // 将k分为k/2 以及 k - k/2 两部分 // 如果 a数组即将走到尽头并且不足k/2,则使用a数组剩余部分 int addA = Math.min(k/2,a); int addB = k - addA; // 预计跳转的地方将舍弃小的部分 if(nums1[start1+addA - 1] > nums2[start2+addB - 1]){ return divide(nums1,start1,end1,nums2,start2+addB,end2,k-addB); }else { return divide(nums1,start1+addA,end1,nums2,start2,end2,k-addA); } }
四.回溯
回溯,指的是我从a->b->c状态的时候,从c能回到b状态,然后从b能回到a状态。
经典案例,全排列的递归算法。算法思路是,将a[i]与k:i->n中随意元素进行位置更换,再返回的时候再换回来,这个换回来的过程就是回溯。
void perm(int[] nums,int k,int m,List<List<Integer>> result){ if(k == m){ List<Integer> rList = new ArrayList<Integer>(); for(int v :nums){ rList.add(v); } result.add(rList); }else { for(int i=k;i<=m;i++){ swap(nums,i,k); perm(nums,k+1,m,result); swap(nums,i,k); } } } void swap(int[] nums,int i,int j){ if(i == j) return ; int temp = nums[i]; nums[i] = nums[j]; nums[j] = temp; }
在for循环里面,先将i与k位置调换,然后进入递归,再递归出来的时候又将i与k调换回来,这是一种恢复状态的行为,成为回溯。

这道题和决策的第一个例子很像,但是它是允许重复元素累加的,这个思维就像返回过来一样。我们最开始的例子是把它加上去,这回我们要把它减掉。
public class CombinationSum { public List<List<Integer>> combinationSum(int[] candidates, int target) { List<List<Integer>> result = new ArrayList<>(); if(candidates == null || candidates.length < 1){ return result; } count(candidates,0,target,result,new ArrayList<>()); return result; } void count(int[] nums,int i,int target,List<List<Integer>> result ,List<Integer> eachList){ if(target < 0){ return ; }else if(target == 0){ result.add(new ArrayList<>(eachList)); return ; }else { for(int j=i;j<nums.length;j++){ eachList.add(nums[j]); count(nums,j,target-nums[j],result,eachList); eachList.remove(eachList.size()-1); } } } }
同样我们使用了回溯的方法,在加入这个元素之后进入递归,递归出来之后去掉这个元素,很遗憾不是很快。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号