蓝桥杯——算法分析

蓝桥杯比赛：对算法题进行一些整理，以C语言为主。

题目：

1.杨辉三角形

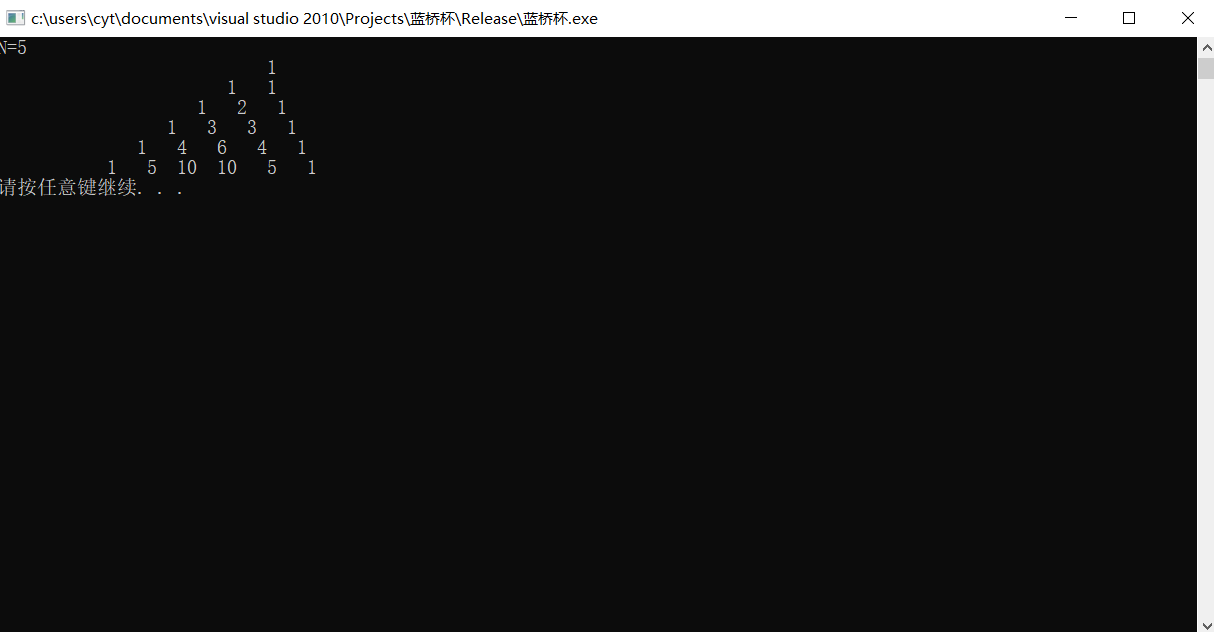
在屏幕上显示杨辉三角形
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
......................................
问题分析与算法设计
杨辉三角形中的数，正是(x+y)的N次方幂展开式各项的系数。本题作为程序设计中具有代表性的题目，求解的方法很多，这里仅给出一种。
从杨辉三角形的特点出发，可以总结出：
1)第N行有N+1个值(设起始行为第0行)
2)对于第N行的第J个值：(N>=2)
当J=1或J=N+1时：其值为1
J!=1且J!=N+1时：其值为第N-1行的第J-1个值与第N-1行第J个值之和
将这些特点提炼成数学公式可表示为：
1 x=1或x=N+1
c(x,y)= c(x-1,y-1)+c(x-1,y) 其它
本程序应是根据以上递归的数学表达式编制的。

源代码：

#include<stdio.h>
#include<stdlib.h>

int c(int x,int y)     /*求杨辉三角形中第x行第y列的值*/
{
    int z;
    if((y==1)||(y==x+1))  return 1;  /*若为x行的第1或第x+1列，则输出1*/
    z=c(x-1,y-1)+c(x-1,y);          /*否则，其值为前一行中第y-1列与第y列值之和*/
    return z;
}
void main()
{
    int i,j,n=13;
    printf("N=");
    while(n>12)
        scanf("%d",&n);     /*控制输入正确的值以保证屏幕显示的图形正确*/
    for(i=0;i<=n;i++)       /*控制输出N行*/
    {
        for(j-0;j<24-2*i;j++) printf(" ");  /*控制输出第i行前面的空格*/
        for(j=1;j<i+2;j++) printf("%4d",c(i,j));    /*输出第i行的第j个值*/
        printf("\n");
    }
    system("pause");
}

运行结果：

 

 2.歌德巴赫猜想
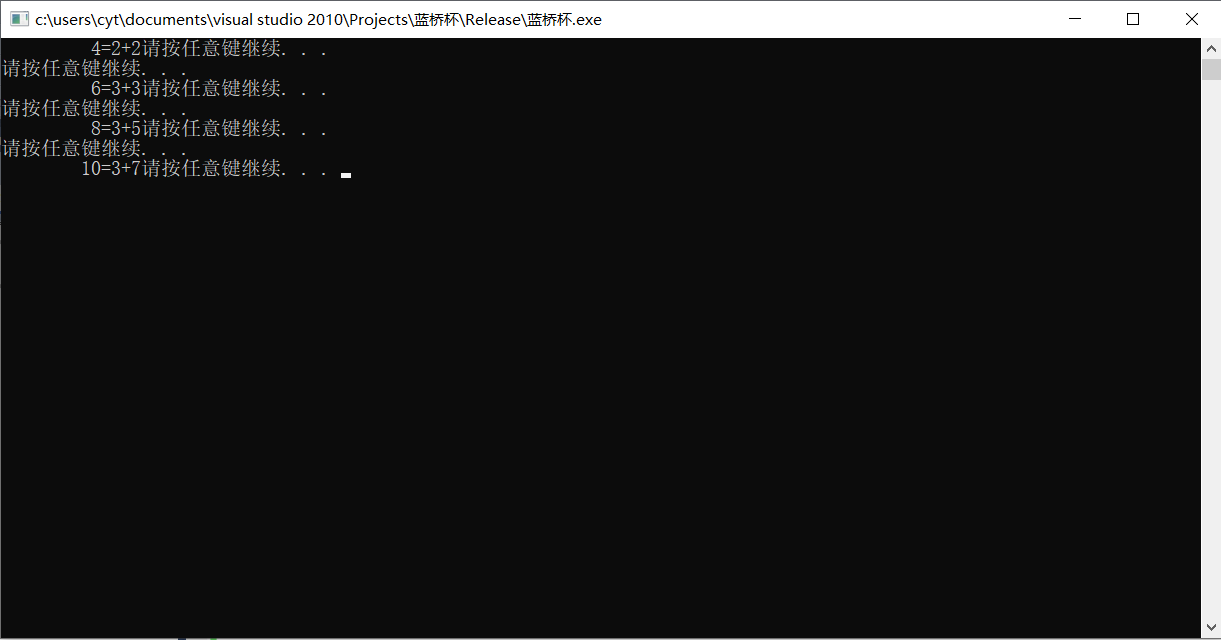
     验证：2000以内的正偶数都能够分解为两个素数之和(即验证歌德巴赫猜想对2000以内的正偶数成立)。
问题分析与算法设计：
       为了验证歌德巴赫猜想对2000以内的正偶数都是成立的，要将整数分解为两部分，然后判断出分解出的两个整数是否均为素数。若是，则满足题意；否则重新进行分解和判断。
    程序中对判断是否为素数的算法进行了改进，对整数判断“用从2开始到该整数的一半”改为“2开始到该整数的平方根”。原因何在请自行分析。

源代码：

#include<stdio.h>
#include<stdlib.h>
#include<math.h>
int flag(int n);
void main()
{
    int i,n;
    for(i=4;i<=2000;i+=2)/*范围，且保证为偶数时执行循环体*/
    {
        for(n=2;n<i;n++)         /*将偶数i分解为两个整数*/
            if(flag(n))         /*分别判断两个整数是否均为素数*/
            {
                if(flag(i-n))
                {
                    printf("%10d=%d+%d",i,n,i-n);   /*若均是素数则输出*/
                    break;
                }
            
            }
                
            if(n==i) 
            {
                printf("error %d",i);
                break;
            }
    }
} 
int flag(int i)           /*判断是否为素数*/
{
    int j;
    if(i<=1)return 0;
    if(i==2)return 1;
    if(!(i%2))return 0;     /*if no,return 0*/
    for(j=3;j<=(int)(sqrt((double)i)+1);j+=2)/*求平方根*/
    {
        if(!(i%j))/*判断是否为素数*/
        {
            return 0;
        }
            
    }   
    system("pause");
    return 1;              /*if yes,return 1*/

}

运行结果：

 

 

3.马克思手稿中的数学题
    马克思手稿中有一道趣味数学问题：有30个人，其中有男人、女人和小孩，在一家饭馆吃饭花了50先令；每个男人花3先令，每个女人花2先令，每个小孩花1先令；问男人、女人和小孩各有几人？

题目分析与算法设计：
    设x,y,z分别代表男人、女人和小孩。按题目的要求，可得到下面的方程：
                   x+y+z=30            (1)
                   3x+2y+z=50          (2)
    用方程程序求此不定方程的非负整数解，可先通过(2)-(1)式得：
                   2x+y=20             (3)
由(3)式可知，x变化范围是0~10
源代码：

#include<stdio.h>
#include<stdlib.h>
void main()
{
    int x,y,z,count=0;
    printf("            Men      Women     Children\n");
    printf("==========================================\n");
    for(x=0;x<=10;x++)
    {
        y=20-2*x;                     /*x定值据(3)式求y*/
        z=30-x-y;                     /*由(1)式求z*/
        if(3*x+2*y+z==50)             /*当前得到的一组解是否满足式(2)*/
            printf(" %2d:         %d         %d         %d\n",++count,x,y,z);
    }
    system("pause");
}

运行结果：

 

 

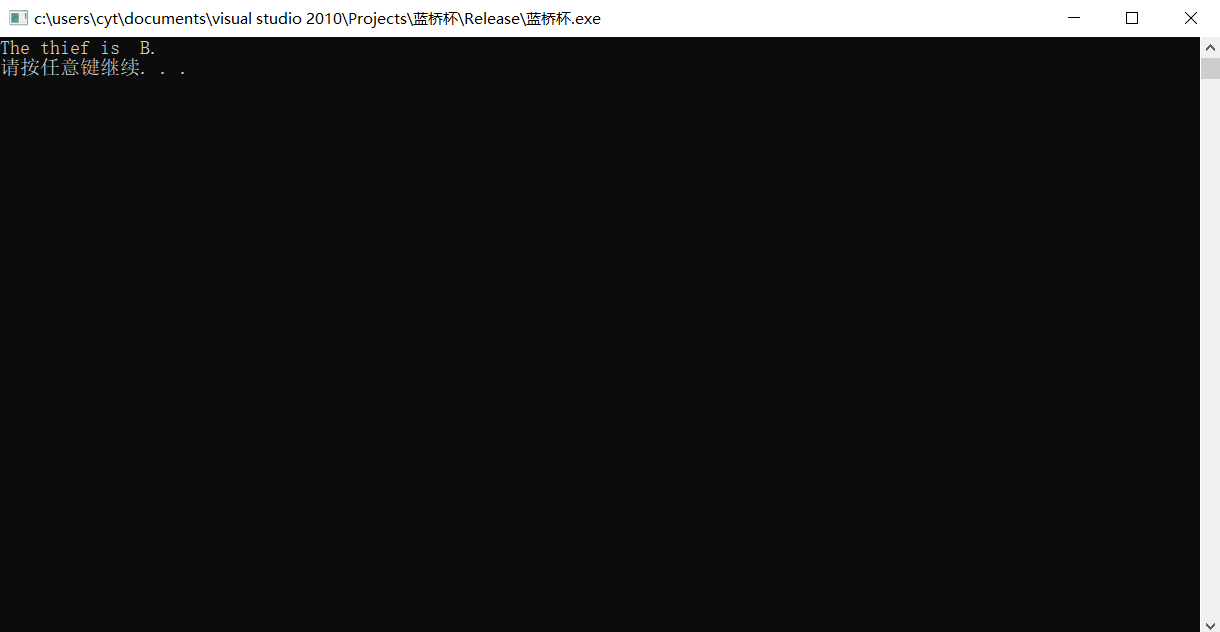
4.谁是窃贼
    公安人员审问四名窃贼嫌疑犯。已知，这四人当中仅有一名是窃贼，还知道这四人中每人要么是诚实的，要么总是说谎的。在回答公安人员的问题中：
        甲说：“乙没有偷，是丁偷的。”
        乙说：“我没有偷，是丙便的。”
        丙说：“甲没有偷，是乙偷的。”
        丁说：“我没有偷。”
    请根据这四人的答话判断谁是盗窃者。

问题分析与算法设计：
    假设A、B、C、D分别代表四个人，变量的值为1代表该人是窃贱。
    由题目已知：四人中仅有一名是窃贱，且这四个人中的每个人要么说真话，要么说假话，而由于甲、乙、丙三人都说了两句话：“X没偷，X偷了”，故不论该人是否说谎，他提到的两人中必有一人是小偷。故在列条件表达式时，可以不关心谁说谎，谁说实话。这样，可以列出下列条件表达式：
        甲说：”乙没有偷，是丁偷的。”        B+D=1
        乙说：“我没有偷，是丙偷有。”        B+C=1
        丙说：“甲没有偷，是乙偷的。”        A+B=1
        丁说：“我没有偷。”                  A+B+C+D=1
    其中丁只说了一句话，无法判定其真假，表达式反映了四人中仅有一名是窃贱的条件。
源代码：

#include<stdio.h>
#include<stdlib.h>
void main()
{
    int i,j,a[4];
    for(i=0;i<4;i++)            /*假定只有第i个人为窃贱*/
    {
        for(j=0;j<4;j++)        /*将第i个人设置为1表示窃贱，其余为0*/
            if(j==i)a[j]=1;
            else a[j]=0;
        if(a[3]+a[1]==1&&a[1]+a[2]==1&&a[0]+a[1]==1)   /*判断条件是否成立*/
        {
            printf("The thief is  ");              /*成立*/
            for(j=0;j<=3;j++)                   /*输出计算结果*/
                if(a[j])printf("%c.",j+'A');
            printf("\n");
        }
    }
    system("pause");
}

运行结果：

 

 

5.迷语博士的难题(1)
    诚实族和说谎族是来自两个荒岛的不同民族，诚实族的人永远说真话，而说谎族的人永远说假话。迷语博士是个聪明的人，他要来判断所遇到的人是来自哪个民族的。
    迷语博士遇到三个人，知道他们可能是来自诚实族或说谎族的。为了调查这三个人是什么族的，博士分别问了他们的问题，这是他们的对话：
    问第一个人：“你们是什么族？”，答：“我们之中有两个来自诚实族。”第二个人说：“不要胡说，我们三个人中只有一个是诚实族的。”第三个人听了第二个人的话后说：“对，就是只有一个诚实族的。”
    请根据他的回答判断他们分别是哪个族的。

问题分析与算法设计：
    假设这三个人分别为A、B、C，若说谎其值为0，若诚实，其值为1。根据题目中三个人的话可分别列出：
        第一个人： a&&a+b+c==2||!a&&a+b+c!=2
        第二个人： b&&a+b+c==1||!b&&a+b+c!=1
        第三个人： c&&a+b+c==1||!c&&a+b+c!=1
    利用穷举法，可以很容易地推出结果。
源代码：

#include<stdio.h>
#include<stdlib.h>
void main()
{
    int a,b,c;
    for(a=0;a<=1;a++)       /*穷举每个人是说谎还是诚实的全部情况*/
        for(b=0;b<=1;b++)    /*说谎：0   诚实：1*/
            for(c=0;c<=1;c++)
                if((a&&a+b+c==2||!a&&a+b+c!=2)    /*判断是否满足题意*/
                    &&(b&&a+b+c==1||!b&&a+b+c!=1)
                    &&(c&&a+b+c==1||!c&&a+b+c!=1))
                {
                    printf("A is a %s.\n",a?"honest":"lier");    /*输出判断结果*/
                    printf("B is a %s.\n",b?"honest":"lier");
                    printf("C is a %s.\n",c?"honest":"lier");
                }
    system("pause");
}

运行结果：

 

 

6.小结

数学题的逻辑 ！！！