fp32的表示精度范围计算

在 IEEE 754 标准中，浮点数表示的指数的底（基数）是 2。这意味着浮点数表示遵循二进制科学记数法，即数值表示为尾数（Significand 或 Mantissa）乘以 2 的指数次方。

浮点数表示

浮点数的表示形式通常为：

 

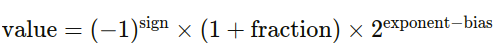
其中：

• sign：符号位，0 表示正数，1 表示负数。
• fraction：尾数位，也称为小数部分，表示为小数点右边的二进制数。
• exponent：指数位，表示 2 的幂次。
• bias：指数的偏移量，用于将指数值偏移到非负范围。

示例

假设我们有一个单精度浮点数的二进制表示：

1 10000010 10100000000000000000000

• 符号位（Sign Bit）：1（表示负数）
• 指数位（Exponent）：10000010（十进制 130）
• 尾数位（Fraction）：10100000000000000000000

计算实际值的步骤如下：

1. 计算指数：
   指数的偏移量（bias）对于单精度浮点数是 127，因此实际指数值为：

   [ E = 130 - 127 = 3 ]

2. 计算尾数：
   尾数位的二进制表示为 10100000000000000000000，在归一化表示中，尾数实际上是 1.101。归一化表示隐含了一个前导的 1，即：

   [ 1 + 0.101 = 1 + 0.625 = 1.625 ]

3. 组合成实际值：
   使用基数 2 的指数：

   value = (-1)^1 ×1.625 × 2^3 = -1.625 ×8 = -13.0 

因此，这个单精度浮点数的实际值为 -13.0。

总结

在 IEEE 754 标准中，浮点数表示的指数的底是 2，这意味着数值表示为尾数乘以 2 的某次幂。这种表示方法使得浮点数能够表示非常大和非常小的数值，同时保持相对的精度。