warm-up原理和训练技巧

原理

训练神经网络的一个重要 trick 是 warm up，它被广泛应用在各种模型的训练中。它的命名大概是类比了我们参加体育锻炼前的热身运动。warm up 通过操作训练初始阶段的 learning rate，可以使模型参数更快地收敛，并达到更高的精度。

众所周知，learning rate 如果设置的过大，有可能会导致梯度爆炸，同时也有可能会导致难以收敛到更好的 local minima；反之，如果 learning rate 过小，会导致网络训练得太慢。

在训练初期，由于网络参数是随机初始化的， loss 很大，导致 gradient 很大，此时我们希望 learning rate 小一点，防止梯度爆炸；而在训练中期，我们希望 learning rate 大一点，加速网络训练，在训练末期我们希望网络收敛到 local minima，此时 learning rate 也应该小一点。warm up 的一套流程正好迎合了这种需求。

训练初始，warm up 把学习率设置得很小，随着训练的进行，学习率逐渐上升，最终达到正常训练的学习率。这个阶段就是 warm up 的核心阶段。接着，随着训练的进行，我们希望逐渐减小学习率，（learning rate decay），训练完成时，learning rate 降为 0 。

公式

warm up 有几个重要的参数：

• ：warm up 阶段训练多少步
• ：warm up 开始时的 learning rate
• ：正式训练初始 learning rate

事实上，任何一种满足第一部分设计需求的 learning rate 更新策略都可以叫 warm up，这里只实现一种。

其中 为训练步数，。我们可以看到，当 时，初始学习率为 ；随着 的增加，学习率逐渐上升，当 时，学习率为 ，即正式训练的初始学习率。

warm up 阶段结束后，下一步是随着训练的进行，让学习率逐渐降低到 0。这里需要用到两个新的参数：

• ：总共训练的步数
• ：power，控制学习率降低的速率

 

从 (2) 可以看到，当 时， 前面的参数为 1，学习率就是 ；当 时， 前面的参数为 0，学习率为 0 。再观察 ，当 时，学习率线性降低到 0；当 时，括号里面的底数始终是大于 0 小于 1 的，因此它的 次方应该比它本身要大，因此 会让学习率比同时期线性 decay 得到的学习率更大一点；当 时，学习率比同时期线性 decay 的学习率要小。由于学习率最终都是降到了 0，显然应该设置 ，让正式训练初期学习率降得慢一点，而正式训练末期，学习率迅速降低到 0，而不是 导致正式训练初期学习率就降得很快，而正式训练末期学习率降得很慢，拖慢训练进程。

代码

参数：

• warmup_steps：，warm up 阶段训练多少步
• warmup_start_lr：，warm up 开始时的 learning rate
• lr0： ，正式训练初始 learning rate
• max_iter： ，总共训练的步数
• power：，控制学习率降低的速率

# 设置参数，一般应该写在类里，这里为了方便演示，将其提取出来。
warmup_start_lr = 1e-5
warmup_steps = 1000
max_iter = 80000
lr0 = 1e-2
power = 0.9

warmup_factor = (lr0/warmup_start_lr)**(1/warmup_steps)

def get_lr(t):
    if t <= warmup_steps:
        lr = warmup_start_lr*(warmup_factor**t)
    else:
        factor = (1-(t-warmup_steps)/(max_iter-warmup_steps))**p
        lr = lr0*factor

    return lr

下面把不同 step 对应的 learning rate 画出来：

import matplotlib.pyplot as plt
import numpy as np

steps = np.arange(max_iter)
lrs = list(map(get_lr, steps))
plt.plot(steps, lrs)
plt.show()

 

 

学习率变化图

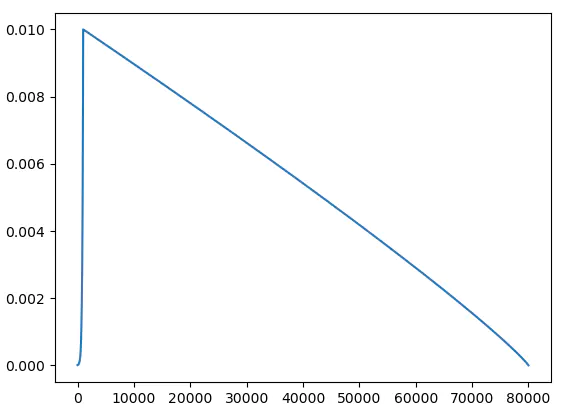
可以发现，前 1000 步 warm up 阶段，学习率由 1e-5 迅速上升到正式训练的初始学习率 1e-2，接着，随着迭代步数的增加，学习率缓慢下降，最终降为0。学习率的变化率（斜率）也也很有意思，warm up 初始阶段，斜率很低，学习率增长缓慢，代表需要维持一段时间的低学习率，以让模型更好地热身。快接近 warmup 尾声时，斜率很高，代表学习率增长得很快，以达到正式训练的初始学习率。decay 的初始阶段，学习率下降得较慢，表示需要维持一段时间的高学习率，以加快模型收敛，训练快结束时，学习率迅速下降，以便模型收敛到更好的 local minima。

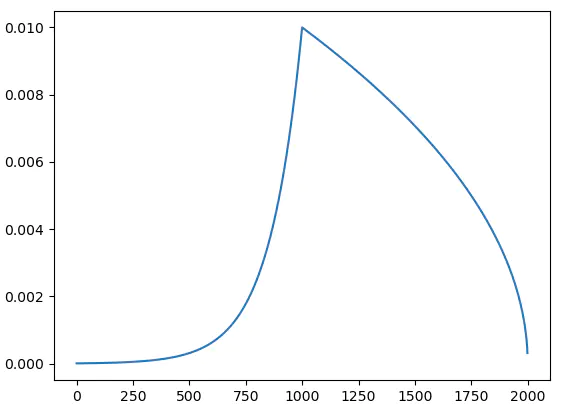
为了更好地展示上面描述的过程，这里调整一下参数（并非实际训练，实际训练时可参考上面的各种参数配置比例）。

 

 

power=0.5, max_iter=2000, 其余不变