3D空间点到直线的距离

最近公司进行了技能考试，其中有个编程题中有一步需要计算三维空间中点到直线的距离，并给出坐标

这个知识点本来觉得不难，却想不起来怎么作。网上搜索都是2D空间的做法。最后从Youtube找到一个讲解视频，这里用文字转述下。

举例：

其中 P(-6,1,21)

Line:

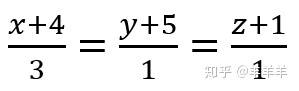
针对例子视频一共介绍了3个方法，从繁琐到简单排列：

方法 1

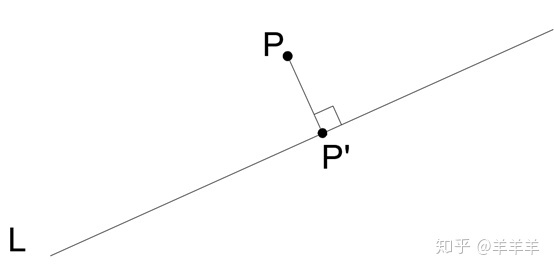
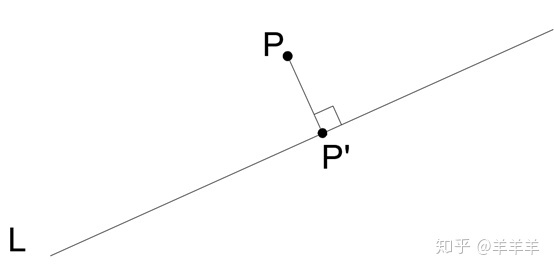
3D点到直线的距离即为PP'，P已知，如果能找到P'，问题就解决了。方法1 先计算一个以L为法线的平面，并且P 在这个平面上。这个平面和L的交点即为P'。

 

Step 1：

首先计算平面：

 

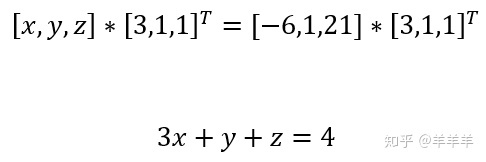
Step 2:

直线上一点可以表达为t的函数：((3t-4), (t-5), (t-1))

将点带入平面函数：

 

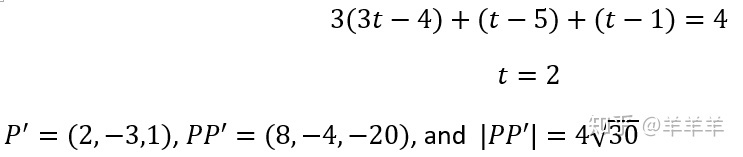
方法2

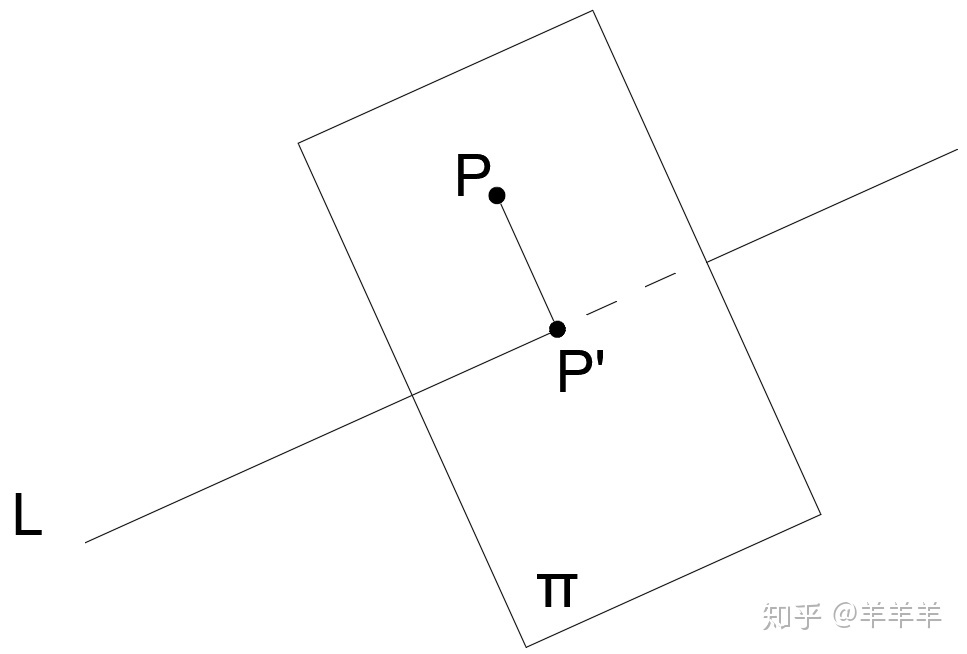
同样是寻找P'的位置，方法2考虑使用利用距离PP'垂直于直线的原理。

 

点P'位置((3t-4), (t-5), (t-1))，那么PP'为((3t+2), (t-6), (t-22)).

PP'垂直于直线L：

3*(3t+2)+(t-6)+ (t-22)=0

t=2

剩下的部分和方法1 相同。

 

方法3

这里将使用叉乘的理论，直接获得|PP'|的长度。

两个向量的叉乘结果是一个垂直于这两个向量的向量，最后这个向量的长度等于以最初两个向量作为边的平行四边形的面积。

 

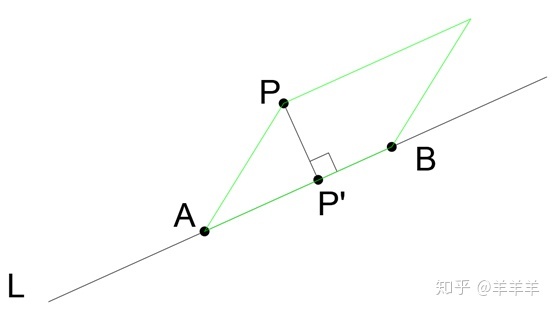
点A和点B是直线上任意两点。为了计算方便：

A(-4,-5,-1)

AB(3,1,1) and AP(-2,6,22)

平行四面形的面积：

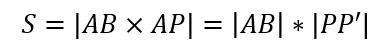
叉乘有两种计算方式：

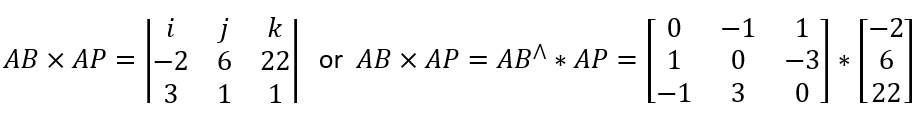
讲叉乘结果带回原等式:

 

视频地址：

https://www.youtube.com/watch?v=9wznbg_aKOo​www.youtube.com/watch?v=9wznbg_aKOo