机器学习中的泰勒级数理解（二）

【阅读内容】通过构造知识联想链条和直观例子回答什么是泰勒级数，为什么需要泰勒级数，泰勒级数干了什么，如何记忆这个公式
【原文链接】
 https://charlesliuyx.github.io

1

几何角度

 

 

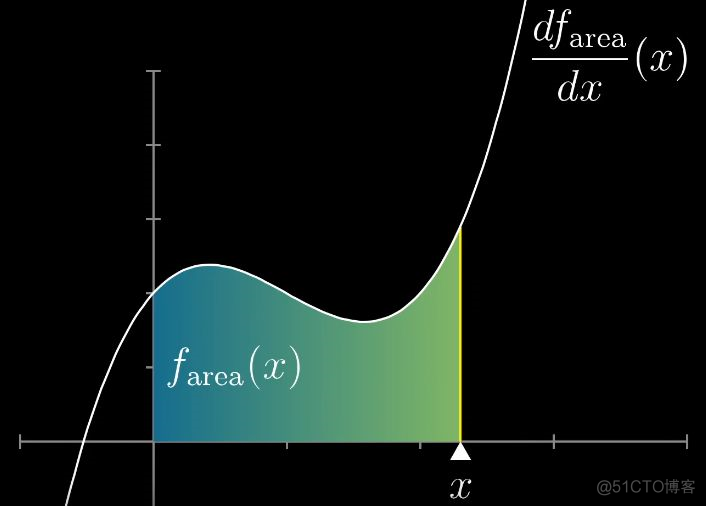
定义一个这样的场景是为了计算这样一件事（如下图所示）：假设我们知道了f(a)点的面积，往右扩展很小的距离dx要算出新部分的面积（左边绿色已知 + 黄色矩形 + 红色三角形），公式会是什么样的呢？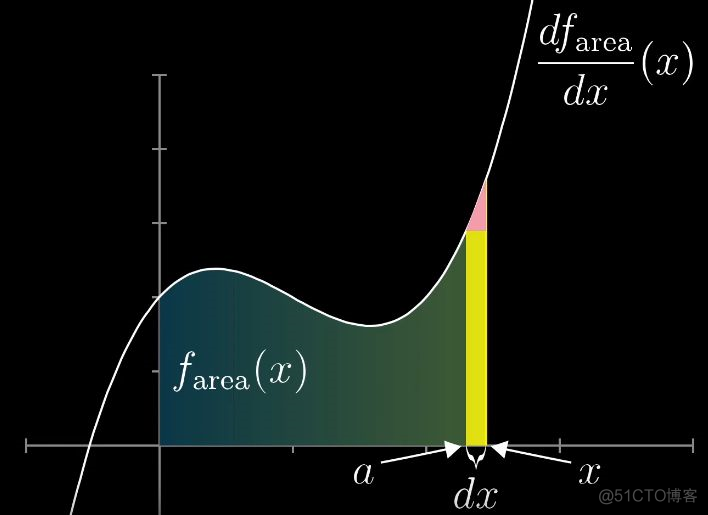

 

 

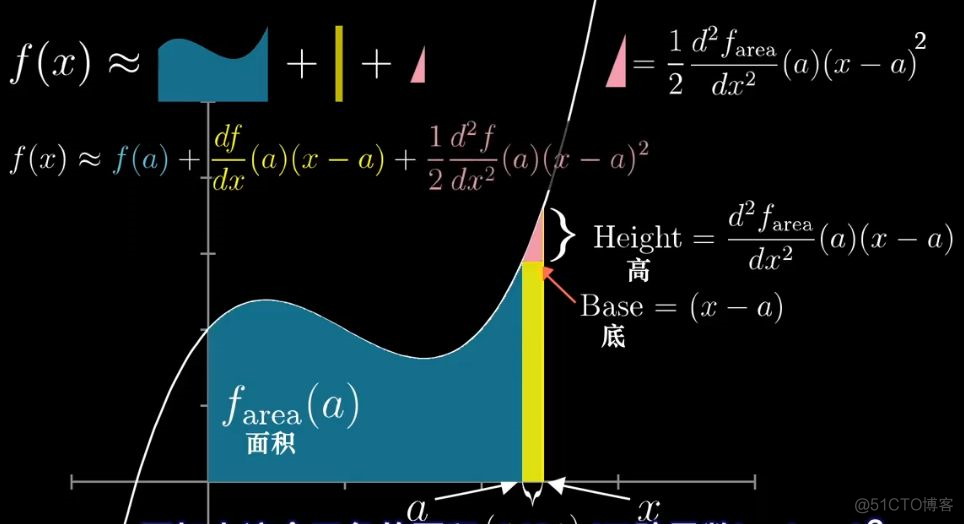
这个公式为啥这么眼熟呢？其实明显就是泰勒展开式的前3项，如果你还要打破沙锅问到底，第4项呢？你可以放大红色三角形，把函数曲线和面积之间的空白部分再次用多个更小的三角形填补，在积分工具的帮助下，可以得到三次项。

从几何角度来看，再一次验证了，泰勒公式是近似的 x=a附近的函数值这一直观理解

2

余项

我们知道，对泰勒公式来说，并没有办法完全逼近待求函数，所以无论如何到最后都会留一点东西，这剩下的东西不好表达，就全都丢到余项中。
可以暂时如此理解，不在此迷惑，如果是专业学生，需要深究，建议参看专业教材深入理解其中玄妙

3

泰勒级数

完成对【泰勒公式】的理解后，需要对【级数 Series】这个概念进行一个推广，什么是【级数】呢？
在数学中，【级数】就是无限多项的和
在把泰勒展开式，扩展到无限项之后，就会出现【收敛 Converge】和【发散 diverge】的概念

收敛

收敛，即在泰勒展开式被推广到无限项之后，整体式子的值会越来越趋近于一个定值，比如下图的1/2和e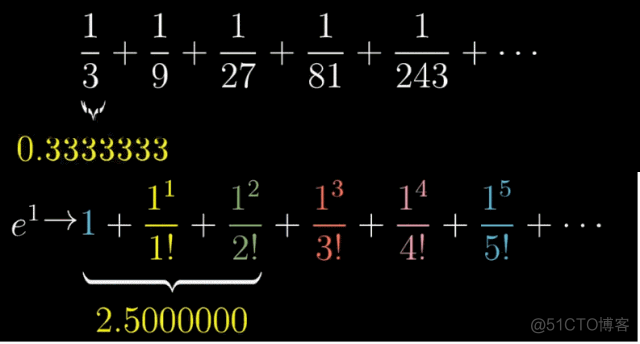

 

发散

与收敛相对应的，即发散，式子无法趋近于一个定值，比如ln(x)在x=1附近，如下图所示，虚线即为能够让多项式的和收敛的最大取之范围，称为【泰勒级数的收敛半径】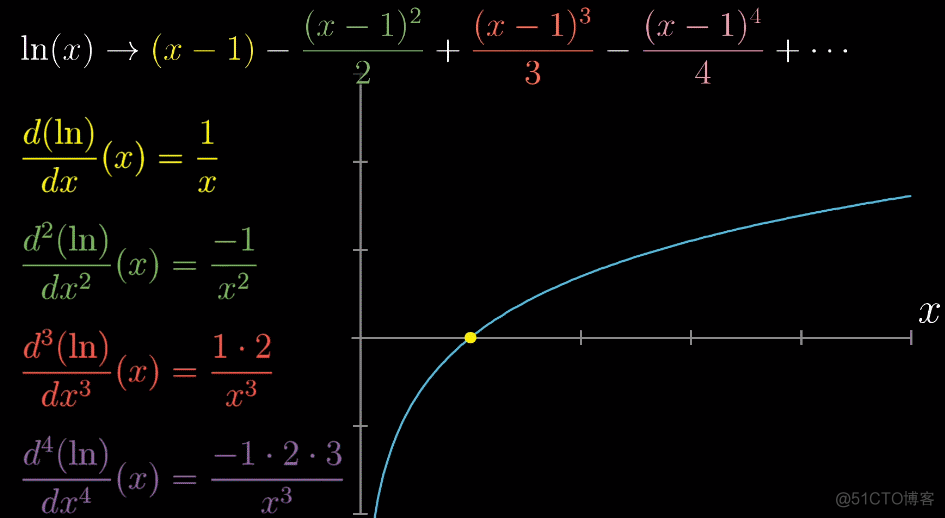

 

4

总结

泰勒公式干了一件什么事？

使用多项式表达式估计（近似） f(x)在x=a附近的值

泰勒公式的导数项如何推倒出来的？

某一点处的导数值信息<=>那一点附近的函数值信息

泰勒公式如何记永远不会忘？

参照第一条总结，是x=a附近公式 ➜ 多项式，很多项，要用求和写在一起；参照第二条总结，近似信息用的求导；系数就是对 x=a处求导一次一次放下来；OK，开始写！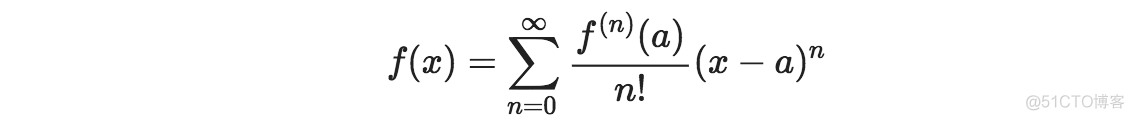

 

并不知道写的对不对，翻到上面Check。OK，很完美，收工！