R树--理解平面思维
R树数据结构
备注:参考wiki的内容。
简介
Guttman, A.; “R-trees: a dynamic index structure for spatial searching,” ACM, 1984, 14
R树在数据库等领域做出的功绩是非常显著的。它很好的解决了在高维空间存储数据,搜索等问题。
例如:
用手机查找附件商圈的所有餐厅。如果用经纬来记录餐厅的坐标(x,y), 这两个字段储存在数据库中。我们就需要遍历所有的位置信息,然后计算是否满足要求。如果是谷歌地图这种大数据库,遍历就太慢了。
R树解决了这种空间搜索问题。它把B树的思想扩展到多维空间,采用B树分割空间的思想,并在添加、删除操作时采用合并、分解结点的方法,保证树的平衡性。因此,R树就是一棵用来存储高维数据的平衡树。
wiki:
R树是用来做空间数据存储的树状数据结构。例如给地理位置,矩形和多边形这类多维数据创建索引。
人们发现它在理论和应用方面都非常实用[2]。
在现实生活中,R树可以用来存储地图上的空间信息,例如餐馆地址,或者地图上用来构造街道,建筑,湖泊边缘和海岸线的多边形。
然后可以用它来回答“查找距离我2千米以内的博物馆”,“检索距离我2千米以内的所有路段”(然后显示在导航系统中)或者“查找(直线距离)最近的加油站”这类问题。
R树还可以用来加速使用包括大圆距离[3]在内的各种距离度量方式的最邻近搜索[4]。
R树的原理
R树的核心思想:
聚合距离相近的节点,并在树结构的上一层将其表示为这些节点的最小限定矩形(minimum bounding Rectangle),这个最小外接矩形就成为上一层的一个节点。
例如,把平面上的R8,R9,R10这三个距离相近的节点,用一个矩形框起来,表示它们位于一个节点R3内,R3就是这3个节点的上层节点。
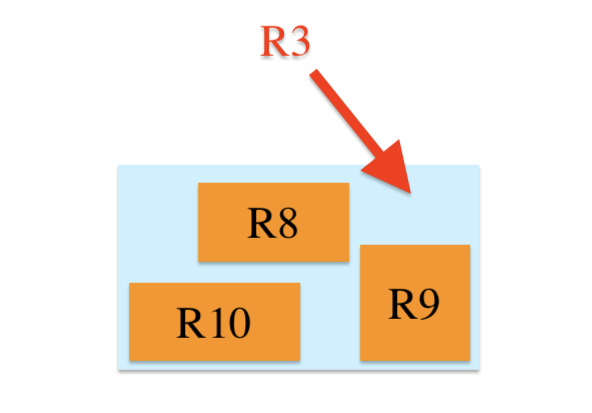
R树的“R”代表“Rectangle(矩形)”。因为所有节点都在它们的最小外接矩形中,所以跟某个矩形不相交的查询就一定跟这个矩形中的所有节点都不相交。
跟B树类似,R树也是平衡树(所以所有叶子节点都在同一深度)。它把数据按(内存)页存储,是为磁盘存储设计的(跟数据库的做法相同)。
跟其他树结构一样,R树的搜索算法(例如:交集,子集,最邻近搜索)也非常简单。方法是画出查询语句相应的边框,并用它来决定要不要搜索某个子树。
大部分关于R树的研究和改进都是关于如何改进建树的过程。它们可以分为两类,一类是如何从头开始构建一棵高效的树(被称为批量加载),另一类是如何在一棵已经存在的树上插入和删除。
R树不保证最坏情况下的性能,但是在现实数据[5]上一般表现不错。理论上来说,批量加载的优先级R树是最坏情况下的最优解[6],但由于复杂度太高,当前还没有在实际应用中获得关注。
数据结构
R树的数据按(内存)页存储,每一页存储多条数据,数据条数不超过一个事先定义的最大值,一般会多于最小值。
- 非叶节点上的每一条数据/记录的组成:指向子节点的标志符,该节点的外接矩阵。
- 叶子节点,用于储存每个对象需要的数据: 包括一个外接矩阵,和指向数据的标志符或数据对象本身 。
下面内容选摘自:https://www.cnblogs.com/cmi-sh-love/p/kong-jian-shud-ju-suo-yinRTree-wan-quan-jie-xi-jiJa.html
使用R树数据结构来建立空间数据模型
基于实体的模型(object based)
- 0维对象: 一般使用点point来表示不需要使用到形状信息的实体。
- 1纬对象或线状对象:用于表示一些路网的边,如道路。
- 2纬对象或平面对象:用于表示有区域面积的实体
常用的空间数据查询方法
- 窗口查询:给定一个矩阵,返回和查询矩阵相互重叠的物体。
- 点查询: 给一个点,返回包括这个点的所有几何图形。
空间数据的获取方法:
通常,我们不选择去索引几何物体本身,而是采用最小限定箱MBB(minimum bounding box ) 作为不规则几何图形的key来构建空间索引。
- 在二维的情况下,称为MBR(minimum bounding retangle)最小限定矩阵。
- 在三维的情况下,称为MBB(minimum bounding box)最小限定箱。
通过索引操作对象的MBR来进行查询
Filtering: 过滤掉MBB不相交的数据集,剩下的MBB被索引到的称为一个数据的超集。
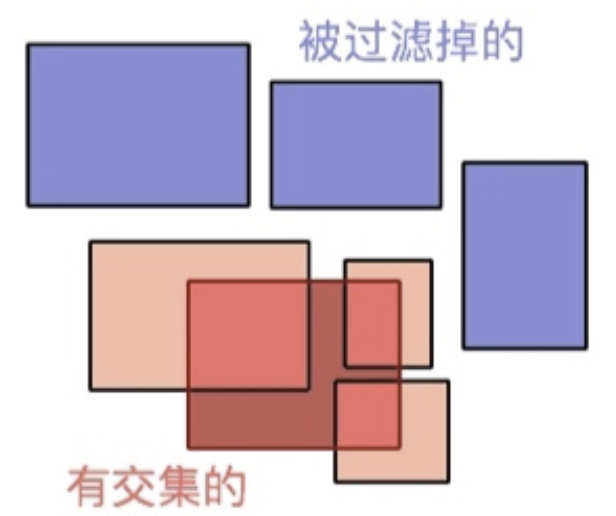
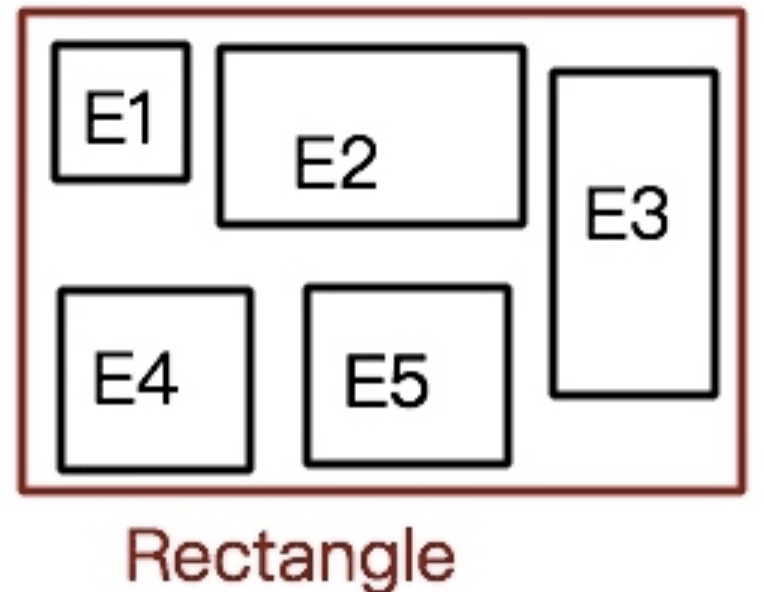
如何用数据表示一个MBR?
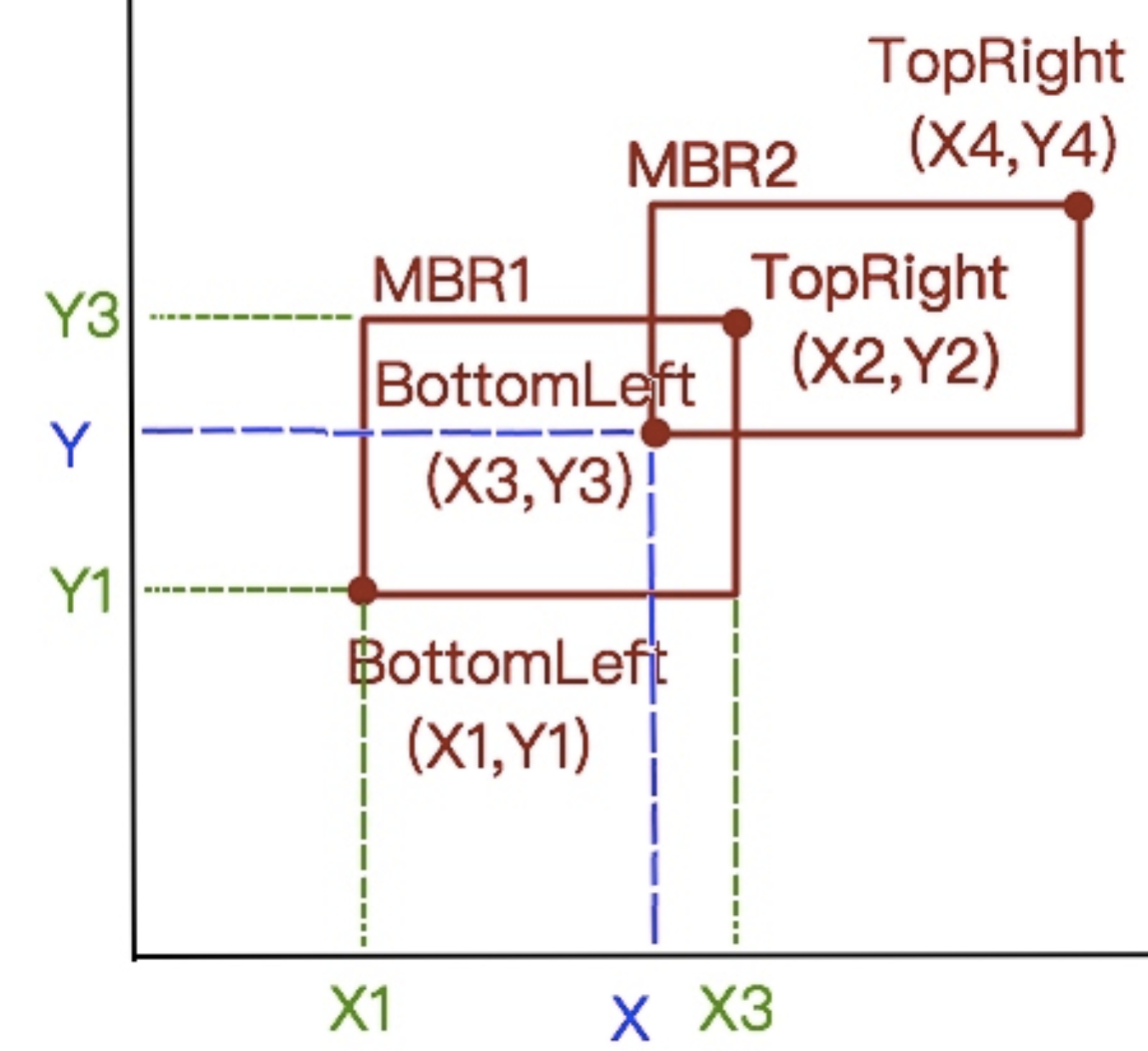
- 通常,我们只需要两个点就可限定一个矩形,也就是矩形某个对角线的两个点就可以决定一个唯一的矩形。通常我们使用(左下,右上两个点表示)或者使用右上左下,都是可以的。
#表示一个点的数据: public class Point{ #用一个类来表示一个点 public Float x; public Float y } #表示一个MBR的数据 public class MBR{ public Point BottomLeft; public Point TopRight; }
如何判断两个MBR是否相交?
如果一个MRB的角的坐标(x,y)位于另外一个MBR的范围内,就说明这两个MBR相交。
从B树到R树
B树是采用切分线段来缩小数据查询范围的一种思想,而R树是b树的多维版,R树也采用了B树的这一种分割的思想,
如果说线段的分割是一维的分割。那二维的分割就应该是区域的分割,而三维的就是几何空间的分割了。要注意的是R树并不只是二维空间数据的索引而已,它还可以索引三维甚至更高维。
R树的数据结构
R树是B树在高维空间的扩展,是一棵平衡树。每个R树的叶子结点包含了多个指向不同数据的指针,这些数据可以是存放在硬盘中的,也可以是存在内存中。
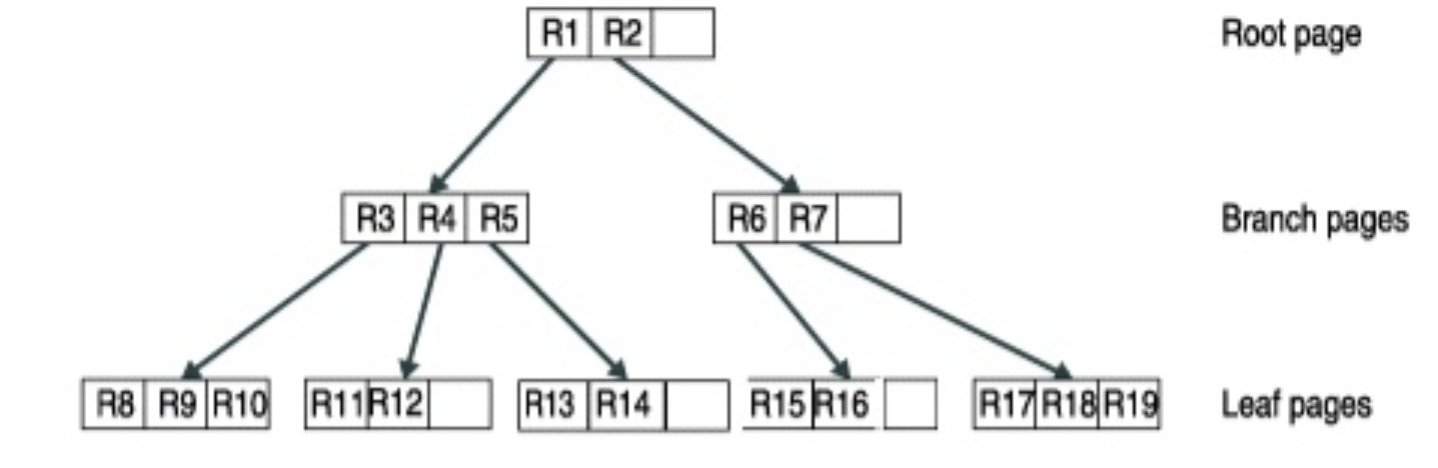
根据R树的这种数据结构,当我们需要进行一个高维空间查询时,我们只需要遍历少数几个叶子结点所包含的指针(即缩小到某个区域下去进行查询,还是采用缩小范围的思想),查看这些指针指向的数据是否满足要求即可。这种方式使我们不必遍历所有数据即可获得答案,效率显著提高。下图1是R树的一个简单实例:
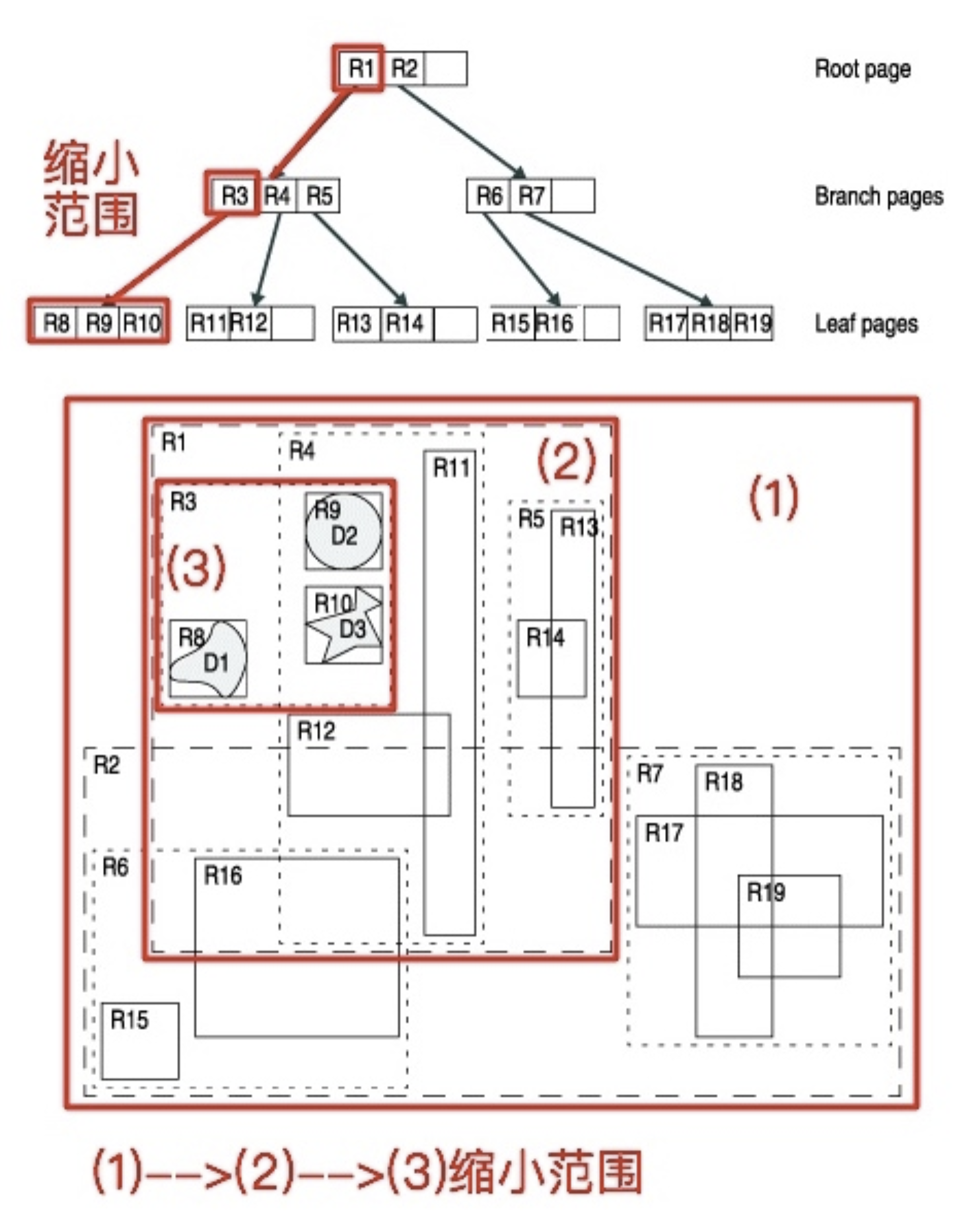
用地图的例子来解释,就是所有的数据都是餐厅所对应的地点,先把相邻的餐厅划分到同一块区域,划分好所有餐厅之后,再把邻近的区域划分到更大的区域,划分完毕后再次进行更高层次的划分,直到划分到只剩下两个最大的区域为止。要查找的时候就方便了。
下面就可以把这些大大小小的矩形存入我们的R树中去了。
- 根结点: 存放的是两个最大的矩形,这两个最大的矩形框住了所有的剩余的矩形,当然也就框住了所有的数据。
- 非根非叶节点:下一层的结点存放了次大的矩形,这些矩形缩小了范围。
- 叶节点: 每个叶子结点都是存放的最小的矩形,这些矩形中可能包含有n个数据。
R树的性质:
了解了数据结构,基本用途。下面总结它的性质。
R树有两个重要的属性: M和m。 其中M表示一个节点中条目的最大数量,而m小于等于M/2,表示一个节点中条目的最小数量。
- 每个叶节点,包括m~M个索引记录。根节点的记录可以少于m个。通常m = M/2。
- 叶节点的每个索引记录(条目),(I, 标志符),I是最小的可以在空间中完全覆盖这些记录所代表的点/矩阵。
- 每一个非根非叶节点(内部节点)有m~M个孩子节点。
- 每一个内部节点的条目(I, child-pointer),I是在空间上包括了在子节点中的矩形的最小矩阵。(类似性质2)
- 根节点如果不是叶节点(即整棵树,只有根节点自身),那么根节点至少有2个儿子节点。
- 所有叶子在同一高度,即R树是平衡树。
R树的操作
搜索:Search方法
R树的搜索操作很简单,跟B树上的搜索十分相似。它返回的结果是所有符合查找信息的记录条目。
B树输入的是数字符号,代表记录的位置。
而R树输入是什么?输入不仅仅是一个范围了,它更可以看成是一个空间中的矩形。也就是说,我们输入的是一个搜索矩形。
方法:
假设给定一棵R树,其根节点是T, 输入的参数是需要搜索的矩阵S,求S覆盖的所有索引记录?
两种情况:
- T是非叶子节点,如果T所对应的矩阵和S有相交,那么检查T的所有条目,确认每个条目的I是否和S相交。找到那些相交的条目(比如T1, T2都和S相交),然后继续检查T1,T2指向的子节点中的条目。一路向下,最终在叶节点上找到和矩阵S相交的所有的对象。这个过程就是反复调用Search方法的过程。
- T是叶子节点,如果T所对应的矩阵和S有相交,那么检查T的所有对象,找到和S相交的对象并返回这些对象。
如图:
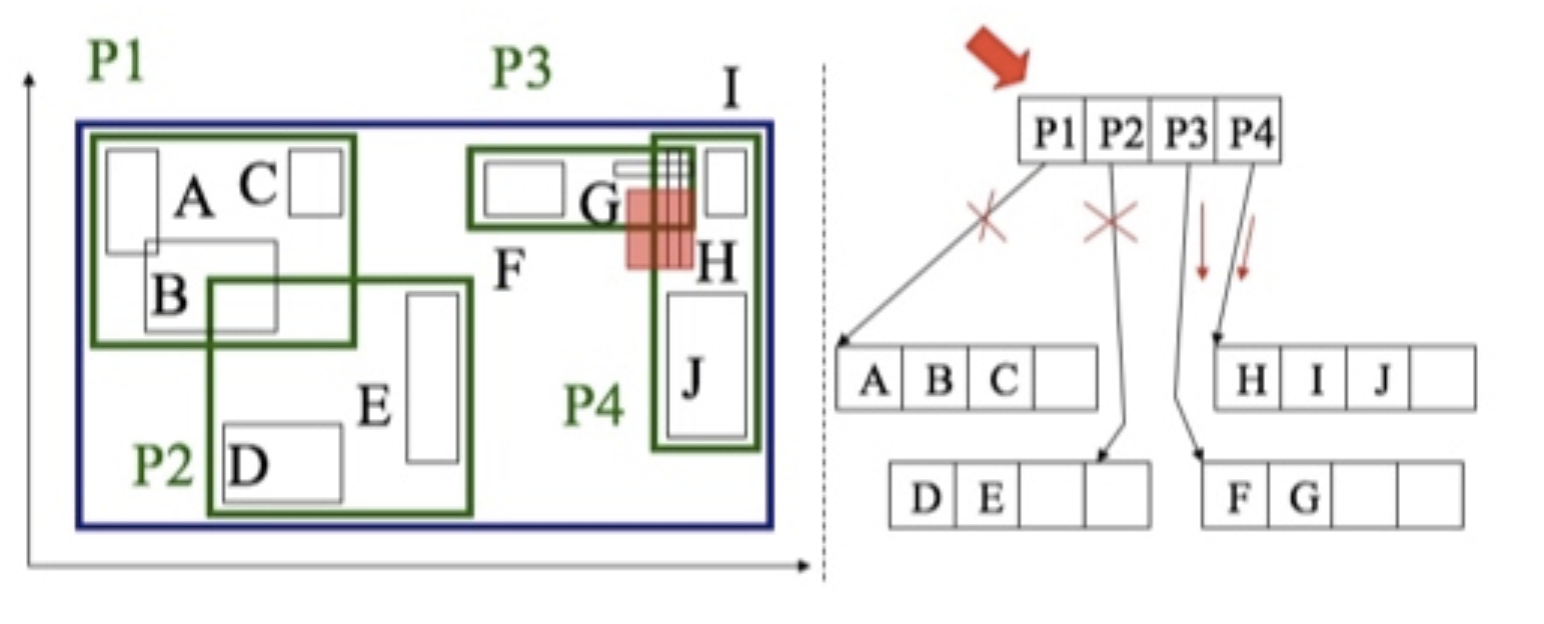
搜索矩阵是图中的红色部分S。通过坐标可以看出S和P3和P4相交。然后再遍历P3,P4所在子树就行了。
插入:Insert方法
R树的插入操作也同B树的插入操作类似。当新的数据记录需要被添加入叶子结点时,若叶子结点溢出,那么我们需要对叶子结点进行分裂操作。显然,叶子结点的插入操作会比搜索操作要复杂。插入操作需要一些辅助方法才能够完成。
把一个新的索引条目E插入一个R树内:
- 找到插入新记录的位置: 这里要调用Choose Leaf方法,选择一个叶节点L来存放E。
- 把记录E加入到叶节点中: 这里需要进行判断。
- 如果L有空间存放(即L的条目数量此时小于规定的最大值M),则加入E;
- 否则, 需要分裂,调用Split Node方法。把叶子节点L分裂成2个新节点L和LL(2个新节点包含了原来的L节点的所有条目和新条目E)。
- 向上传递变化:调用Adjust Tree方法对L节点操作。如果上一步是分裂操作,则对2个新节点调用Adjust Tree方法。
- 判断:是否树增高。如果节点的分裂导致了root的分裂,则需要生成新的root,并且让它的两个孩子节点为原来的root分裂后产生的2个节点。
方法Choose Leaf
- 初始化:设置N为根节点
- 检查叶子:如果N是叶子,返回N;否则下一步。
- 选择子树:设F为N的条目,F的矩阵I至少要放大到包含E的矩阵I。遍历N的所有条目,找到添加E.I时扩张最小的条目.
- 向下进行直达一个叶子:将N设为F,进行第2步操作。
方法AdjustTree
从一个叶节点 L 点上升到根,调整覆盖的矩阵。在传递变换的过程中可能会产生结点的分裂。
- 初始化:令N=L, 判断:如果L分裂过,则设NN为所得的第二个节点。
- 检查是否完成:如果N为根,则停止;否则,进行下一步。
- 调整N在父节点条目中的最小边界矩阵: 设P为N的父节点,E.N为N在P内的条目,调整E.N.I。让边界矩阵恰好包括了N的所有条目的矩阵。
- 解释⚠️因为N内的条目有了增减,所以要对N的边界矩阵进行调整,以重新包括它的所有条目的矩阵。
- 向上传递分裂:如果早先分裂出了NN,则创建一个新的条目ENN, 用ENN.pointer指向NN。ENN.I要包围NN中的所有矩阵。如果P还有空间,则ENN加入P。否则调用Split Node方法来生成P, PP(即把原来的P分裂)。
- 升高到下一级:令N=P。如果出现了一个分裂,则令NN=PP, 重复第2步骤。
插入条目的情况分类:
1. 有足够的空间插入的情况。即被插入的节点P有剩余空间容纳被插入条目X, 即P.E+1<=M。同时,X的区域面积(MBR)也位于P.I内。
2.需要增大MBR的情况。即被插入的节点P有剩余空间容纳被插入条目Y。但是,Y的MBR并不完全位于P的区域之内。因此要扩大P的MBR。
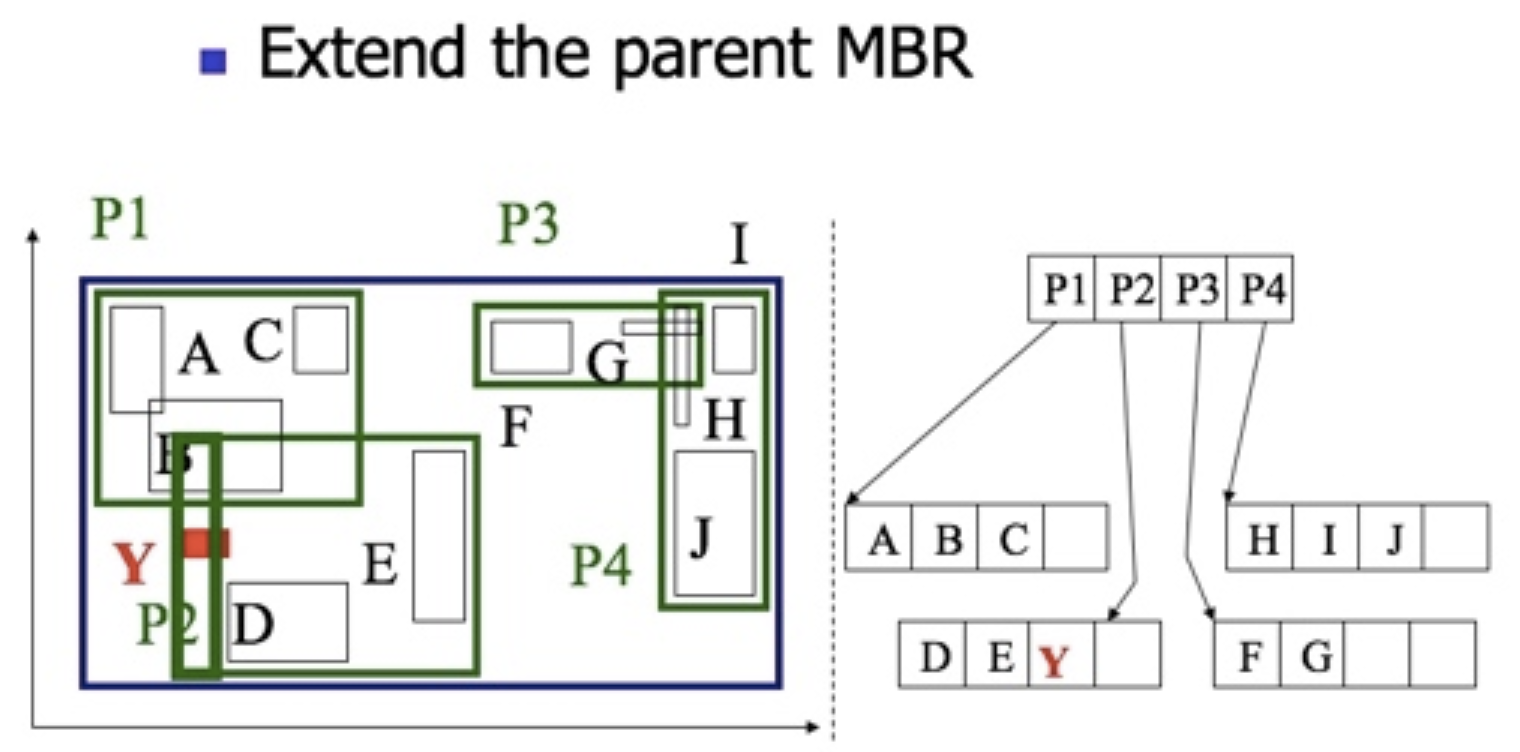
3.需要分裂的插入情况。由于插入的W的所在区域P的条目已经达到上限M。所有要分裂。
例子:P1,包括4个条目A,B,C,K。R树的设定阶m的最大值M等于4。所以插入W,就要分裂P1。
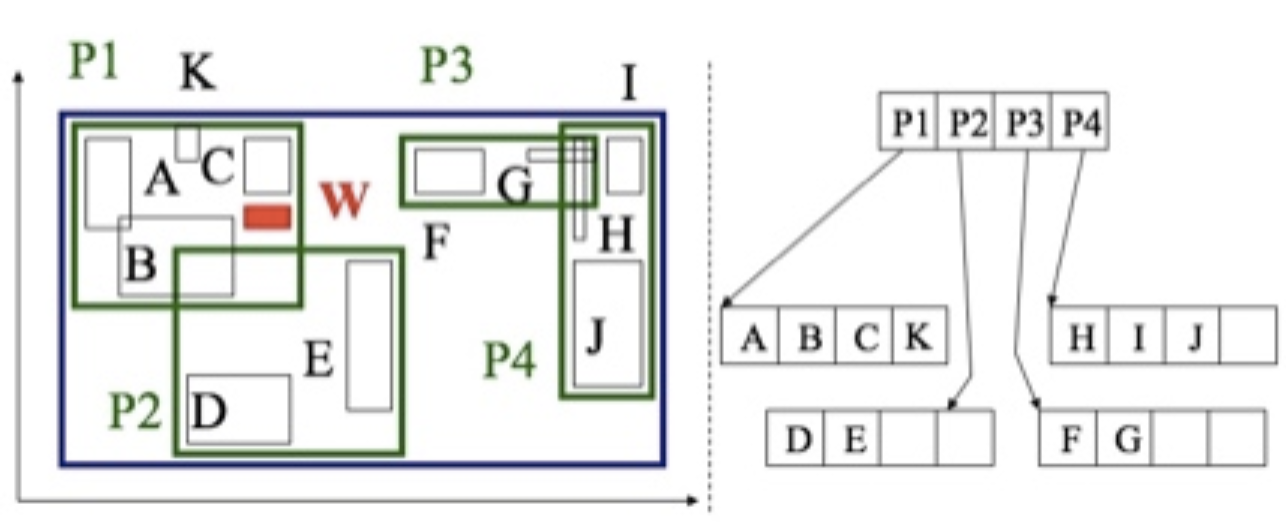
下面要讲的,就是关于节点的分裂。
算法:Split node方法
由上面已知,为了保持R树平衡,要求分裂节点。分裂必然导致时间上的花费,为了让算法更高效,大神们对节点的分裂,发明了许多方法,来优化分裂方法。

这个分配应按下述方法进行,尽量使两个新节点在接下来的搜索检查中不同时出现。因为访问一个节点取决于其覆盖的矩形所覆盖的搜索面积。两个覆盖矩形的总面积在一个分裂之后应为最小。
但,分裂的效果都不如R*树的算法好。可参考:https://dsa.cs.tsinghua.edu.cn/~deng/cg/project/2009f/2009f-2-f.pdf
具体代码可参考wiki:

