字符串匹配算法
字符串匹配算法
- 简介
- 暴力匹配
- kmp算法
- BM算法
- Sunday算法
首先是一系列概念定义:
- 文本Text: 是一个长度为n的数组T[1..n] (⚠️这里第一位置索引是数字1)
- 模式Pattern: 是一个长度为m的数组P[1..m], 并且m<=n.
- T和P的元素都属于有限的字母表Σ 表
- 概念:有效位移Valid Shift(用字母s代表)。即P在T中出现,并且位置移动s次。如果0<= s <= n-m ,并且T[s+1..s+m] = P[1..m],则s是有效位移。

上图的有效位移是3。
解决字符串的算法非常多:
朴素算法(Naive Algorithm)、Rabin-Karp 算法、有限自动机算法(Finite Automation)、 Knuth-Morris-Pratt 算法(即 KMP Algorithm)、Boyer-Moore 算法、Simon 算法、Colussi 算法、Galil-Giancarlo 算法、Apostolico-Crochemore 算法、Horspool 算法和 Sunday 算法等。
字符串匹配算法通常分为2个步骤:预处理和匹配。算法的总运行时间是两者之和。
下文举例:
- 朴素的字符串匹配算法(Naive String Matching Algorithm)
- Knuth-Morris-Pratt 字符串匹配算法(即 KMP 算法)
- Boyer-Moore 字符串匹配算法
朴素的字符串匹配算法(Naive String Matching Algorithm)
就是穷举法,枚举法,也叫暴力匹配。是最低效最原始的算法。特点:
- 无预处理阶段。(因为是暴力匹配)
- 对Pattern,可以从T的首或尾开始逐个匹配字母,比较顺序没有限制。
- 最坏时间复杂度O((n-m+1)*m).
方法是使用循环来检查是否在范围n-m+1中存在满足条件P[1..m] = T[s+1..s+m]的有效位移s。
伪代码:
Native_string_matcher(T, P) n <- length[T] m <- length[P] for s <- 0 to n - m do if P[1..m] = T[s+1..s+m] then print "Pattern occurs with shift"

Knuth-Morris-Pratt 字符串匹配算法(即 KMP 算法)
⚠️学习kmp算法的时候,很费了一番功夫,参考了多篇文章,主要是从知乎上获得灵感,一名网友建议先熟悉代码然后再理解原理。我是先看原理,但始终不能完全理解。后来改变方法,通过直接看代码,使用数据,最后理解了这个算法。
自己根据理论推导,但有些乱。 j == -1的判断是怎么来的? j = next_s[j] ,next_s是怎么来的?kmp是怎么利用的,用已有的代码倒推。 晚上,根据已有代码来理解,成功了。
这是对Pattern进行预处理的算法。
我的理解基本理解:
找到T中对P的第一次匹配,当P[1..(i-1)]等于T[1..(i-1)],但P[i]不匹配T[i]的情况,不使用使用穷举法,而是使用更优化的算法kmp,减少了不必要的字符比较。(⚠️这里指针i, 代表字符串中的第几个字符,不是数组的索引)
什么是“不必要的字符比较”?
因为P[1..(i-1)]成功在Text匹配,即和T[1..(i-1)]两个字符串相同。那么:
- 首先,确定T[1..i]的后缀集合和P[1..i]前缀集合。
- 然后,查看是否有两个集合的相交集合。
- 如果有,确认集合中那个最长的字符串max_string。
- ⚠️,max_string就是 P[1..(max_string.length)]。因此下轮再比较时,就无需比较这些字符了。
简单来说就是找到P[1..(i-1)]的前缀等于T[1..(i-1)]的后缀的字符串,这个字符串的字符,无需再比较。
这种算法比穷举法好太多了。
预先处理模式Pattern字符串
因此当已知字符串p时,先对它进行预处理。
理论:对p[1], p[1..2],p[1..i]..p[1..n]逐一处理(1<= i <=n),找到每个p[1..i]的前后缀相交的最长字符串,得到这个字符串的长度x。然后存入kmp数组。(但这样花费太多时间)
实际:求解Pattern的kmp或next_s的方法,使用的是递归的方法
由此得到一套字符串P的最大共有字符串的长度集合,即kmp数组。
例如:
下图给出了关于模式 P = “ababababca”的kmp(即前缀和后缀集合,共有的字符串集合中,最长的字符串的的长度的值)的表格,称为部分(即部分字符串)匹配表(Partial Match Table)。

计算过程
kmp[0] = 0,匹配a 仅一个字符,前缀和后缀为空集,共有元素最大长度为 0;
kmp[1] = 0,匹配ab 的前缀 a,后缀 b,不匹配,共有元素最大长度为 0;
kmp[2] = 1,aba,前缀 a ab,后缀 ba a,共有元素最大长度为 1;
kmp[3] = 2,abab,前缀 a ab aba,后缀 bab ab b,共有元素最大长度为 2;
kmp[4] = 3,ababa,前缀 a ab aba abab,后缀 baba aba ba a,共有元素最大长度为 3;
kmp[5] = 4,ababab,前缀 a ab aba abab ababa,后缀 babab abab bab ab b,共有元素最大长度为 4;
kmp[6] = 5,abababa,前缀 a ab aba abab ababa ababab,后缀 bababa ababa baba aba ba a,共有元素最大长度为 5;
kmp[7] = 6,abababab,前缀 .. ababab ..,后缀 .. ababab ..,共有元素最大长度为 6;
kmp[8] = 0,ababababc,前缀和后缀不匹配,共有元素最大长度为 0;
kmp[9] = 1,ababababca,前缀 .. a ..,后缀 .. a ..,共有元素最大长度为 1;
之后就可以利用这个表了。
具体使用这个表来匹配查找字符串的做法:
如果在j处发生不匹配,那么主字符串i指针之前部分与P[1..j-1]相同/匹配。通过求得的上面的表格可以找到j前面一位的kmp.
这共同的字符串就无需参加后续比较。j从新定位到这个字符串的后一位,和i比较。
具体流程是i不动,j指针指向P[1..j -1]字符串的共有字符串的后面一位,j = 4。然后下轮判断p[4] 是否等于 p[6].
例子:

图(a)在i位发生不匹配 (此时j = i = 6, j - 1 = 5),所以P[0..5] = "ababab"是和主string匹配的。找到了“ababab”的共有字符串是“abab”,就是图灰色部分。这部分字符串无需在之后比较了。
利用部分匹配表,可知kmp[5] == 4 ,进行下一轮匹配时,直接移动j指针到P[4],即j = kmp[j-1]从这里开始匹配,达到优化字符串的匹配/查找的目的。
另外,比较到发生不匹配时,需要在匹配表找kmp[j-1], 所以为了编程方便,将kmp数组向后移动一个位置,产生一个next数组, 使用这个next数组即可。⚠️这本身只是为了让代码看起来更优雅。无其他意义。反而对初学者来说,不好理解。
Ruby代码:
def Kmp_matcher(text, pattern) # 传入的text = "abababca",这里kmp已经给出。 kmp = [0,0,1,2,3,4,0, 1] i, j = 0, 0 while i < text.length && j < pattern.length if text[i] == pattern[j] i += 1 j += 1 else if j == 0 #第一个字符不匹配只能继续i++了, 就是穷举法了。 i += 1 else #使用kmp法, 即匹配失败,模式p相对于文本向👉移动。 j = kmp[j - 1] end end end if j == pattern.length # 返回pattern出现在text中的的位置。 return i - j else # pattern不匹配text return -1 end end
上面代码可知当pattern只有一个字母时,就是穷举法,所以i += 1。
优化代码使用next数组:
next[j]是什么?
next_s的意义:代表当前字符j之前的字符串中,有多大长度的相同前缀后缀(可称为最长前缀/后缀)。
例如:next[j] = k ,代表j之前的字符串中,最大前缀/后缀的长度为k。
本例子next_s = [-1, 0,0,1,2,3,4,0], 其实就是在kmp数组头部插入了一个元素-1, 或者说整体向后移动一个位置。
因为代码j = kmp[j - 1],所以使用j = next_s[j],但需要对第一个字符就不匹配的情况改代码:
特殊情况:
pattern只有一个字母"x"时,不匹配,我们设置next[0]等于-1。
当p = 'x', p[0]不等于text[0], 只能是穷举法了,每轮i+1,j不变。
因此要修改一下条件判断 : if j == -1 || text[j] == pattern[j]
- 因为j等于-1,所以判断true, 于是i和j都加+1。 那么下一轮i =1, j= 0, 继续比较。
- 当j = 0的情况时,如果不匹配,那么j = next_s[j] ,即j等于-1。 然后下一轮 , 又是true。
⚠️本质就是一个变通的方法,以适应next_s数组。见改后的代码:
def next_s_matcher(text, pattern) # 传入的text = "abababca" next_s = [-1, 0,0,1,2,3,4,0] i, j = 0, 0 while i < text.length && j < pattern.length if j == -1 || text[i] == pattern[j] i += 1 j += 1 else j = next_s[j] end end if j == pattern.length # 返回pattern出现在text中的的位置。 return i - j else # pattern不匹配text return -1 end end
⚠️有知乎网友说:先学AC自动机,就好理解kmp了。另外kmp也不是时间复杂度最好的算法。还可以优化。
那么最重要的问题来了,如何计算kmp或者next 数组?(可以使用代码递归的方法)
前面已经讲解了next[j]的意义👆。这里再强调一下:
next[j]的意义是什么?
j前面的匹配字符串是p[0..j-1], 它的前缀后缀集合的交集中,最长的字符串(最长前缀/最长后缀)的字符数就是next[j]。
(为了方便表示,在前缀集合中的这个字符串称为最大前缀,在后缀集合中的这个字符串称为最大后缀,它们是一样的。)
因此next[j]表示的就是
- 这个最大前缀/后缀的长度,
- 也表示了最大前缀的后面一位字符的索引。
先放上代码:ruby代码。
def getNext(pattern) pLen = pattern.length next_s = [] next_s[0] = -1 i = 0 # pattern的下标 j = -1 while i < pLen - 1 #只处理前PLen -1个字符的情况。所以是PLen - 1 if j == -1 || pattern[j] == pattern[i] i += 1 j += 1 next_s[i] = j else j = next_s[j] end end return next_s end
(代码好像很类似kmp的代码呵,但是看不懂。看了很多文章才慢慢理解。)
这个代码利用了递归的方法来得到next_s数组。
通过上面文章,我们知道最大前缀中的字符,无需再度匹配。因此下一轮匹配,文本字符串i不变,模式的指针j->最大前缀字符的后一位。
next的求解其实是对模式字符串自身的匹配比较,因此和kmp方法代码类似。
理解next的核心是理解if..else语句
假设开始新一轮循环,j等于6,i等于4,我们要判断p[6]是否等于p[4]
此时p[0..6]这个字符串是"ababab?"。“?”号代表要判断的p[6]。p[6]前面字符串的“ababab”是已经匹配成功的字符串,它的最大前缀/后缀是“abab”, max_len = 4。
现在"ababab"尾巴增加一个字符“?”,我们求这个“ababab?”的最大前缀/后缀的长度是多少?无需把前缀,后缀都列出来,然后找到它们的交集的笨方法。而是使用递归的方法:
想得到"ababab?"的最大前缀,我们要知道要"?"是什么字符,这里有2种情况:
第一种:(见图2)
如果“?”和"ababab"的最大前缀字符串的后一位字符相同,即“?” == "a", 那么 p[0..6]即"abababa"的最大前缀/后缀就是:“abab”+"a"。p[0..6]的max_len = 4 + 1 等于5。
可以看图2来增进理解,已知一个字符串pattern的最大前缀/后缀“abab”,如果pattern尾巴上增加一个字符"?",即pattern的长度加1, 那么pattern的最大前缀/后缀可能也会加1。这个可能实现的前提条件就是,恰好新增的字符等于最大前缀后面的第一个字符(p[i]==p[j])。即产生“新的最大前缀” == “新的最大后缀”。
这样就理解了if语句的前半部分:
if j == -1 || pattern[j] == pattern[i] i += 1 j += 1 next_s[i] = j else ...
# 如果pattern[j] 等于pattern[i],那么产生的新的最大前缀/后缀,其实就是之前的最大前缀+它后的一个字符。因此新的最大前缀/后缀长度+1.
# 即next_s[i] = j
另一种情况:(见图1)
本例子,不是"a", 那么这个字符串p[0..6]的最大共同字符串的长度不会增长,那么我们就要考虑新的最大共同字符串的长度和之前一样还是更小,甚至没有。
我们当然不会使用先把前缀和后缀的集合列出来,然后找共同的最长字符串,这是个笨方法。
在这里,我们用到了递归的方法。每轮比较,确定上一轮的最大前缀/后缀的最大前缀/后缀,是否是p[0..6]的最大前缀/后缀。
因此要向字符串头部移动指针j。让指针j指向最大前缀的最大前缀。
else j = next_s[j]
如下图2:两条红线的后一位比较不相等,那么就让红线1的最大前缀:绿线1的后一位和红线2的最大后缀黄线2的后一位p[i]比较。
还是不太理解,为何递归前缀索引j = next_s[j], 就能找到长度更短的相同前缀后缀?
假设新增的元素是p[i], 我们求的next[i]就是目的, 即找到p[0..i]的最大前缀/后缀(共同字符串)!
传统办法是找到前缀集合,后缀集合,然后找到其中的的共同字符串,可能有a, b, c 多个共同字符串,它们有2个特点:
- 长度比较:a < b < c。
- c的前缀后缀中共同字符串中最长的就是b。同理,b的最大共同字符串是a。
根据这个2特点我们可以使用递归的方法了:
我们在上一轮比较,已经知道p[0..i-1]的最大前缀, 这里设p[0..j-1] == p[i-j, i-1]。即共同字符串集合中的c。
前缀c+p[k]后缀c+"p[i]比较,发现二者不相同。
下一步就是前缀字符串b+它的后一位,和后缀字符串b+p[i]进行比较,二者不相等。
再下一步是前缀字符串c+它的后一位,和后缀字符串c+p[i]进行比较,二者还不相等。
最后一步,是p[0] 和p[j]比较,即字符串的第一个字符,和新增的尾巴字符比较。
通过一步步的递归,推导出p[0..i]有没有最大共同字符串。
由这个过程:我们发现了::
- 找p[0..i]的最大共同字符串的问题,其实就是,比较p[0..i-1]的共同字符串集合[a,b,c]的每个字符串的后一位,是否等于新加入的元素p[i]!
- 因为要找到最大的共同字符串,同时共同集合字符串的长度a<b<c,所以先比较c的后一位,判断不同后继续比较,最后比较首字符和新增尾字符。
因此,我们使用递归的方法,先比较p[i] 是否等于p[j] , 如果不相等则指针j指向当前前缀的前缀的后一位。并递归下去,直到得到一个结果。
图1:
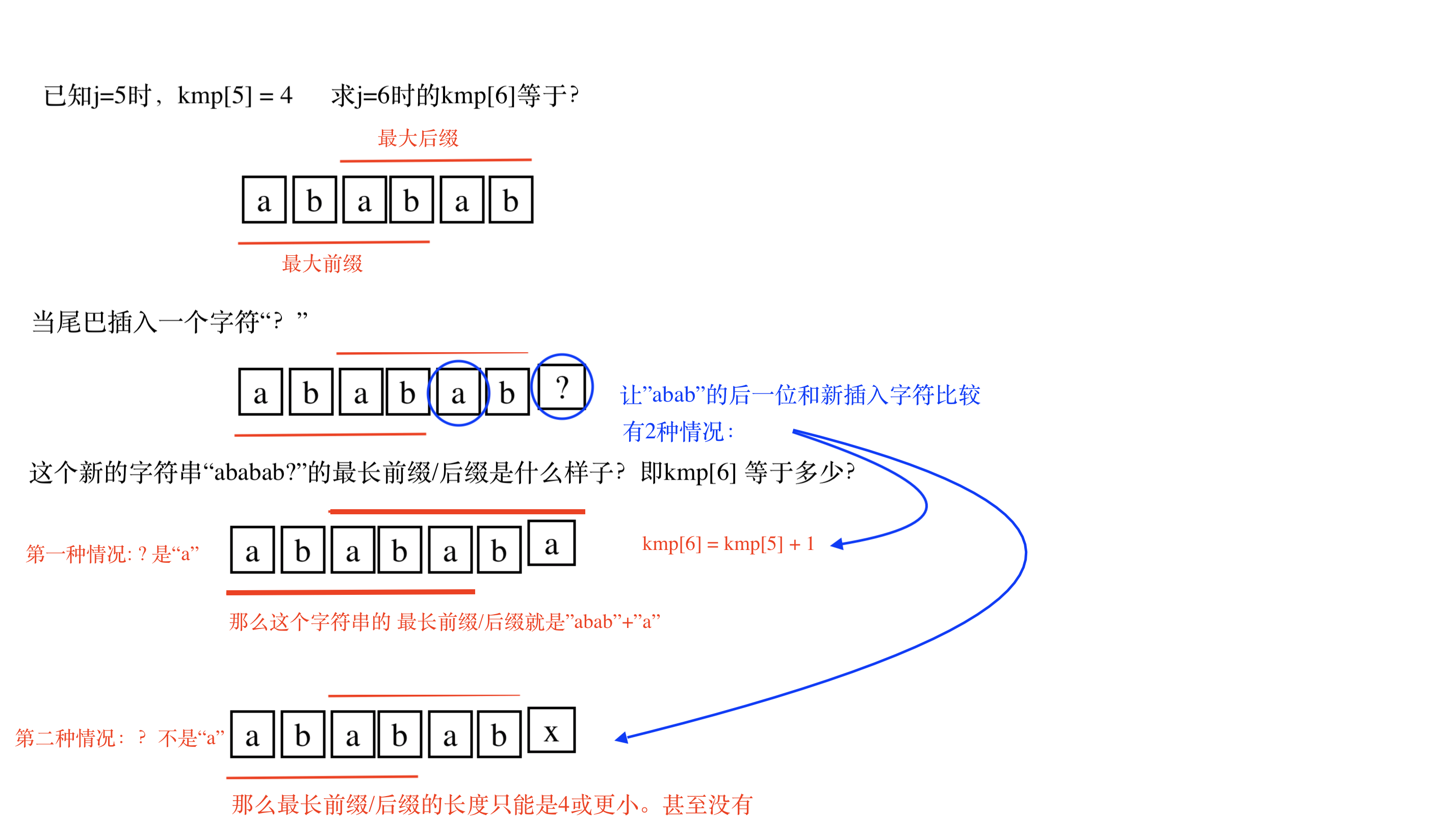
图2:
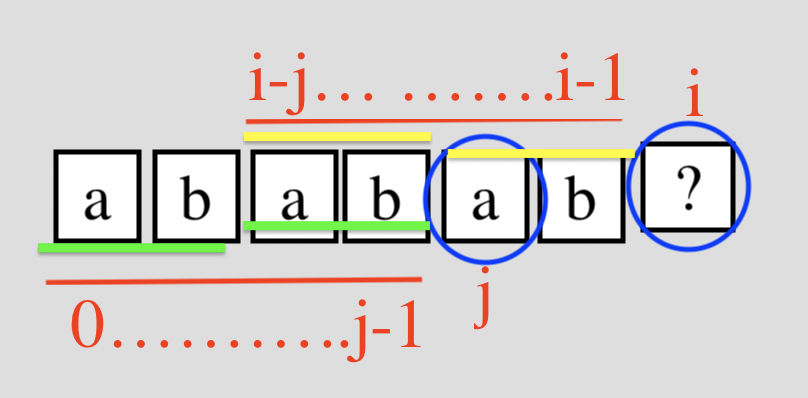
假设i和j的位置如上图,则next[i] = j ([0..j]的后一位字符的下标或者说是[0..j-1]的字符的数量)
区段 [0, i - 1] 的最长相同前后缀分别是 [0, j - 1] 和[i - j, i - 1],即这两区段内容相同。
按照算法流程,if (P[i] == P[j]),则i++; j++; next[i] = j;;若不等,则j = next[j],
- 即2个蓝圈的字符相等,判断true。
- 不等false。那么需要重新确定最长共有字符串的长度。j = next[j]。next[j]代表上图左下红线的字符串"abab"的最长前缀/后缀的长度。即2条绿线代表“abab”的前缀后后缀。j = 2。
- 然后再循环判断:if (p[i] == p[j])即p[2] ==p[6], 则next[6] = 2; 若不等, 则j = next[j]
- 其含义就是向字符串的前面找p[0..6]的“最大共同字符串”,每下一轮都是判断本轮最大前缀的最大前缀的字符串。
j 开始被赋值为-1, 是为了让next[0] = -1,但会导致:
- 程序刚开始时,使用p[i] ==p[j]判断,无疑p[j]会边界溢出。
- else语句中的j = next[j], j指针不断向字符串头部移动,当j被赋值-1时,溢出.
所以判断语句if上加上 j == -1。
对next数组的小优化
行文到此,已经理解了kmp算法的原理,和流程。
这里有一个小的优化,节省一步递归。情况是这样的:
如果遇到:text = 'abacababc', pattern = 'abab', 已经求得next_s = [-1,0,0,1],模拟流程:
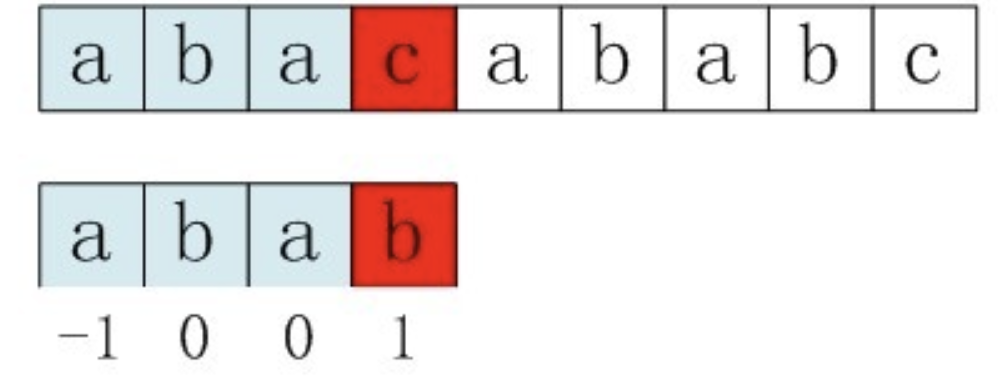
当j = 3, i =3时,比较发现p[3] 不等于t[3],于是j = next[j] ,即移动j到1,然后下一轮比较p[1]和t[3]是否相等。
结果发现仍然不相等。当然不相等啦!
观察一下,注意到,模式"abab",p[1]等于p[3],因此上面的一步递归后的再比较p[1]和t[3]完全没有比较。
既然已经知道如果p[1] == p[3], 那么下一步递归,和t[3]的比较同样不相同,就无需这一步的比较了,直接跳过去。
即在比较p[3]和t[3]后,直接进行2次递归。按照这个思路next_s[i]就储存2次递归后的值了:
if p[i] != p[j] next_s[i] = j else # 如果相等,则2次递归 next_s[i] = next[j] end
完全的代码见git:https://github.com/chentianwei411/-/blob/master/kmp.rb
kmp的时间复杂度分析
text长度为n,模式为m, 时间复杂度就是O(n+m)。
Kmp算法流程:
假设文本string匹配到i位置,模式串pattern匹配到j位置:
- 如果j == -1, 或者s[i] == p[j],则令i, j都➕1。继续匹配下一个字符。
- 如果上面的判断都false, 则i指针不变,j指针移动到next[j]。即匹配失败的话,pattern相对于string向右移动了j-next[j]位置。
因为匹配成功,则i+1,j+1,匹配失败则i不动,整个算法最坏的情况是i移动到终点,仍然模式不匹配文本。所以花费时间是线性的O(n)
再加上预处理模式串的时间O(m), 最坏时间复杂度是O(n+m)
BM算法
1977年,德克萨斯大学的2名教授发明了一种新的字符串匹配算法:BM算法。(和kmp一样,也是以名字命名)。
最坏时间复杂度是O(n),。 比kmp算法更高效。
参考阮一峰http://www.ruanyifeng.com/blog/2013/05/boyer-moore_string_search_algorithm.html
特点是模式串从左向右比较。(比BM算法还早的Horspool算法也是这样。)
两个规则:
- 坏字符规则:当文本串中的某个字符跟模式串的某个字符不匹配时,我们称文本串中的这个失配字符为坏字符,此时模式串需要向右移动,移动的位数 = 坏字符在模式串中的位置 - 坏字符在模式串中最右出现的位置。此外,如果"坏字符"不包含在模式串之中,则最右出现位置为-1。
- 好后缀规则:当字符失配时,后移位数 = 好后缀在模式串中的位置 - 好后缀在模式串上一次出现的位置,且如果好后缀在模式串中没有再次出现,则为-1。
Sunday算法
http://www.voidcn.com/article/p-gcxakovf-sg.html
比kmp算法快的算法非常多,而且比kmp更好理解。kmp的确是很折磨新手。
Sunday算法由Daniel M.Sunday在1990年提出,实际上比BM算法还快。
Sunday算法是从前往后匹配,在匹配失败时关注的是主串中参加匹配的最末位字符的下一位字符。
- 如果该字符没有在模式串中出现则直接跳过,即移动位数 = 模式串长度 + 1;
- 否则,其移动位数 = 模式串长度 - 该字符最右出现的位置(以0开始) = 模式串中该字符最右出现的位置到尾部的距离 + 1。
参考:
参考了不少文章,有的太复杂有的太简单。还是推荐知乎上的这个https://www.zhihu.com/question/21923021
和这篇https://subetter.com/algorithm/kmp-algorithm.html
扩展章节摘录:https://blog.csdn.net/v_july_v/article/details/7041827


 浙公网安备 33010602011771号
浙公网安备 33010602011771号