Trie树(代码),后缀树(代码)
Trie树系列
- Trie字典树
- 压缩的Trie
- 后缀树Suffix tree
- 后缀树--ukkonen算法
Trie是通过对字符串进行预先处理,达到加快搜索速度的算法。即把文本中的字符串转换为树结构,搜索字符串的速度提高。
Trie树
Trie这个术语来自于retrieval。检索的意思。
Tire树,又叫字典树,前缀树,单词查找树或键树。从名字来看,就能大概了解它的用途了。专门用于处理字符串匹配的数据结构,用来解决在一组字符串集合中快速查找某个字符串的问题。
它是一种有序树,多叉树,用于保存关联数组,关键字通常是字符串,但是它不直接存在于某个节点,而是存在于一条路径上。
因为一个节点的所有子节点都有共同的关键字,所以Trie树也叫做前缀树(Prefix Tree)。
例子:
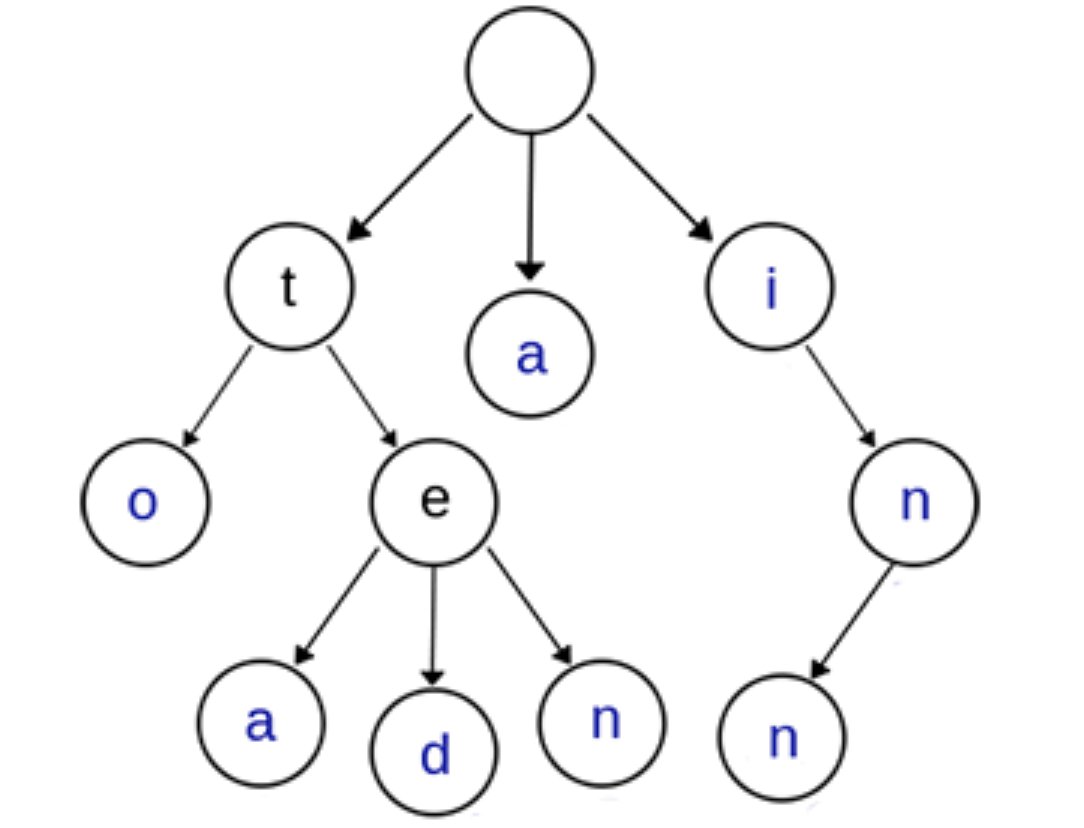
上图是一棵Trie树,表示了关键字集合{“a”, “to”, “tea”, “ted”, “ten”, “i”, “in”, “inn”}
从中可看出特点:
- 根节点不包含字符,即空字符。根节点外的每个子节点都有一个字符。
- 从根节点到某一个节点,路径上经过的字符连接起来,为该节点对应的字符串。
- 每个节点的子节点包含的字符互不相同。
通常在实现的时候,会在节点结构中设置一个标志,用来标记该结点处是否构成一个单词(关键字)。
核心思想:
利用字符串的公共前缀来减少无谓的字符串比较以达到提高查询效率的目的。
优点:
- 插入和查询效率是O(m), m是字符串的字符数量。
- Trie树中不同的关键字不会产生冲突。
- Trie树不用求 hash 值,对短字符串有更快的速度。通常,求hash值也是需要遍历字符串的。
- Trie树可以对关键字按字典序排序。
缺点:
-
当 hash 函数很好时,Trie树的查找效率会低于哈希搜索。(不理解⚠️)
-
空间消耗比较大。
Trie树的应用:
具体来说就是经常用于统计和排序大量的字符串(但不仅限于字符串),所以经常被搜索引擎系统用于文本词频统计。它的优点是:最大限度地减少无谓的字符串比较,查询效率比哈希表高。
1.前缀匹配:
trie树常用于搜索提示。如当输入一个网址,可以自动搜索出可能的选择。当没有完全匹配的搜索结果,可以返回前缀最相似的可能。
还有如各种通讯录的自动补全功能等。
2字符串检索:
给出 N 个单词组成的熟词表,以及一篇全用小写英文书写的文章,按最早出现的顺序写出所有不在熟词表中的生词。
检索/查询功能是Trie树最原始的功能。给定一组字符串,查找某个字符串是否出现过,思路就是从根节点开始一个一个字符进行比较:
- 如果沿路比较,发现不同的字符,则表示该字符串在集合中不存在。
- 如果所有的字符全部比较完并且全部相同,还需判断最后一个节点的标志位(标记该节点是否代表一个关键字)。
3.词频统计:
虽然也可以用hash做,但是如果内存空间有限,就不行了。这里我们就可以用trie树来压缩下空间,因为公共前缀都是用一个节点保存的。
Trie树的局限性
如前文所讲,Trie的核心思想是空间换时间,利用字符串的公共前缀来降低查询时间的开销以达到提高效率的目的。
所谓的空间,是指每一个字符都要单独开辟一块储存空间,并使用指针指向它。因此空间开销大增。但这种结构带来了查询效率的提升,这就是空间换时间。
假设字符的种数有m个,有若干个长度为n的字符串构成了一个 Trie树 ,则每个节点的出度为 m(即每个节点的可能子节点数量为m),Trie树 的高度为n。很明显我们浪费了大量的空间来存储字符,此时Trie树的最坏空间复杂度为O(m^n)。也正由于每个节点的出度为m,所以我们能够沿着树的一个个分支高效的向下逐个字符的查询,而不是遍历所有的字符串来查询,此时Trie树的最坏时间复杂度为O(n)。
这正是空间换时间的体现,也是利用公共前缀降低查询时间开销的体现。
Trie树在空间上也是有优化策略的,比如对部分前缀或者后缀进行压缩,这样以来能够节省不必要的指针存储,这种实现需要更复杂的编码来支持。
Ruby实现的T树的插入,查找,和删除
代码使用的是数组来存储所有的子节点。
最新版本的代码见git
class T_tree attr_accessor :root def initialize @root = Trie_node.new() @root.children = [] #用于储存根节点的孩子节点 end #词频统计,给空树插入一个单词,如果第2次又插入这个词,就会发现重复,然后count+1. def insert(next_child = @root, word) # 判断传入的字符串的第一个字母是否存在于当前节点的孩子内。 exist_node = try(next_child.children, word[0]) if exist_node # 继续判断node[1]是否在exist_node节点的儿子们中: if word.size == 1 #如果待插字符串只剩最后一个字母,证明这个单词没有后续了。 # 词出现频率统计: exist_node.count += 1 #因为当前节点是一个词的最后的字符,所以加1. return else # 重复使用insert方法(),传入剩下的字符 insert(exist_node, word.slice(1..-1)) end else # "当前节点的孩子中不包括#{word[0]},插入#{word}" i = 0 size = word.size while i < size next_child = _insert(next_child, word[i]) # 词频统计:在插入的单词的最后生成的叶节点中:count+1 if i == (size -1) next_child.count += 1 end i += 1 end end end # 字符串检索:查找单词是否已经存在于树中,如果不存在则打印 def find(word) if _find(word) puts "#{word}存在于库中" else puts "#{word}不存在" end end def delete(word) if _find(word) puts "#{word}存在于库中, 是否删除它? > true" if _delete(word) == true puts "删除成功" else puts "不能删除前缀词" end else puts "#{word}不存在" end end private def _find(next_child = @root, word) exist_node = try(next_child.children, word[0]) if exist_node # 只剩最后一个字母 if word.size == 1 return true else # word还有多个字母,继续查找比较。 return _find(exist_node, word.slice(1..-1)) end else return false end end def _delete(next_child = @root, word) exist_node = try(next_child.children, word[0]) # 已经比较完最后一个字母 if word.size == 1 #如果当前节点有儿子,则不能删除它。 if exist_node.children.size != 0 #"不能删除前缀单词!" return false else exist_node = nil return true end else # word还有多个字母,继续查找比较。 if _delete(exist_node, word.slice(1..-1)) == true exist_node = nil else return false end end end def try(childen, x) childen.each do |c| if c.node == x return c end end return false end def _insert(node, letter) new_node = Trie_node.new(letter) node.children << new_node return new_node end end class Trie_node attr_accessor :count, :node, :children def initialize(node = "") @node = node @count = 0 #记录从根节点到这个节点的,共走了多少次。 @children = [] end end
摘录和参考:
https://juejin.im/post/5c2c096251882579717db3d2
https://blog.csdn.net/lisonglisonglisong/article/details/45584721
https://en.wikipedia.org/wiki/Trie
https://blog.csdn.net/StevenKyleLee/article/details/38343985
https://blog.csdn.net/johnny901114/article/details/80711441 推荐👌。
压缩字典树
参考:https://sqh.me/tech/search-in-large-string-data-by-using-trie-and-compressed-trie/
由于使用树+指针实现Trie树非常耗用内存,所以可以将原始Trie树进行压缩,即只有单个子节点的节点可以合并成一个节点(一个孤立的string)。
the space of complexity空间复杂度,就可以从O(m*n)降低到O(n)。
Suffix Trees
后缀树提出的目的是用来支持有效的字符串匹配和查询,例如上面的问题。后缀树(Suffix tree)是一种数据结构,能快速解决很多关于字符串的问题。后缀树的概念最早由Weiner 于1973年提出,既而由McCreight 在1976年和Ukkonen在1992年和1995年加以改进完善。
参考
https://www.cnblogs.com/gaochundong/p/suffix_tree.html。
https://www.oschina.net/translate/ukkonens-suffix-tree-algorithm-in-plain-english
理解3点:
- 对字符串匹配的算法分为两个步骤:Preprocessing和Matching。算法的总运行时间是2者之和。
- 字典树系列:是对文本text进行预先处理Preprocessing,即把文本储存在树结构内。
- 除此之外,有对匹配Matching进行预先处理的算法: KMP字符串匹配算法,Boyer-Moore字符串匹配算法。
后缀树可以从字典树推导出来:
- 根据文本生成所有后缀的集合。
- 将每个后缀作为一个单独的关键词,形成字典树,然后压缩字典树,就是后缀树。
例如banana这个词,首先生成6个后缀,然后每个后缀作为一个词,形成字典树,然后压缩便成了后缀树:
banana
anana
nana
ana
na
a
图例子,这是使用字典树的方式来创建出后缀树:
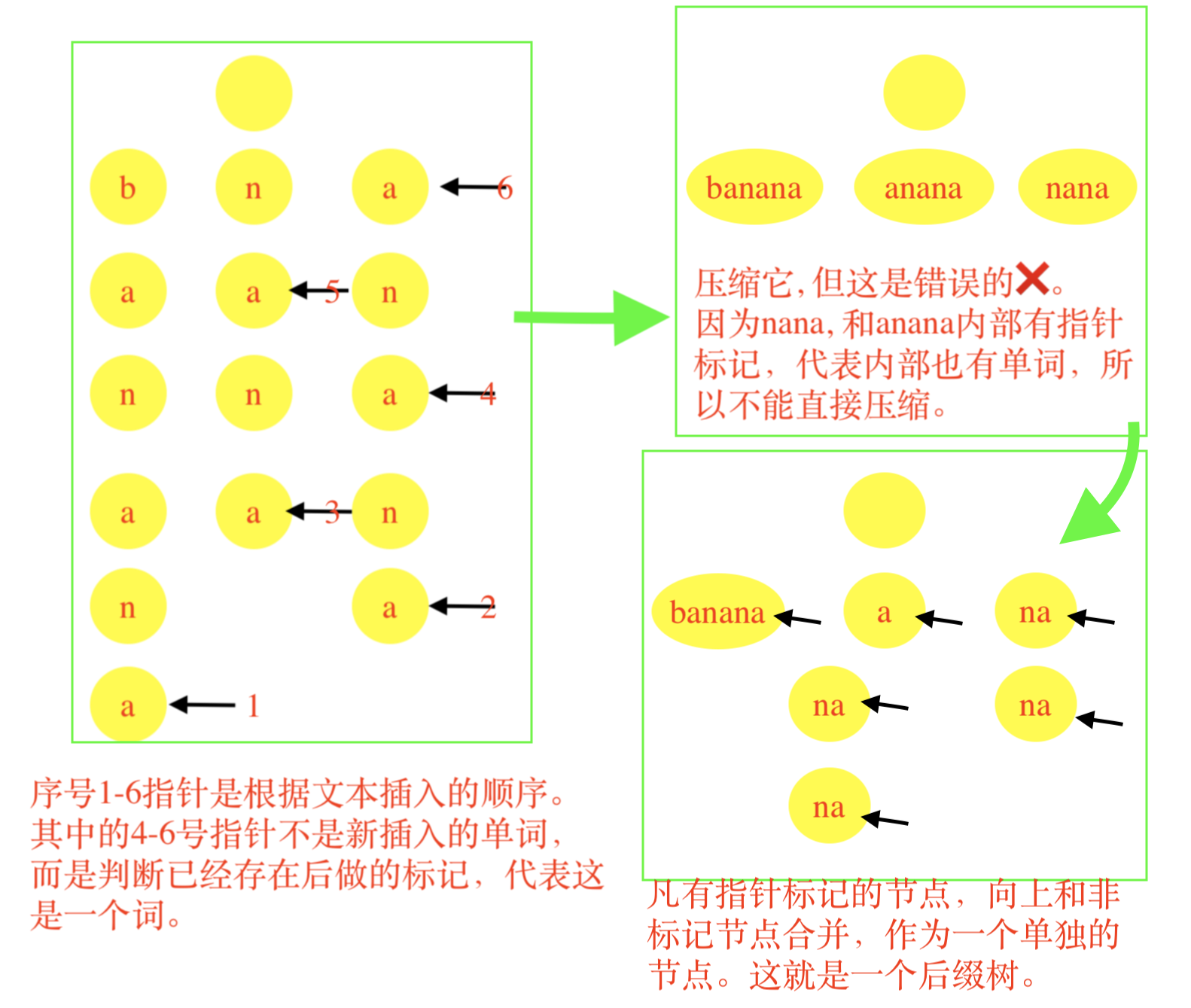
需要注意⚠️的是,这个算法使用字典树的方法逐个插入后缀词, 但注意后缀树是根据text中的字符数量,创建出后缀词,一下增加了大量工作量:
5个字符的单词,插入字典树,插入时间5
5个字符的单词,形成后缀词5个,字符插入时间 1 + 2 + 3+ 4 +5 = 15
所以长度为m的字符串创建一个后缀树的时间复杂度是O(m + (m -1) + (m - 2) + .. + 1),在实际数据挖掘应用中,对大规模的数据集,效率太低了。所以下面介绍Ukkonen的算法。
后缀树之Ukkonen的算法
首先要说明显式后缀树(Explicit Suffix Tree)和隐式后缀树(Implicit Suffix Tree)两个概念。
我的理解:
“banana”, 有6个后缀,可以从根节点出发,生成6个子节点,这就是显式。
但是可以看到anan,na, a,三个后缀,正常字典树不会这么分出来,因为anan和a 其实是“anana”的前缀,na是“nana”的前缀,所以会放到banana, anana内,方法就是做个标记,代表它们是后缀,这就叫隐式。
在 1995 年,Esko Ukkonen 发表了论文《On-line construction of suffix trees》,描述了在线性时间内构建后缀树的方法。
他优化了时间复杂度到O(n)
基本原理
这个算法工作的步骤,从左到右,对字符逐个操作。
字符串的每个字符都是一个步骤。每一步都可能涉及到多个个体的操作,但是我们将会看到(见结尾最后的观察)的总数量操作是O(n)。
我的理解:
这个算法的本质就是:用储存字符在字符串的索引(index/指针)来代替储存字符本身。
用边存储字符串的2个字符的索引。即这个边的首字符和结尾字符的索引。
结尾字符永远用是#表示,因此知道这条边[i, #],就知道其后缀词是什么了。
假设插入字符串"abc", 使用#作为标记,代表一个后缀词。
第一步骤:操作“a”。
边[0, #] , 即a
第二步骤:操作“b”。
插入一条新的边来表示“b”:[1, #]。
- ⚠️边[0,#]因为存的是对字符串“abc”的索引,自然就自动表示了后缀词"ab",而新插入的边[1, #]则表示后缀词"b"。
- 每条边的空间复杂度是O(1), 即只是使用了2个指针(索引)而已。
第三步骤:操作“c”。
插入一条新的边来表示“c”, [2, #]。同样之前的2个边自动的代表了后缀词"abc"和"bc"
- 经过以上3个步骤的操作,得到了"abc"的后缀树。
- 步骤次数等于字符串的字符数量。
- 每个步骤只是插入了一条新的边,这条边的数据包括2个指针。因此每步骤的时间复杂度是O(1)。
- 因此,对应一个长度为n的Text,总计需要O(n)的时间构建后缀树
第一次扩展:简单的重复
上面的字符串并没有重复,如果是"banana"之类的字符串,算法如何处理?以下面的字符串举例:
abcabxabcd
前3个步骤和上文相同。
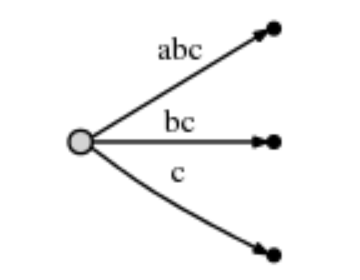
第四步骤:操作“a”。
此时就不是插入新的边了,而是在已存边中查看是否有重复的字符。
⚠️我的理解:
向树内插入“a”, 它是隐式后缀词。
因此不开辟新边,树结构表面上不改变。后缀词“a”所在的边仍然只储存2个指针:即代表from和to。
为了表示实际的变化,引入新的三元变量active point和变量remainder = 1
为了更好的说明算法,引入了2组概念:
- 活动点active point:包括(active_node, active_edge, active_length)
- 剩余后缀数remainder: 一个整数,代表下一步需要插入多少个新的后缀
简单的说:
- 对于上面的"abc"的例子,活动点总是(root, '0x', 0),即活动节点是根节点,活动边是空字符指定的边,活动长度是0。每次插入新的边是从root开始的.
- 在每个步骤开始时,剩余后缀数(remainder)总是 1。意味着,每次我们要插入的新的后缀数目为 1,即总是最后一个字符。
到第3步结束: #为3, active_point = (root, '\0x', 0), remainder = 1 (⚠️代表下一步要插入的后缀数是1,因为每次只插入一个字符)
现在将有变化了,当我们给根节点插入当前最后一个字符a的时候,我们特别注意到已经存在一条以a开始的边:abca。在这种情况下我们做如下工作:
- 我们不向根节点插入一条新边[4,#]。相反,我们只是注意到后缀a已经在我们的树里。我们还是保留🌲原来的样子。
- 设置活动点为(root,'a',1)。这意味着: 活动点现在从root开始,活动边是以'a'开头的某个边,位置就在这个边的第1位。
- 我们还增加了剩余后缀数, 那么在下一步骤开始的时候,剩余后缀数为2。
#为4, active_point = (root, 'a', 1), remainder = 2, (后缀"a"和下一个待插入字符)
⚠️当要插入的后缀已经存在于树中,实际上这颗树结构没有发生改变,我们只是修改了变量active point和remainder。
⚠️remainder表示下一步要插入的后缀数量!!!
第五步骤:操作“b”。
同样树结构不变,“#”后移,它在字符串的位置为5。
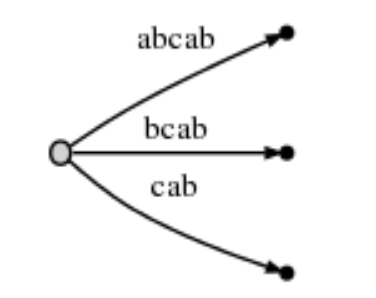
在第4步完成后,remainder为2,表示此时要插入的后缀数量为2。即有了2个后缀"a"->"ab"和新增的"b"。
它们是隐式插入的。因为没有插入新的边“b”。"ab"隐藏于"abcab"内。在“bcab”内隐藏着“b”.
- 修改活动点的active_length为2。指“abcab”中的前2个字符a和b.
# = 5, active_point = (root, 'a', 2), remainder = 3, (下一步待插后缀:“ab” , "b", 和下一步插入的字符)
第六步骤:操作“x”。
因为remainder为3, 所以后缀是“ab”->"abx", "b"->"bx", "x"三个后缀。
6-1: ‘abx’
从活动点三元组可知是从“a”开始的边。
所以,在“ab”后插入x。但是,当前树还不存在"x", 所以分裂边"abcabx", 插入一个内部节点:
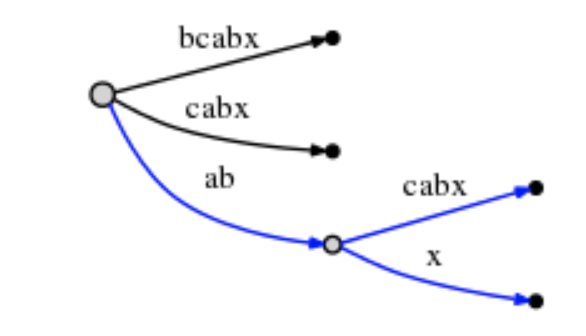
相当于分裂并插入一个新的边,其中代表x的边[5, #],耗费O(1)时间。
此时完成处理"abx"后缀。
6-2将处理“bx”, 因此需要修改活动点:
- active point不变root
- 活动边是“b”开始的这条边“bcabx”,因此赋值active_edge = "b",
- 同时因为“b”->"bx",当前active_length = 1。
- 6-1处理了一个后缀“abx”所以还剩下2个后缀要处理。remainder 减 1。
# = 6, active_point = (root, 'b', 1), remainder = 2
这里总结出rule1:
Rule 1
当向根节点插入时遵循:
active_node 保持为 root;
active_edge 被设置为即将被插入的新后缀的首字符
active_length 减 1;
6-2: ‘bx’
然后是插入新增后缀"bx"。
根据活动点三元组(root, "b", 1)知道活动边"bcabx", 然后判断“x”是否在第一个字符“b”后面,如果判断已经出现则结束当前步骤,但是此时判断的结果是“x”没有出现在第一个字符"b"之后,所以分割这条边并插入"x":
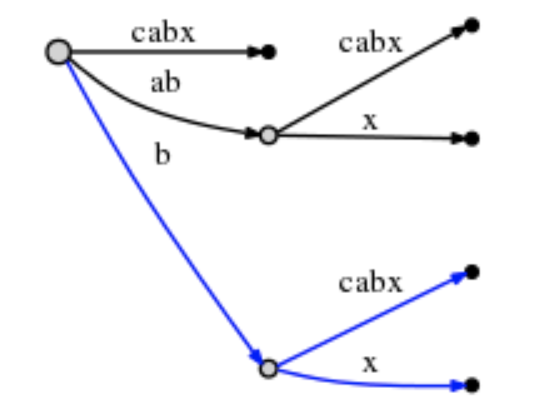
然后更新活动点:
- 包括活动边改为"x",
- 活动长度改为0 (这里我对active_length理解是,‘x’后面没有字符,所以长度为0), 也是根据rule1。
- remainder减去1
# = 6, active_point = (root, 'x', 0), remainder = 1
这里总结rule2:
Rule 2
如果我们分裂(Split)一条边并且插入(Insert)一个新的节点,并且如果该新节点不是当前步骤中创建的第一个节点(边),
则将先前插入的节点与该新节点通过一个特殊的指针连接,称为后缀连接(Suffix Link)。后缀连接通过一条虚线来表示。
⚠️通过观察后缀链接,相互关联的的这两棵树,的结构是一样的!
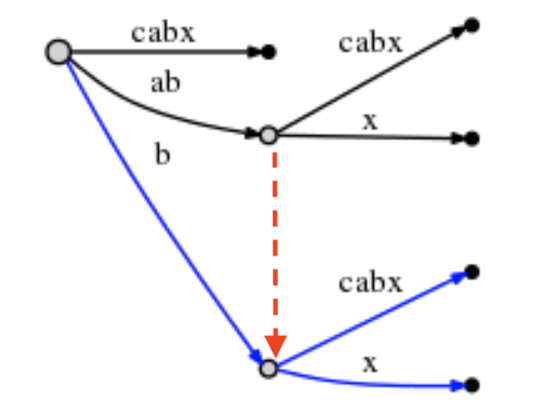
6-3: ‘x’
最后处理"x"后缀。通过活动点三元组,插入“x”后缀。因为没有以"x"为前缀的边,所以在root上插入新的边。
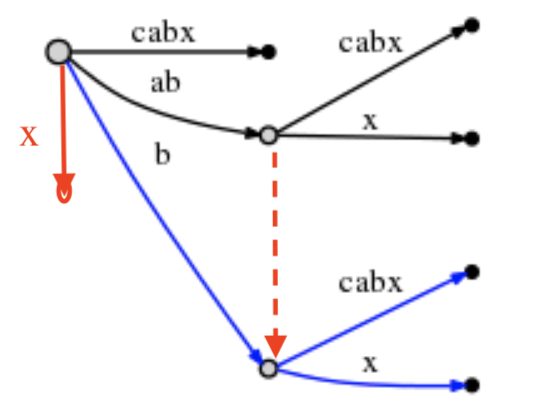
这样完成了第六步骤的所有操作。更新活动点,此时的活动点就是最原始的空边。
# = 6, active_point = (root, '\0x', 0), remainder = 1
此时字符串“abcabxabcd"还有“abcd”4个字符未做处理,继续:
第七步,处理"a"
"#"向后移动一个位。发现“a”已经存在,因此只更新活动点和remainder:
# = 7, active_point = (root, 'a', 1), remainder = 2
第八步,处理"b"
类似第七步,发现新增后缀"ab"和"b"都已经存在于树中了。更新活动点和remainder:
# = 8, active_point = (root, 'a', 2), remainder = 3
第九步,处理"c"
“#”继续后移动一位置。此时remainder等于3,所以需要插入"abc" ,"bc", "c"三个后缀。“c”存在于“ab”边后分裂的边“cabx”。所以只更新活动点和remainder:
- 活动边"cabxabc"不再和root相邻,所以活动节点active_node改为node1, 即"ab"边指向的点。
- 活动边的第一个字符“c”,所以active_edge改为c。
- 活动长度改为1。
- remainder + 1
# = 9, active_point = (node1, 'c', 1), remainder = 4
所有叶节点都自动更新了,见图:
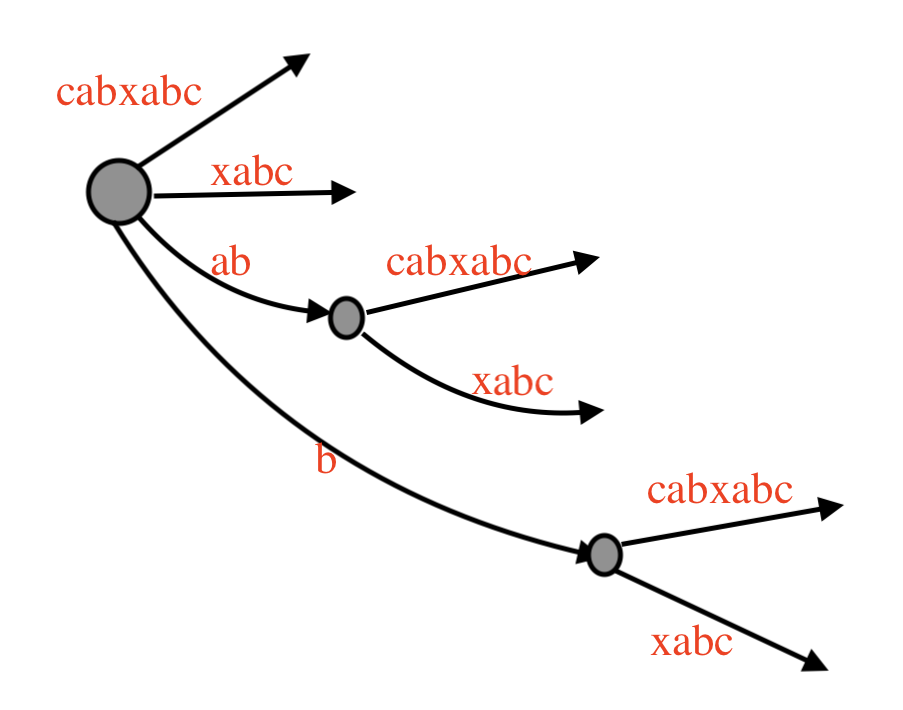
第十步,处理最后一个字符“d”
"#"继续后移动。此时remainder等于4,需要处理"abcd", "bcd", "cd", "d"。
10-1: “abcd”
根据活动点三元组(node1, 'c', 1)
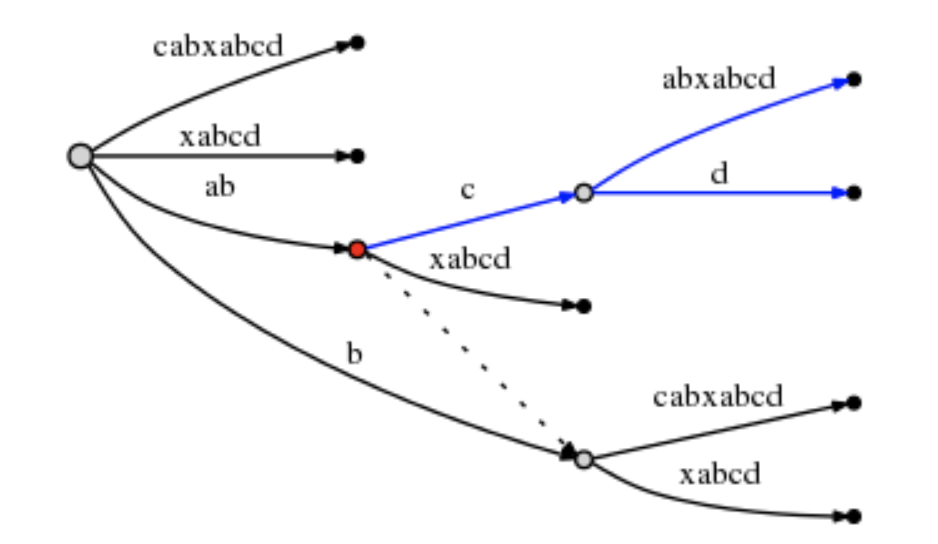
⚠️此时分裂的是"cabxabcd"这条边,它不和root直接相邻,而是和node1连接。
下面操作后缀“bcd”, 因此变更active_point:
- 活动节点为“b”边指向的节点。设置为node2。这是也是后缀连节指向的节点。
- 活动边为node2节点后“c”所在的边。
- 活动长度为 1. (我的理解是其实就是增加了d. 'bc'->"bcd")
- 因此处理了“abcc”,所以remainder - 1。
# = 10, active_point = (node2, 'c', 1), remainder = 3
此时总结rule3:
Rule 3
当从 active_node 不为 root 的节点分裂边时,我们沿着后缀连接(Suffix Link)的方向寻找节点,
如果存在一个节点,则设置该节点为 active_node;
如果不存在,则设置 active_node 为 root。active_edge 和 active_length 保持不变。
10-2: “bcd”
由上面的active point可知,要分裂“后缀链接指向的节点”的后面的边“cabxabcd”。形成新的节点并插入边“d”。
根据rule2:
因为分裂这条边并插入一个新的节点,并且10-2是第十步中创建的第2个节点(10-1分裂并插入了"d"), 不是第一个节点。
可以观察到第十步骤创建的两个节点其实是完全一样的结构。
所以在第一个节点 上建立一个后缀指针,指向第二个节点。代表它们是一样的结构。
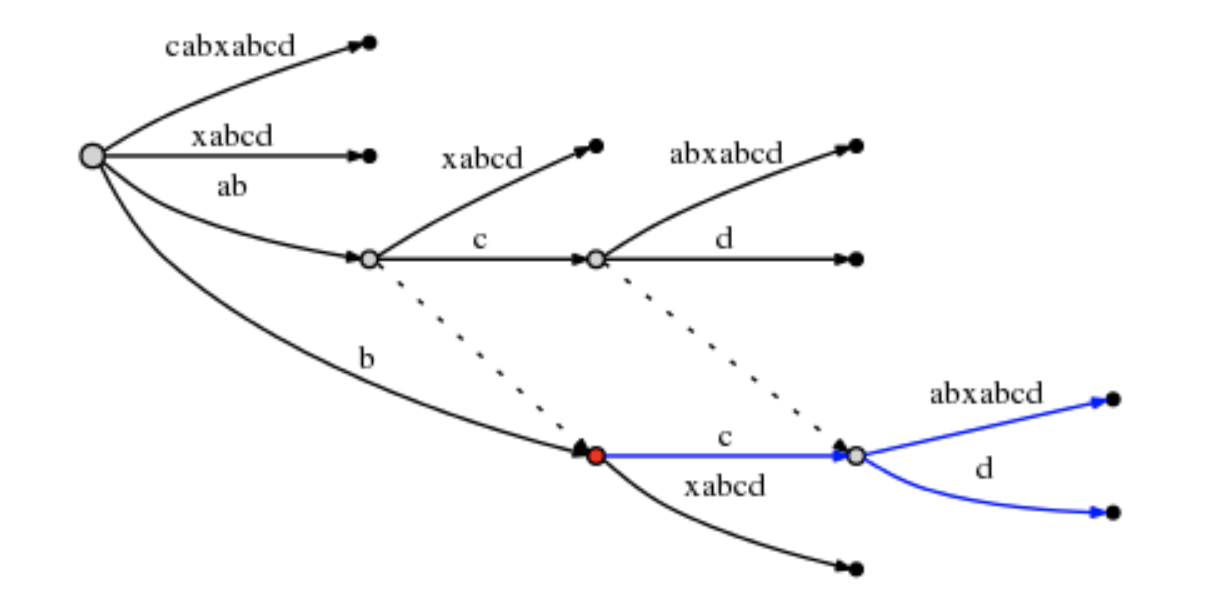
下一步10-3将处理"cd"后缀,变更活动点:
- "cd"从root上找,活动节点active_node = root,活动边为“c”所在的边。
- 边长active_length = 1。
- remainder -1
# = 10, active_point = (root, 'c', 1), remainder = 2
10-3: “cd”
如此又创建了一个新的内部节点,插入了一条边"d"
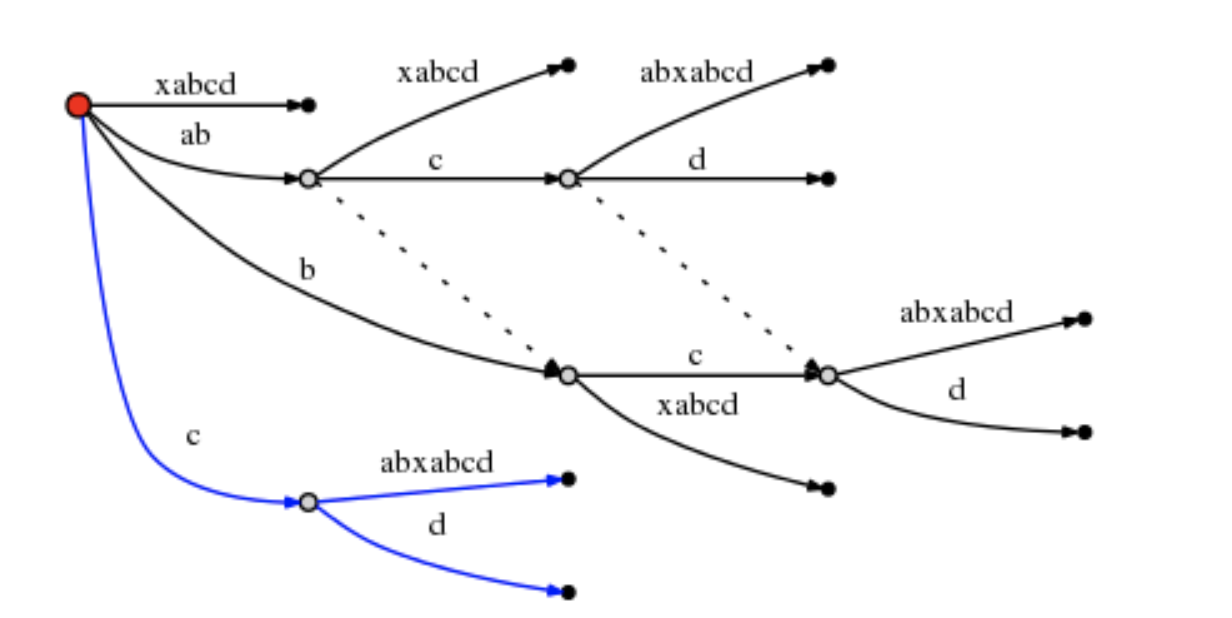
还是根据rule2法则:
10-3分裂并插入的新节点,需要和10-2分裂并插入的节点连接起来。即在10-2创建的节点上,新建一个指针(后缀连接)。
我的理解:后缀指针从10-1到10-2到10-3形成一个链表。代表它们创建的节点后的🌲树结构是一样的。
变更active point, 即在root上插入一条新边"d", 因此要使用法则Rule1
- 当向根节点插入时遵循: active_node 保持为 root; active_edge 被设置为即将被插入的新后缀的首字符; active_length 减 1;
同时remainder -1
# = 10, active_point = (root, 'd', 0), remainder = 1
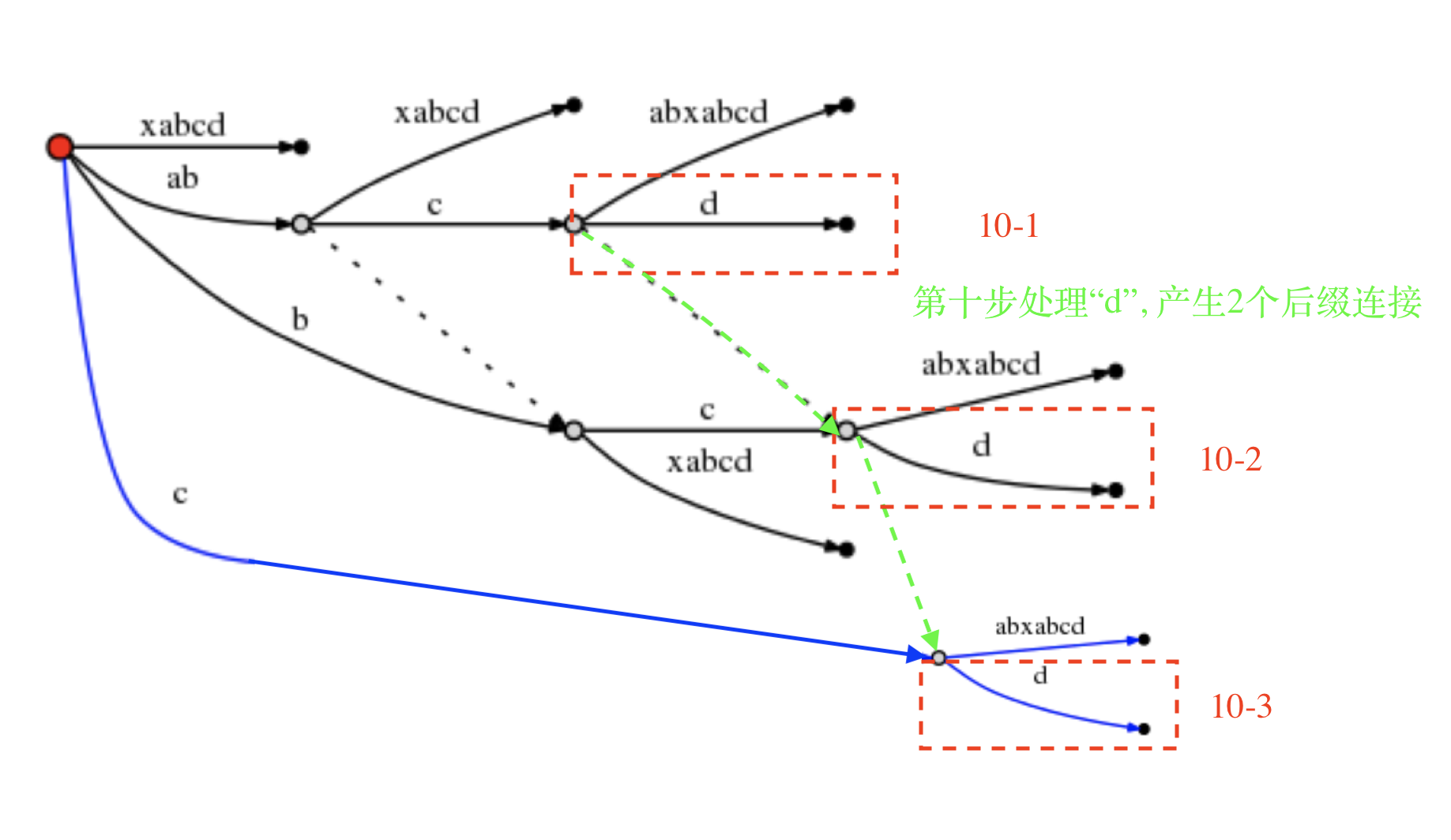
10-4: “d”
插入新边“d”, 第十步骤完成。后缀树完成。
当前活动点改为(root, "\0x", 0)即从root出发的空边。
总结:
- 每一步中将#右移1位,所有的叶节点自动更新。
- 但实际上未处理2种情况:从前一步骤遗留的后缀remainder, 当前步骤的最终字符。
- remainder 告诉了我们还余下多少后缀需要插入。这些插入操作将逐个的与当前位置 "#" 之前的后缀进行对应, 需要逐一处理。每次处理时间O(1),active point三元数组告诉我们从哪改。
- 每次插入之后,remainder减少1。
- 如果存在Suffix Link则连接到下一个节点。(见上面的图)。
- 如果不存在,则返回root节点(rule3)
- 如果已经是root节点,则根据rule1来修改活动点。
- 上面的情况都需要O(1)时间。
- 如果在插入操作中,发现要插入的字符已经存在于树上,则无需做什么。这叫做隐式后缀。这些后缀会在未来处理。
- 那么如果在算法结束时 remainder > 0 该怎么办?这种情况说明了文本的尾部字符串在之前某处已经出现过。此时我们需要在尾部添加一个额外的从未出现过的字符,通常使用 "$" 符号。这就是标记。表示它是一个叶节点。代表这是一个后缀。因为在已经完成的后缀树查找后缀时,会遇到隐藏后缀,这不是真正的后缀,所以用$加以区别。
- 同时,最后也强制 remainder = 0,以此来保证所有的后缀都形成了叶子节点。
- 总体的复杂度为 O(n)。如果Text的长度为n, 则又n次插入操作,再加上“$”,则为n+1步骤
- 这是因为,每一步骤,有2种情况:
- 执行插入, 处理所有的remainder,每次处理花费时间O(1)。
- 要么不插入,树结构不变,只记remainder + 1。
- remainder相当于本次插入操作留待后面的步骤处理。因此,总体插入操作还是n, 因此时间复杂度是O(n)。
Github的代码:C语言写的https://gist.github.com/axefrog/2373868
后缀树的应用:
对字符串的查找,匹配。
- 查找字符串Pattern是否在字符串Text内:
- 使用Text构造后缀树,使用字典树搜索字符串的方法搜索Pattern即可。如果存在,则Pattern必然是Text的某个后缀的前缀。
- 计算指定字符串 Pattern 在字符串 Text 中的出现次数
- 用 Text+'$' 构造后缀树,搜索 Pattern 所在节点下的叶节点数目即为重复次数。如果 Pattern 在 Text 中重复了 c 次,则 Text 应有 c 个后缀以 Pattern 为前缀。
备注:
本文自用学习,主要但不限于这篇博文:https://www.cnblogs.com/gaochundong/p/suffix_tree.html
