平衡搜索树-B树。
B Tree 系列
摘录:
https://blog.csdn.net/v_JULY_v/article/details/6530142
动态查找树有: 二叉查找树,自平衡的二叉查找树系列(如avl,红黑树,左倾红黑树),2-3树,2-3-4树,B树系列。树的高度和查找效率高度相关。
但在大规模数据储存中,二叉查找树等必然高度增加,造成磁盘i/o读写过于频繁,导致查询效率下降。
因此采用多叉树通过降低树的高度提高效率。B树系列就是通过保持较低的高度从而避免磁盘过于频繁的查找存取操作。
wiki:https://en.wikipedia.org/wiki/B-tree
B树
相比于内存, 访问磁盘/磁带等块设备时, 大块数据读写有更好的性能。
为高效使用这类设备, 尽量将多份数据放入一个盘块block中,同一磁道中。就可以提高读写信息时的查找时间。
B树是解决此问题的算法统称。
应用:
B树(或其变形)广泛应用于有大量元数据需要保存到外部存储介质的应用场景, 例如文件系统, 数据库, 以及存储自精简/压缩/重删等特性中.
B树与红黑树有相似的地方:一棵含n个结点的B树的高度也为O(lgn),但可能比一棵红黑树的高度小许多,应为它的分支因子比较大。
B树与红黑树最大的不同在于,B树的结点可以有许多子女,从几个到几千个。
所以,B树可以在O(logn)时间内,实现各种如插入(insert),删除(delete)等动态集合操作。
B树中的每个结点根据实际情况可以包含大量的关键字信息和分支(当然是不能超过磁盘块的大小,根据磁盘驱动(disk drives)的不同,一般块的大小在1k~4k左右);
这样树的深度降低了,这就意味着查找一个元素只要很少结点从外存磁盘中读入内存,很快访问到要查找的数据。
wiki
B树(英语:B-tree)是一种自平衡的树,能够保持数据有序。这种数据结构能够让查找数据、顺序访问、插入数据及删除的动作,都在对数时间内完成。
B树,多叉树,平衡多路查找树。一个节点可以拥有2个以上的子节点。B树可以看作是2-3查找树的一种扩展。当m等于3时,就是2-3树。当m等于2时,就是2叉搜索树。
定义
B树的阶(英语对应order)定义是不统一。wiki
1. 最开始定义是在一个非根节点中,key的最小值。对这个定义后人有异议。
2. Knuth (1998,)order为孩子们的最大数量(比key的最大值大1) defining the order to be maximum number of children (which is one more than the maximum number of keys).
所以按照Knuth定义一棵m阶的B树:(国内教材所用的定义)
- Every node has at most m children.
- 每个节点最多有m个孩子。
- Every non-leaf node (except root) has at least ⌈m/2⌉ child nodes.
- 非叶非根节点至少有[m/2]个儿子。[m/2]表示取大于m/2的最小整数。
- The root has at least two children if it is not a leaf node.
- 根节点至少有2个儿子。除非它本身是叶子节点,即整棵树只有它一个节点。
- A non-leaf node with k children contains k − 1 keys.
- 非叶节点:有k个儿子,就有k-1个keys。
- All leaves appear in the same level and carry no information.
- 所有叶子节点在同一层,不携带信息data。
- ⚠️增加一条:非root节点的key的数量是[m/2]-1至m-1。
内部节点
通常代表一个orderd set of element(这里指的是key和它对应的data组成一个记录/元素)和孩子节点的指针。
data表示key对应的条目在硬盘上的逻辑地址。
每个节点包含n个关键字信息:(n, p0, k1, k2,...Kn, Pn)
- Ki(i=1..n)是关键字,⚠️关键字对应一个data。
- Pi是指向子树的指针,并且Pi-1所指向的儿子内的所有key都小于Ki,但大于K(i-1)
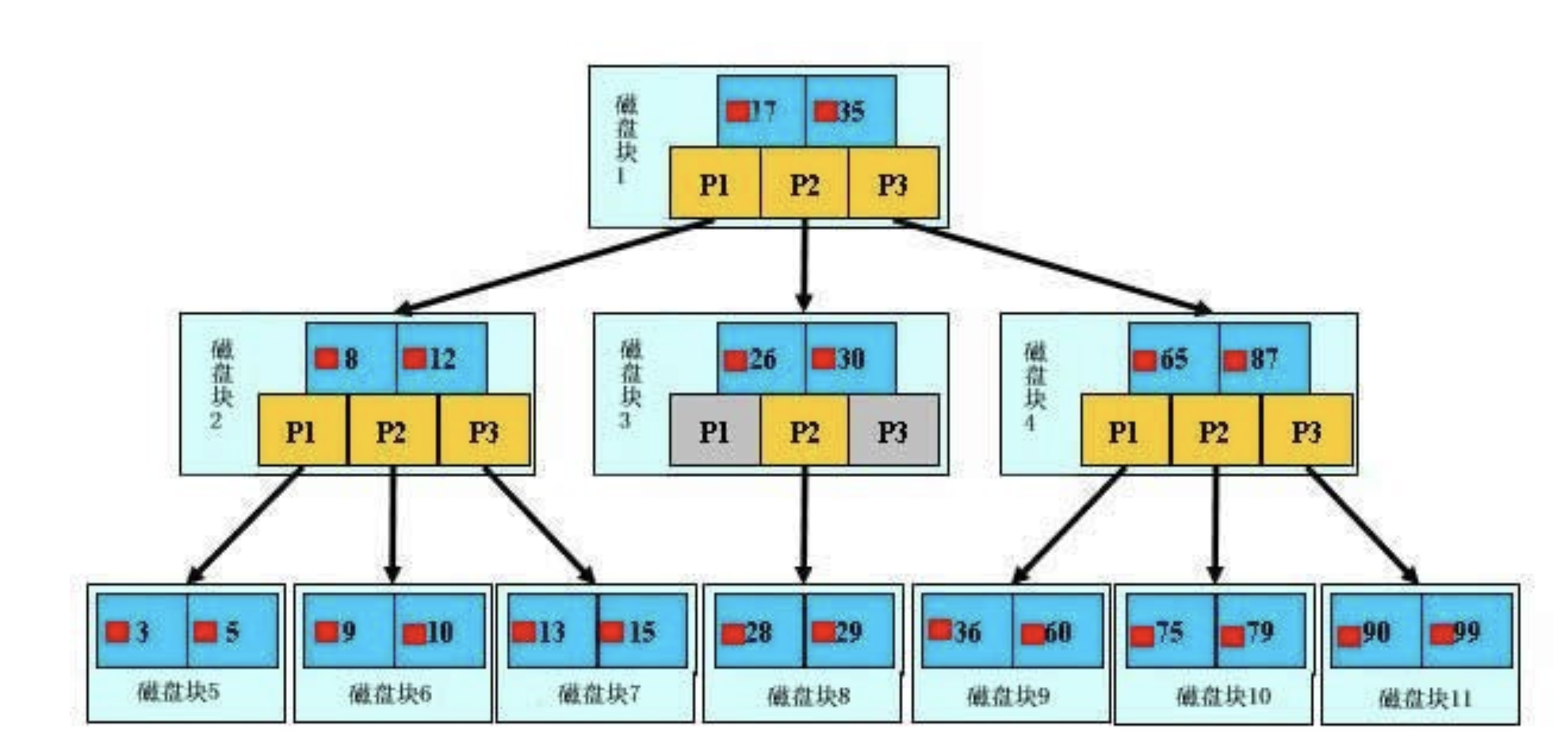
根节点
遵守内部节点拥有孩子的上线,最多有m个。无需遵守下限,因为当树只有根节点时,它没有孩子。
叶子节点
只储存keys和指针,不携带信息:key对应的data是空的。
非叶结点是由叶结点分裂而来的,所以叶结点关键字个数也满足[[m/2]-1,m-1];
B树的插入
插入操作,是插入一条记录,即key:value对儿。从叶子节点插入记录,如果需要从下向上调整。
过程:
1. 插入记录,根据key的值,找到对应的叶子节点。
2.判断当前节点的key的数量是否<= M-1, true则完成插入,false则继续第三步。
3.把当前节点以中间位置的key为中心,左右的key被“分裂”成两个子节点,中间的key上传到父亲节点中。然后将父节点作为“当前节点”,继续2,3步骤。最坏的情况是一直分裂到root节点,建立一个新的root,整个B树增加一层。!
B树的删除
根据key删除记录。
删除方法类似2-3树。看是否是叶子节点。
参考:https://zhuanlan.zhihu.com/p/27700617
- 如果删除的key位于非叶节点,则使用后继key(即中序排列后的后继记录)覆盖要删除的key,然后在叶节点上删除后继key。
- 现在“当前节点”为删除后继key的节点。该节点要key的数量满足[m/2]-1,true则结束删除操作,false则继续下一步。
- 从父兄那里借key来满足B树结构定义。判断兄弟节点是否有富裕的key:
- true则通过兄弟节点上传一个key,再从父亲那下移一个key来完成B树结构,删除操作结束。
- false则看看父亲那里是否有富裕的节点:
- true的话从父亲那借用一个节点,然后再和一个兄弟合并,删除操作结束。
- false的话,仍然从父亲那借用节点并和一个兄弟合并。此时父亲节点不满足[m/2]-1的条件,因此以父节点为“当前节点”,向它的父兄借用节点。即再执行第三步。
举例子:
这是一棵m=5的B树,删除C
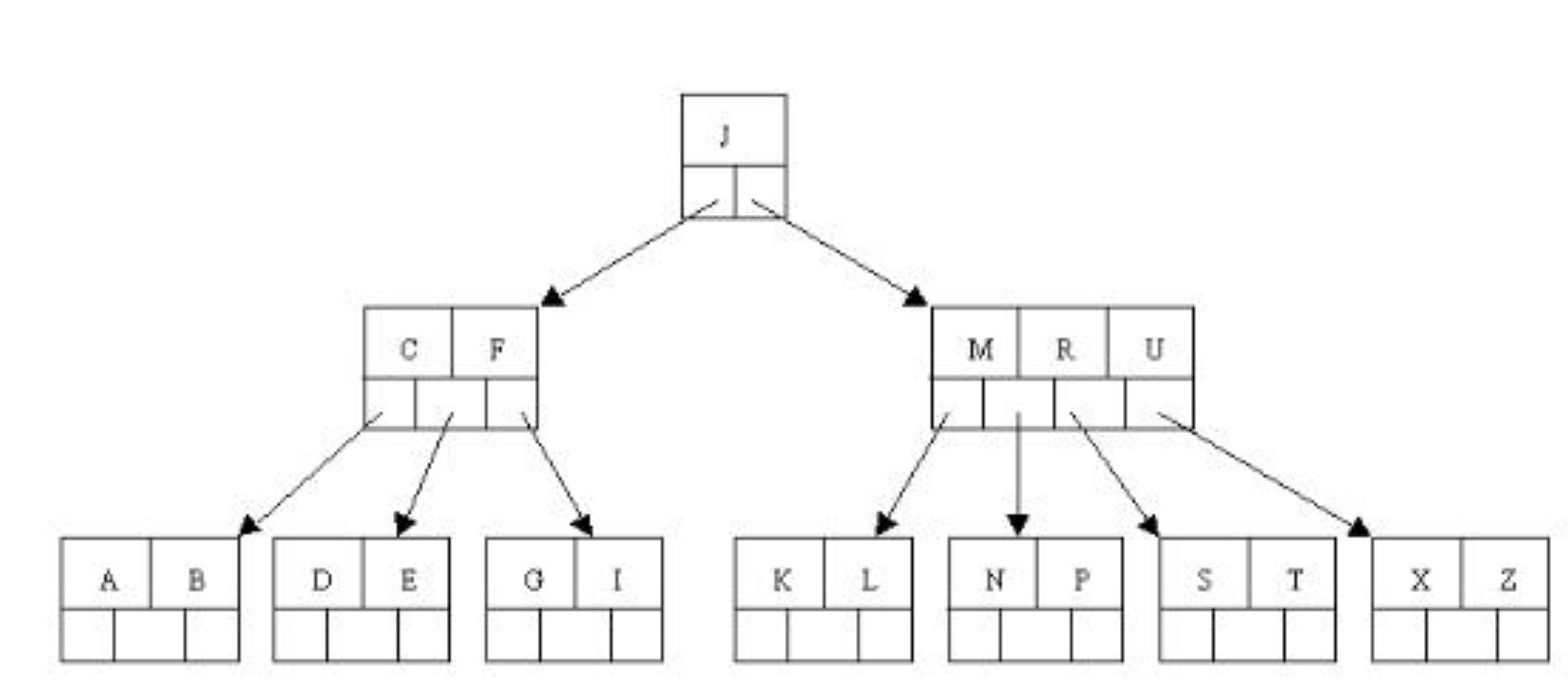
通过上面的步骤可知:
1.找到c的后继D, 然后上移D代替C(代码是复制key,删除原来的D)。
2.发现上移D导致节点不符合定义(最少元素要[m/2]-1), 通过判断父兄都不富裕,所以只能下移D,然后A,B,D,E元素合并为一个节点。
3.此时父节点只有F元素了,所以继续判断,因为它的兄弟节点有富裕元素,所以可以借。把j下移到该节点,然后上移M给父节点。
结果:
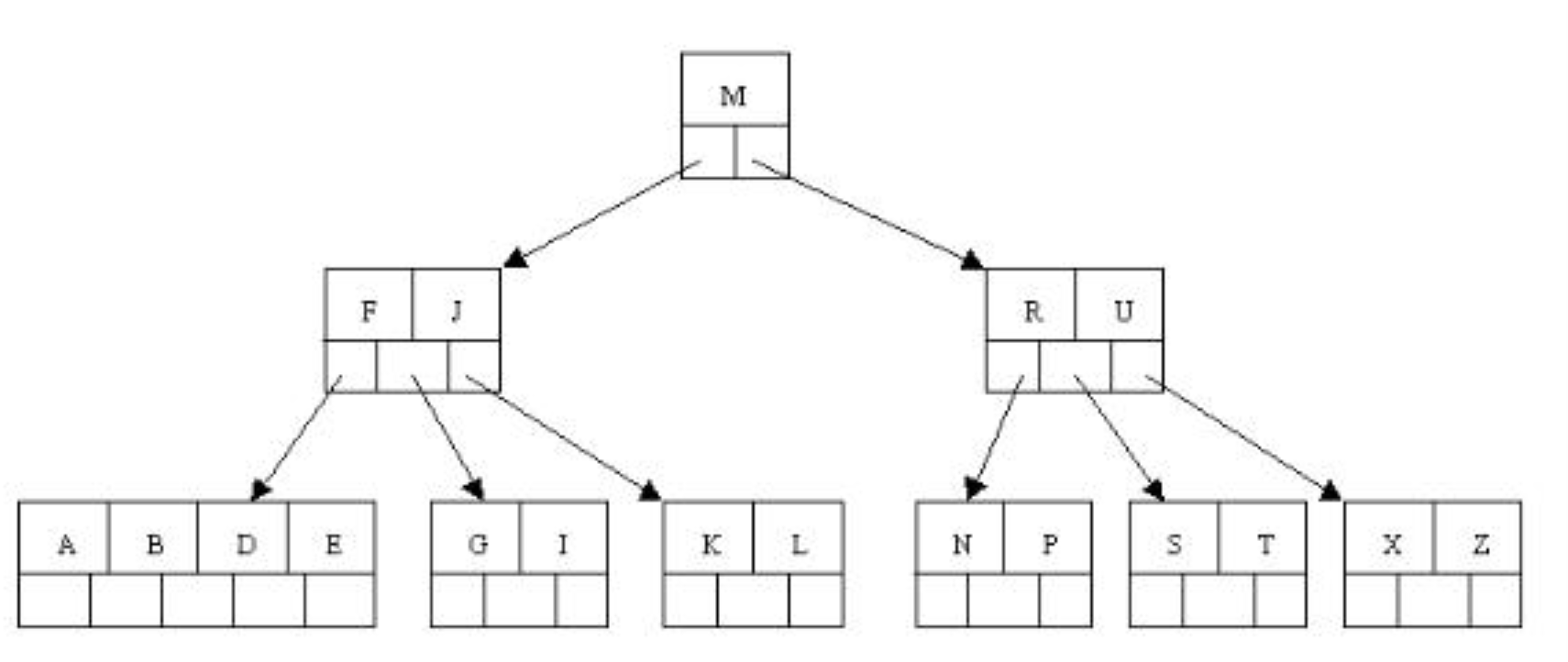
B树的特点:
B树相对于平衡二叉树的不同是,每个节点包含的关键字增多了,特别是在B树应用到数据库中的时候,数据库充分利用了磁盘块的原理(磁盘数据存储是采用块的形式存储的,每个块的大小为4K,每次IO进行数据读取时,同一个磁盘块的数据可以一次性读取出来)把节点大小限制和充分使用在磁盘快大小范围;把树的节点关键字增多后树的层级比原来的二叉树少了,减少数据查找的次数和复杂度;
B+树
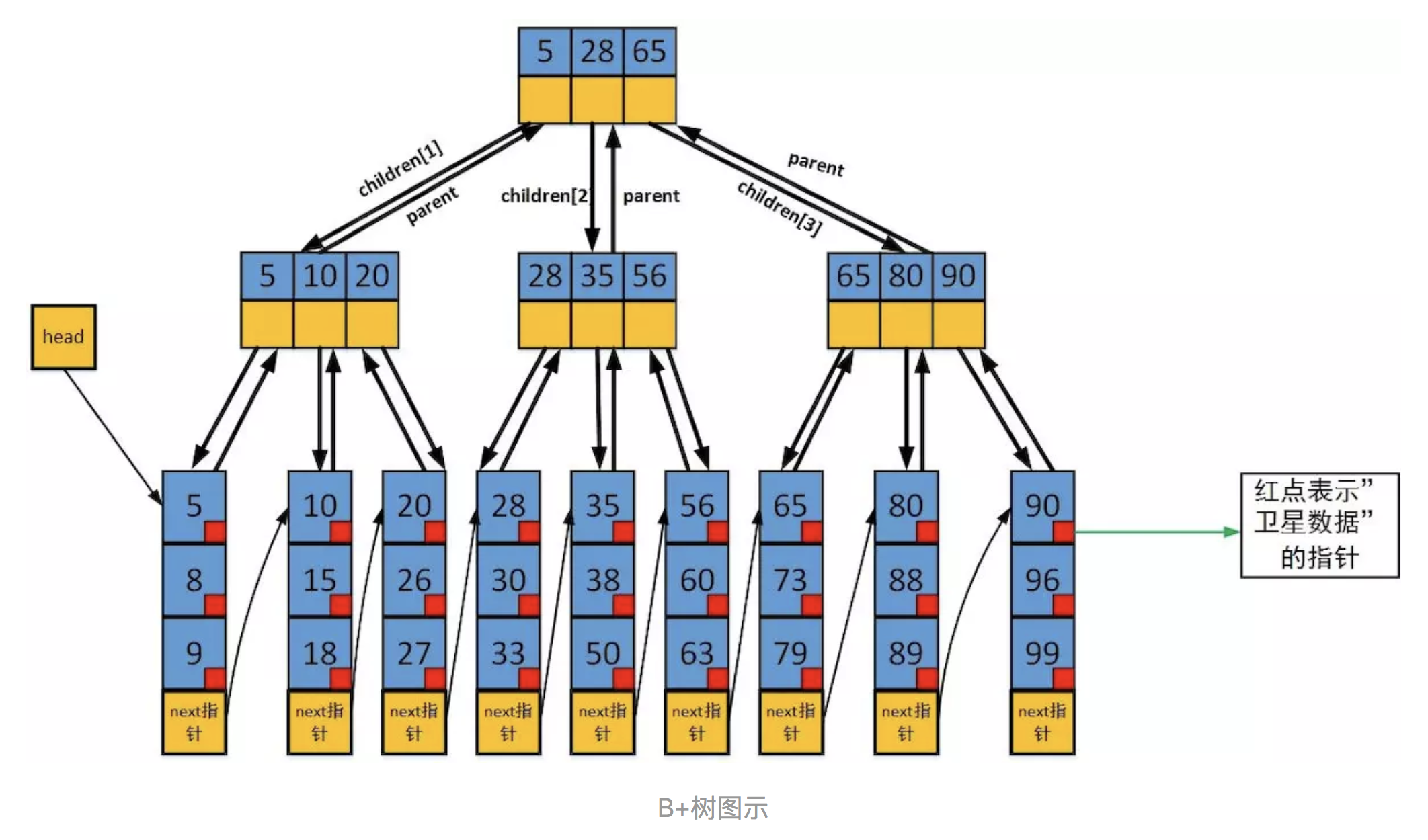
B+树是B树的一个升级版,相对于B树来说B+树更充分的利用了节点的空间,让查询速度更加稳定,其速度完全接近于二分法查找。
传统关系型数据库,主要的索引结构就是B+树。
B+树把所有的数据都储存在叶节点,内部节点只存放关键字和孩子指针。这个特点,让遍历不同于B树。
B树需要使用中序遍历节点,而B+只需把所有的叶子节点串联成链表即可。
- B+树包括2种节点:内部节点(索引节点)和叶子节点。
- 根节点可以是索引节点或叶子节点。根节点的key个数最少可以只有1个
- B+树的内部节点不保存数据,只用于索引,所有的数据/记录保存在叶子节点内。
- m阶B+树:节点最多有m-1个关键字,这和B树一样。
- key按照从小到大的顺序排列。
- 每个叶子节点都保存相邻的叶子节点的pointer。因此方便范围搜索,比B树更快捷。
- ⚠️为了提高效率,规定非叶节点key的数量最低是[m-1]/2。
为什么B+树比B 树更适合实际应用中操作系统的文件索引和数据库索引?
1. B+树的磁盘读写代价更低。
因为内部节点没有指向具体data的指针,因此相对B树更小。如果把所有同一内部结点的关键字存放在同一盘块中,那么盘块所能容纳的关键字数量也越多。一次性读入内存中的需要查找的关键字也就越多。相对来说IO读写次数也就降低了。
2. B树的查询效率更稳定。
只有叶子结点内有具体data的指针,因此任何关键字的查找必须走一条从根结点到叶子结点的路。所有关键字查询的路径长度相同,导致每一个数据的查询效率相当。
3.最重要的是,B+树诞生的目的是解决范围查询的效率问题,它的结构很好解决了这个问题。
B*-tree
B*-tree是B+-tree的变体,在B+树的基础上(所有的叶子结点中包含了全部关键字的信息,及指向含有这些关键字记录的指针),B*树中非根和非叶子结点再增加指向兄弟的指针;B*树定义了非叶子结点关键字个数至少为(2/3)*M,即块的最低使用率为2/3(代替B+树的1/2)。
B+树的分裂:当一个结点满时,分配一个新的结点,并将原结点中1/2的数据复制到新结点,最后在父结点中增加新结点的指针;B+树的分裂只影响原结点和父结点,而不会影响兄弟结点,所以它不需要指向兄弟的指针。
B*树的分裂:当一个结点满时,如果它的下一个兄弟结点未满,那么将一部分数据移到兄弟结点中,再在原结点插入关键字,最后修改父结点中兄弟结点的关键字(因为兄弟结点的关键字范围改变了);如果兄弟也满了,则在原结点与兄弟结点之间增加新结点,并各复制1/3的数据到新结点,最后在父结点增加新结点的指针。
所以,B*树分配新结点的概率比B+树要低,空间使用率更高。
总结:
B树:有序数组+平衡多叉树;
B+树:有序数组链表+平衡多叉树;
B*树:一棵丰满的B+树。
在大规模数据存储的文件系统中,B~tree系列数据结构,起着很重要的作用,对于存储不同的数据,节点相关的信息也是有所不同,
下面是画的一个查找以职工号为关键字key,职工号为38的记录的简单示意图。使用B+树结构储存数据。数据存放在磁盘内。
(这里假设每个物理块容纳3个索引,磁盘的I/O操作的基本单位是块(block), 磁盘访问很费时,采用B+树有效的减少了访问磁盘的次数。)
通过索引节点的搜索,最终在叶节点上找到对应key==38的记录。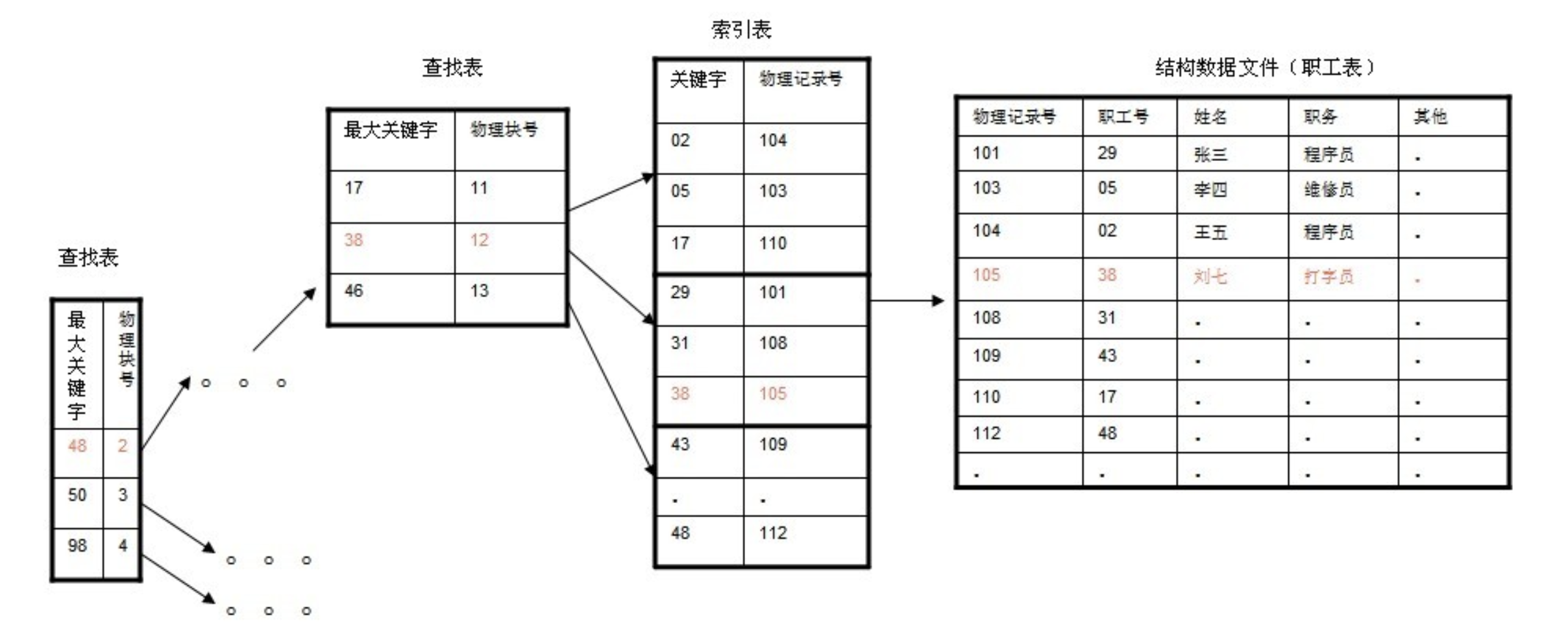
引用:
Bucket Li:"mysql 底层存储是用B+树实现的,知道原因么?内存中B+树是没有优势的,但是一到磁盘,B+树的威力就出来了"。


