DFT计算过程详解
平时工作中,我们在计算傅里叶变换时,通常会直接调用Matlab中的FFT函数,或者是其他编程语言中已经为我们封装好的函数,很少去探究具体的计算过程,本文以一个具体的例子,向你一步一步展示DFT的计算过程。
众所周知,傅里叶变换的计算公式为:
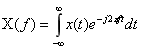
对时域信号进行离散化:

根据欧拉定理:
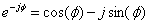
DFT方程改写为:
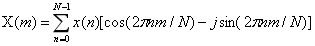
 为第m个DFT输出值,
为第m个DFT输出值,
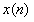 为采样点输入,
为采样点输入,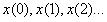
假设N=4:
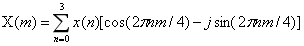
则:
m=0
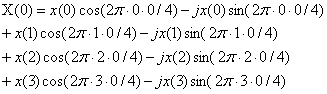
m=1
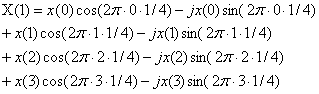
m=2

m=3
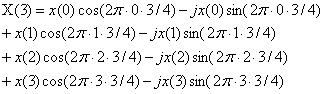
这里需要补充一个采样率的概念。
假设对原始信号的采样率为:
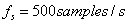
对原始信号做16点DFT进行分析,则基频为:
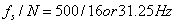
则:
X(0) = 1st frequency term ,with analysis frequency = 0 .31.25 = 0Hz;
X(1) = 2nd frequency term ,with analysis frequency = 1.31.25 = 31.25Hz;
X(2) = 3rd frequency term ,with analysis frequency = 2 .31.25 = 62.5Hz;
X(3) = 4th frequency term ,with analysis frequency = 3 .31.25 = 93.75Hz;
分析频率的公式可以计为:
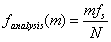
下面进入正题,对一个特定信号进行DFT分析。
原始信号为:

可以看出此信号包含1kHz和2kHz的信号,现在一步一步的对此信号做8点DFT分析。
假设采样率为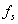 ,即每
,即每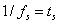 秒采集一个点,由于N=8,因此我们需要8个输入采样点来计算DFT,即对原始信号进行离散化为:
秒采集一个点,由于N=8,因此我们需要8个输入采样点来计算DFT,即对原始信号进行离散化为:

如果采样率samples/s,则DFT的结果将计算的是输入信号x(n)在分析频率,0KHz,1kHz,2KHz,...,7kHz处的梯度值。
则:

当m=1时,即计算原始信号在1kHz下的梯度值:
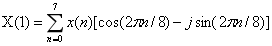

当m=2时,即计算原始信号在2kHz下的梯度值:

当m=3时,即计算原始信号在3kHz下的梯度值:

当m=4时,即计算原始信号在4kHz下的梯度值:

当m=5时,即计算原始信号在5kHz下的梯度值:

当m=6时,即计算原始信号在6kHz下的梯度值:

当m=7时,即计算原始信号在7kHz下的梯度值:

即8个梯度值计算完成:
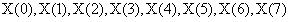



 浙公网安备 33010602011771号
浙公网安备 33010602011771号