递归的浅析与实现
一、定义
若一个对象部分的包含它自己,或用自己来定义自己,则称为这个对象是递归的。
二、应用原则
1、基本条件:递归过程必须一直存在至少一个不使用递归方法解决的条件。
2、进行方向:任何递归调用都必须向着“基本条件”的方向进行。
3、正确假设:总是假设递归调用时有效的。
4、适度原则:避免使用过多的递归,尤其是效率要求高而递归调用链过长的情况下。
5、顺序问题:变动递归调用的顺序有可能导致整个函数执行顺序的变化。
三、用例
1、汉诺塔问题

1 #include <iostream> 2 using namespace std; 3 #define numOfDisks 3 4 //1、汉诺塔问题-递归法 5 void Move(int n, char x, char y) 6 { 7 cout << "move " << n << " from " << x << " to " << y<<endl; 8 } 9 10 void Hannoi(int n,char a,char b,char c) 11 { 12 if (n == 1) 13 { 14 Move(n, a, c); 15 } 16 else 17 { 18 Hannoi(n - 1, a, c, b); 19 Move(n, a, c); 20 Hannoi(n - 1, b, a, c); 21 } 22 } 23 int main() 24 { 25 Hannoi(numOfDisks, 'a', 'b', 'c'); 26 system("pause"); 27 return 0; 28 }
测试结果:
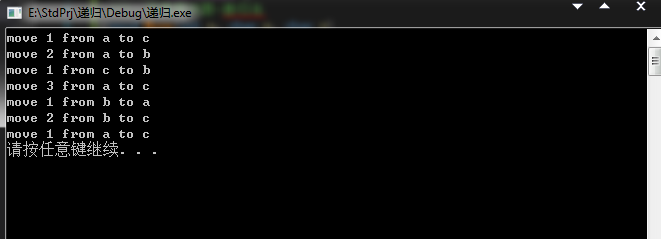
2、八皇后问题

1 #include <iostream> 2 #define MAX 4 3 int sum = 0; 4 using namespace std; 5 //2、八皇后问题-回溯法 6 //首先要皇后不冲突,则每行只能有一个皇后 7 //用queens[]数组来表示每个皇后存储的位置,如queens[m] = n 表示第m行的皇后放在第n列上 8 class QueenPuzzle 9 { 10 public: 11 void printOut(); //打印结果 12 bool IsValid(int n); //判断第n个皇后放上去是否合适 13 void placeQueen(int n); //递归算法放置皇后 14 15 16 private: 17 int queens[MAX]; 18 }; 19 20 void QueenPuzzle::printOut() 21 { 22 for (int i =0;i<MAX;i++) 23 { 24 for (int j=0;j<MAX;j++) 25 { 26 if (j==queens[i]) 27 cout << "X "; 28 else 29 cout << "0 "; 30 } 31 cout << endl; 32 } 33 } 34 35 36 bool QueenPuzzle::IsValid(int n) 37 { 38 //将第n个皇后的位置依次和前面的 39 for (int i = 0; i < n; i++) 40 { 41 //两个皇后在同一列上,返回false 42 if (queens[i] == queens[n]) 43 return false; 44 //两个皇后在同一对角线上,返回false 45 if (abs(queens[i] - queens[n]) == n - i) 46 return false; 47 } 48 return true; 49 } 50 51 void QueenPuzzle::placeQueen(int n) 52 { 53 for (int i =0;i<MAX;i++) 54 { 55 if (n==MAX) //如果放完了,则直接输出结果 56 { 57 sum++; 58 cout << "第" << sum << "组解:" << endl; 59 printOut(); 60 return; 61 } 62 //放置后 63 queens[n] = i; 64 //次位置内不能放置皇后 65 if (IsValid(n)) 66 placeQueen(n + 1); 67 } 68 } 69 70 int main() 71 { 72 QueenPuzzle queen; 73 queen.placeQueen(0); 74 cout << "共" << sum << "组解"; 75 system("pause"); 76 return 0; 77 }
测试结果:(测试中用的是四皇后)

海阔凭鱼跃,天高任鸟飞。




