树的浅析与实现

一、基本概念

　　树是一种简单的非线性结构，所有元素之间具有明显的层次特性。在树结构中，每一个结点只有一个前驱节点，称为父结点，没有前驱节点的结点只有一个，称为树的根结点，简称树的根。每一个结点可以有多个后继节点，称为该结点的子结点。没有后继节点的结点称为叶子结点。在树结构中，一个结点所拥有的后件的个数称为该结点的度，所有结点中最大的度称为树的度。树的最大层次称为树的深度。

二、二叉树

　　定义：二叉树是每个结点最多有两个子树的树结构。通常子树被称作“左子树”（left subtree）和“右子树”（right subtree）。二叉树常被用于实现二叉查找树和二叉堆。二叉树通常分为满二叉树和完全二叉树。

　　（1）满二叉树：一个深度为K且有2^k+1-1个节点的二叉树。

　　（2）完全二叉树：只多有最下面的两层的节点的度数可以小于2，其余各层节点的度数都等于2，并且最下面一层的节点都集中在该层最左边的若干位置。

　　性质：

　　（1）对于非空二叉树，其i层最大的节点数目为2ⁱ，其中i>=0。

　　（2）深度为k的二叉树之多有2^k+1-1个节点，其中k>=-1。

　　（3）在任意一棵非空二叉树中，若终端节点的个数为n_0，度为2的节点数为n₂，则存在n₀ = n₂ +1。

　　（4）具有n个节点的完全二叉树的深度为k等于log₂(n+1)向上取整再减1。

　　（5）如将一棵有n个节点的完全二叉树子上（根节点）向下（叶节点），同一层，子做向右连续赋予节点编号0,1,2,3,4....，n-1则对任意下标为i的节点有：

　　　　1、若i=0，则i为根节点，无父节点；若i>0,i>0，则i的父节点下标为（i-1）/2向下取整。

　　　　2、若2*i+1<n,则i的左子女为2*i+1。

　　　　3、若2*i+2<n,则i的右子女为2*i+2。

　　　　4、若i为偶数，且i≠0，则左兄弟为i-1。

　　　　5、若i为奇数，且i≠n-1，则右兄弟为i+1。

　　　　6、节点i所在的层次为log₂(i+1)向下取整。

　　实现：

树节点定义

 1 #pragma once
 2 #include <iostream>  
 3 #include <assert.h>  
 4 using namespace std;
 5 template <class T>
 6 class BinaryTreeNode
 7 {
 8 public:
 9     BinaryTreeNode();
10     BinaryTreeNode(BinaryTreeNode* node);
11     void setData(const T &value);                        //设置节点值
12     void setParent(BinaryTreeNode<T>*parent);            //设置父节点
13     void setLeftChild(BinaryTreeNode<T>*leftchild);        //设置左孩子节点
14     void setRightChild(BinaryTreeNode<T>*rightchild);    //设置右孩子节点
15     T& getData();                                        //获取节点值
16     BinaryTreeNode<T>* getparent();                        //获取父节点
17     BinaryTreeNode<T>* getLeftChild();                    //获取左孩子节点
18     BinaryTreeNode<T>* getRightChild();                    //获取右孩子节点
19 
20 private:
21     T m_value;                               //存储值
22     BinaryTreeNode<T>* m_parent;             //指向父节点
23     BinaryTreeNode<T>* m_leftChilde;         //指向左孩子节点
24     BinaryTreeNode<T>* m_rightChilde;         //指向右孩子节点
25 };
26 
27 
28 
29 
30 template <class T>
31 BinaryTreeNode<T>::BinaryTreeNode()
32 {
33     m_parent = NULL;
34     m_leftChilde = NULL;
35     m_rightChilde = NULL;
36 }
37 
38 template <class T>
39 BinaryTreeNode<T>::BinaryTreeNode(BinaryTreeNode* node)
40 {
41     m_value = node->getData();
42     m_parent = node->getparent();
43     m_leftChilde = node->getLeftChild();
44     m_rightChilde = node->getRightChild();
45 }
46  
47 template <class T>
48 void BinaryTreeNode<T>::setData(const T &value)
49 {
50     m_value = value;
51 }
52 
53 template <class T>
54 void BinaryTreeNode<T>::setParent(BinaryTreeNode<T>*parent)
55 {
56     m_parent = parent;
57 }
58 
59 template <class T>
60 void BinaryTreeNode<T>::setRightChild(BinaryTreeNode<T>*rightchild)
61 {
62     m_rightChilde = rightchild;
63 }
64 
65 template <class T>
66 void BinaryTreeNode<T>::setLeftChild(BinaryTreeNode<T>*leftchild)
67 {
68     m_leftChilde = leftchild;
69 }
70 
71 template <class T>
72 T& BinaryTreeNode<T>::getData()
73 {
74     return m_value;
75 }
76 
77 template <class T>
78 BinaryTreeNode<T>* BinaryTreeNode<T>::getparent()
79 {
80     return m_parent;
81 }
82 
83 template <class T>
84 BinaryTreeNode<T>* BinaryTreeNode<T>::getRightChild()
85 {
86     return m_rightChilde;
87 }
88 
89 template <class T>
90 BinaryTreeNode<T>* BinaryTreeNode<T>::getLeftChild()
91 {
92     return m_leftChilde;
93 }

binaryTreeNode.h

树定义

  1 #pragma once
  2 #include <iostream>  
  3 #include <assert.h> 
  4 #include <stack>
  5 #include <queue>
  6 #include "binaryTreeNode.h"
  7 using namespace std;
  8 template <class T>
  9 class BinaryTree
 10 {
 11 public:
 12     BinaryTree(T &value);
 13     BinaryTree(BinaryTreeNode<T>* node);
 14     BinaryTreeNode<T>* getRoot();   //获取根节点
 15     void insertLeftChild(BinaryTreeNode<T>* root, T &value);  //插入左孩节点
 16     void insertRightChild(BinaryTreeNode<T>* root,T &value);  //插入右孩子节点
 17     bool isEmpty(); //判断是否为空
 18     //树的遍历
 19     //前序遍历
 20     void preOrderTraverse1(BinaryTreeNode<T>* root) const; //使用递归实现
 21     void preOrderTraverse2(BinaryTreeNode<T>* root) const; //使用栈结构实现
 22     //中序遍历
 23     void inOrderTraverse1(BinaryTreeNode<T>* root) const; //使用递归实现
 24     void inOrderTraverse2(BinaryTreeNode<T>* root) const; //使用栈结构实现
 25     //后序遍历
 26     void postOrderTraverse1(BinaryTreeNode<T>* root) const; //使用递归实现
 27     void postOrderTraverse2(BinaryTreeNode<T>* root) const; //使用栈结构实现
 28     //层序遍历
 29     void levelOrderTraverse(BinaryTreeNode<T>* root) const;
 30 private:
 31     BinaryTreeNode<T>* m_root;  //根节点
 32 };
 33 
 34 
 35 
 36 
 37 
 38 //构造函数
 39 template <class T>
 40 BinaryTree<T>::BinaryTree(T &value)
 41 {
 42     m_root = new BinaryTreeNode<T>();
 43     m_root->setData(value);
 44 }
 45 
 46 template <class T>
 47 BinaryTree<T>::BinaryTree(BinaryTreeNode<T>* node)
 48 {
 49     m_root = new BinaryTreeNode<T>(); //创建一个新的节点
 50     m_root = node;
 51 }
 52 
 53 //设置子节点函数
 54 template <class T>
 55 void BinaryTree<T>::insertRightChild(BinaryTreeNode<T>* root, T &value)
 56 {
 57     BinaryTreeNode<T>* childNode = new BinaryTreeNode<T>();
 58     childNode->setData(value);
 59     childNode->setParent(root);
 60     root->setRightChild(childNode);
 61 }
 62 
 63 template <class T>
 64 void BinaryTree<T>::insertLeftChild(BinaryTreeNode<T>* root, T &value)
 65 {
 66     BinaryTreeNode<T>* childNode = new BinaryTreeNode<T>();
 67     childNode->setData(value);
 68     childNode->setParent(root);
 69     root->setLeftChild(childNode);
 70 }
 71 
 72 //获取根节点函数
 73 template <class T>
 74 BinaryTreeNode<T>* BinaryTree<T>::getRoot()
 75 {
 76     return m_root;
 77 }
 78 
 79 template <class T>
 80 bool BinaryTree<T>::isEmpty()
 81 {
 82     return m_root->getparent();
 83 }
 84 
 85 //遍历函数
 86 //1、前序遍历
 87 template <class T>
 88 void BinaryTree<T>::preOrderTraverse1(BinaryTreeNode<T>* root) const
 89 {
 90     if (NULL !=root)
 91     {
 92         cout << root->getData() << "->";
 93         preOrderTraverse1(root->getLeftChild());
 94         preOrderTraverse1(root->getRightChild());
 95     }
 96 }
 97 
 98 template <class T>
 99 void BinaryTree<T>::preOrderTraverse2(BinaryTreeNode<T>* root) const
100 {
101     stack<BinaryTreeNode<T>*> s;
102     BinaryTreeNode<T>* p = root;
103     while (!s.empty() || p!=NULL)
104     {
105         while (p)
106         {
107             s.push(p);
108             cout << p->getData() << "->";
109             p = p->getLeftChild();
110         }
111         p = s.top();
112         s.pop();
113         p = p->getRightChild();
114 
115     }
116 }
117 
118 //2、中序遍历
119 template <class T>
120 void BinaryTree<T>::inOrderTraverse1(BinaryTreeNode<T>* root) const
121 {
122     if (NULL != root)
123     {
124         inOrderTraverse1(root->getLeftChild());
125         cout << root->getData() << "->";
126         inOrderTraverse1(root->getRightChild());
127     }
128 }
129 
130 template <class T>
131 void BinaryTree<T>::inOrderTraverse2(BinaryTreeNode<T>* root) const
132 {
133     stack<BinaryTreeNode<T>*> s;
134     BinaryTreeNode<T>*p = root;
135     while (!s.empty() || p != NULL)
136     {
137         while (p)
138         {
139             s.push(p);
140             p = p->getLeftChild();
141         }
142         p = s.top();
143         s.pop();
144         cout << p->getData()<<"->";
145         p = p->getRightChild();
146     }
147 }
148 
149 //2、后序遍历
150 template <class T>
151 void BinaryTree<T>::postOrderTraverse1(BinaryTreeNode<T>* root) const
152 {
153     if (NULL!=root)
154     {
155         postOrderTraverse1(root->getLeftChild());
156         postOrderTraverse1(root->getRightChild());
157         cout << root->getData() << "->";
158     }
159 }
160 
161 template <class T>
162 void BinaryTree<T>::postOrderTraverse2(BinaryTreeNode<T>* root) const
163 {
164     stack<BinaryTreeNode<T>*> s;
165     BinaryTreeNode<T> *cur;            //当前节点
166     BinaryTreeNode<T> *pre = NULL;  //上一次访问的节点
167     s.push(root);
168     while (!s.empty() )
169     {
170         cur = s.top();
171         if ((cur->getLeftChild() == NULL) && (cur->getRightChild() == NULL)
172             || (pre != NULL)&&(pre ==cur->getLeftChild()||pre==cur->getRightChild()))
173         {
174             cout << cur->getData() << "->"; //如果当前结点没有孩子结点或者孩子节点都已被访问过 
175             s.pop();
176             pre = cur;
177         }
178         else
179         {
180             if (cur->getRightChild() != NULL)
181             {
182                 s.push(cur->getRightChild());
183             }
184             if (cur->getLeftChild() != NULL)
185             {
186                 s.push(cur->getLeftChild());
187             }
188         }
189 
190     }
191 
192 
193 }
194 //层序遍历
195 template <class T>
196 void BinaryTree<T>::levelOrderTraverse(BinaryTreeNode<T>* root) const
197 {
198     queue<BinaryTreeNode<T>* > q;
199     BinaryTreeNode<T>* p;
200     q.push(root);
201         while (!q.empty())
202         {
203             p = q.front();
204             if (p->getLeftChild() != NULL)
205                 q.push(p->getLeftChild());
206             if (p->getRightChild() != NULL)
207                 q.push(p->getRightChild());
208             q.pop();
209             cout << p->getData() << "->";
210     }
211 }

BinaryTree.h

测试代码

 1 #include <stdio.h>
 2 #include <iostream>
 3 #include "BinaryTree.h"
 4 #include "binaryTreeNode.h"
 5 using namespace std;
 6 int main()
 7 {
 8     char value = 'A';
 9     BinaryTree<char> mytree(value);
10     value++;
11     mytree.insertLeftChild(mytree.getRoot(), value);
12     value++;
13     mytree.insertRightChild(mytree.getRoot(), value);
14     value++;
15     mytree.insertLeftChild(mytree.getRoot()->getLeftChild(), value);
16     value++;
17     mytree.insertRightChild(mytree.getRoot()->getLeftChild(), value);
18     value++;
19     mytree.insertLeftChild(mytree.getRoot()->getRightChild(), value);
20     value++;
21     mytree.insertRightChild(mytree.getRoot()->getRightChild(), value);
22  
23     cout << mytree.getRoot()->getData() << "\n";
24     cout << mytree.getRoot()->getLeftChild()->getData() << "\n";
25     cout << mytree.getRoot()->getRightChild()->getData() << "\n";
26     cout << mytree.getRoot()->getLeftChild()->getLeftChild()->getData() << "\n";
27     cout << mytree.getRoot()->getLeftChild()->getRightChild()->getData() << "\n";
28     cout << mytree.getRoot()->getRightChild()->getLeftChild()->getData() << "\n";
29     cout << mytree.getRoot()->getRightChild()->getRightChild()->getData() << "\n";
30     cout <<"前序遍历递归实现"<<endl;
31     mytree.preOrderTraverse1(mytree.getRoot());
32     cout << endl;
33     cout << "前序遍历栈实现" << endl;
34     mytree.preOrderTraverse2(mytree.getRoot());
35     cout << endl;
36     cout << "中序遍历递归实现" << endl;
37     mytree.inOrderTraverse1(mytree.getRoot());
38     cout << endl;
39     cout << "中序遍历栈实现" << endl;
40     mytree.inOrderTraverse2(mytree.getRoot());
41     cout << endl;
42     cout << "后序遍历递归实现" << endl;
43     mytree.postOrderTraverse1(mytree.getRoot());
44     cout << endl;
45     cout << "后序遍历栈实现" << endl;
46     mytree.postOrderTraverse2(mytree.getRoot());
47     cout << endl;
48     cout << "层序遍历实现" << endl;
49     mytree.levelOrderTraverse(mytree.getRoot());
50     
51     
52     return 0;
53 }

测试代码

测试结果

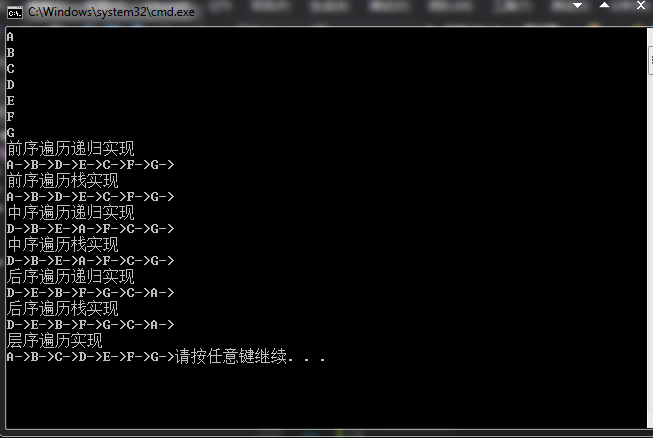
三、任意树

　　定义：任意树，只有一个根节点，但有任意个子节点。树的存储方式有多种方式，常用的有双亲节点数组表示法、孩子节点多重链表表示法、孩子节点链表表示法、左子女-右兄弟表示法。

例：任意树如下

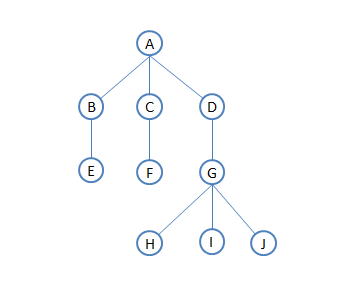
双亲节点数组表示法：

孩子节点多重链表表示法：

左子女-右兄弟表示法：

实现：

　　如下代码采用左孩子-右兄弟的方法实现。

树节点定义

 1 #pragma once
 2 template<class T>
 3 class TreeNode
 4 {
 5 public:
 6     TreeNode(const T&);                                //构造函数
 7     ~TreeNode();
 8     bool isLeft();                                    //是否为叶子节点
 9     T getValue();                                    //获取当前节点值
10     TreeNode<T> *getLeftChild();                    //获取该节点的最左子节点
11     TreeNode<T> *getRightSibling();                    //获取该节点的最右兄弟节点
12     void setValue(T &value);                        //设置当前节点值
13     void setLeftChild(TreeNode<T> * pLeftChild);    //设置该节点的最左子节点
14     void setRightSibling(TreeNode<T> *pRightSibling);//设置该节点的最右兄弟节点
15 private:
16     T m_value;
17     TreeNode<T> *leftChild;
18     TreeNode<T> *rightSibling;
19 
20 };
21 
22 template<class T>
23 TreeNode<T>::TreeNode(const T& value)
24 {
25     m_value = value;
26     leftChild = rightSibling = NULL;
27 }
28 
29 template<class T>
30 TreeNode<T>::~TreeNode()
31 {
32 
33 }
34 
35 template<class T>
36 bool TreeNode<T>::isLeft()
37 {
38     if (NULL == leftChild)
39         return true;
40     else
41         return false;
42 }
43 
44 template<class T>
45 TreeNode<T> * TreeNode<T>::getRightSibling()
46 {
47     return rightSibling;
48 }
49 
50 template<class T>
51 TreeNode<T> * TreeNode<T>::getLeftChild()
52 {
53     return leftChild;
54 }
55 
56 template<class T>
57 T TreeNode<T>::getValue()
58 {
59     return m_value;
60 }
61 
62 template<class T>
63 void TreeNode<T>::setRightSibling(TreeNode<T> *pRightSibling)
64 {
65     rightSibling = pRightSibling;
66 }
67 
68 template<class T>
69 void TreeNode<T>::setLeftChild(TreeNode<T> * pLeftChild)
70 {
71     leftChild = pLeftChild;
72 }
73 
74 template<class T>
75 void TreeNode<T>::setValue(T &value)
76 {
77     m_value = value;
78 }

treeNode.h

树定义

  1 #pragma once
  2 #include <queue>
  3 #include "treeNode.h"
  4 
  5 template<class T>
  6 class Tree
  7 {
  8 public:
  9     Tree();
 10     Tree(TreeNode<T>* rt);
 11     ~Tree();
 12     //获取该树的根节点
 13     TreeNode<T>* getRoot(); 
 14     //获取节点current的父节点
 15     TreeNode<T>* Parent(TreeNode<T>* current);
 16     //获取节点t的第一个子节点，若无则返回NULL
 17     TreeNode<T>* getFirstChild(TreeNode<T>* t); 
 18     //获取节点t的下一个兄弟节点，若无则返回NULL
 19     TreeNode<T>* getNextSibling(TreeNode<T>* t);
 20     //在t节点插入一个子节点n
 21     void insertChild(TreeNode<T>* t, TreeNode<T>* n);
 22     //删除以t为根节点的子树
 23     void deleteSubTree(TreeNode<T>* t);
 24     //判断是否为空树
 25     bool isEmpty();
 26     //遍历树
 27     void OrderTraverse();
 28 
 29 private:
 30     TreeNode<T> *root, *parent;
 31     int getParent(TreeNode<T>* root,TreeNode<T>* current);
 32 };
 33 
 34 
 35 
 36 template<class T>
 37 Tree<T>::Tree()
 38 {
 39     root = parent = NULL;
 40 }
 41 
 42 template<class T>
 43 Tree<T>::Tree(TreeNode<T>* rt)
 44 {
 45     root = rt;
 46     parent = NULL;
 47 }
 48 
 49 template<class T>
 50 Tree<T>::~Tree()
 51 {
 52 
 53 }
 54 
 55 template<class T>
 56 TreeNode<T>* Tree<T>::getRoot()
 57 {
 58     return root;
 59 }
 60 
 61 template<class T>
 62 TreeNode<T>* Tree<T>::Parent(TreeNode<T>* current)
 63 {
 64     TreeNode<T> * pointer = current;
 65     TreeNode<T> *t;
 66 
 67     if (current == NULL || current == root)
 68     {
 69         return NULL;
 70     }
 71     t = root;
 72     getParent(t, pointer);
 73     return parent;
 74 }
 75 
 76 template<class T>
 77 TreeNode<T>* Tree<T>::getFirstChild(TreeNode<T>* t)
 78 {
 79     return t->getLeftChild();
 80 }
 81 
 82 template<class T>
 83 TreeNode<T>* Tree<T>::getNextSibling(TreeNode<T>* t)
 84 {
 85     return t->getRightSibling();
 86 }
 87 
 88 template<class T>
 89 void Tree<T>::insertChild(TreeNode<T>* t, TreeNode<T>* n)
 90 {
 91     if (t->getLeftChild() == NULL)
 92         t->setLeftChild(n);
 93     else
 94     {
 95         TreeNode<T>* p = t->getLeftChild();
 96         while (p->getRightSibling() != NULL)
 97             p = p->getRightSibling();
 98         p->setRightSibling(n);
 99     }
100 }
101 
102 template<class T>
103 void Tree<T>::deleteSubTree(TreeNode<T>* t)
104 {
105     if (t == root)
106     {
107         root = NULL;
108     }
109     else
110     {
111         TreeNode<T>* p = Parent(t);
112         TreeNode<T>* q = p->getLeftChild();
113         if (q == t)
114         {
115             p->setLeftChild(t->getRightSibling());
116         }
117         else
118         {
119             while (q != t)
120             {
121                 p = q;
122                 q = q->getRightSibling();
123             }
124             p->setRightSibling(q->getRightSibling());    
125         }
126     }
127 }
128 
129 template<class T>
130 int Tree<T>::getParent(TreeNode<T>* root, TreeNode<T>* current)
131 {
132     //深度优先的遍历找到current 节点
133     TreeNode<T>* q = root->getLeftChild();
134     while (q!=NULL && q!=current)
135     {
136         if (getParent(q, current) != 0)
137             return 2;
138         q = q->getRightSibling();
139     }
140 
141     if (q!=NULL && q==current)
142     {
143         parent = root;
144         return 1;
145     }
146     else
147     {
148         return 0;
149     }
150 
151 }
152 
153 template<class T>
154 bool Tree<T>::isEmpty()
155 {
156     if (NULL == root)
157         return true;
158     else
159         return false;
160 }
161 
162 template<class T>
163 void Tree<T>::OrderTraverse()
164 {
165     queue<TreeNode<T>*> q;
166     TreeNode<T>* p;
167     q.push(root);
168     while (!q.empty())
169     {
170         p = q.front();
171         if (p->getRightSibling()!=NULL)
172         {
173             q.push(p->getRightSibling());
174         }
175         if (p->getLeftChild() != NULL)
176         {
177             q.push(p->getLeftChild());
178         }
179         q.pop();
180         cout << p->getValue() << "->";
181 
182     }
183 }

tree.h

测试代码

 1 #include <stdio.h>
 2 #include <iostream>
 3 #include "treeNode.h"
 4 #include "tree.h"
 5 using namespace std;
 6 int main()
 7 {
 8     char value = 'A';
 9     //构建一个树
10     TreeNode<char> *rootNode = new TreeNode<char>(value);
11     Tree<char> mytree(rootNode);
12     value++;
13     TreeNode<char> *node_B = new TreeNode<char>(value);
14     mytree.insertChild(rootNode, node_B);
15     value++;
16     TreeNode<char> *node_C = new TreeNode<char>(value);
17     mytree.insertChild(rootNode, node_C);
18     value++;
19     TreeNode<char> *node_D = new TreeNode<char>(value);
20     mytree.insertChild(rootNode, node_D);
21 
22 
23     value++;
24     TreeNode<char> *node_E = new TreeNode<char>(value);
25     mytree.insertChild(node_B, node_E);
26     value++;
27     TreeNode<char> *node_F = new TreeNode<char>(value);
28     mytree.insertChild(node_C, node_F);
29     value++;
30     TreeNode<char> *node_G = new TreeNode<char>(value);
31     mytree.insertChild(node_D, node_G);
32 
33 
34     value++;
35     TreeNode<char> *node_H = new TreeNode<char>(value);
36     mytree.insertChild(node_G, node_H);
37     value++;
38     TreeNode<char> *node_I = new TreeNode<char>(value);
39     mytree.insertChild(node_G, node_I);
40     value++;
41     TreeNode<char> *node_J = new TreeNode<char>(value);
42     mytree.insertChild(node_G, node_J);
43     //2、遍历一下树
44     cout << "遍历树" << endl;
45     mytree.OrderTraverse();
46     cout << endl;
47 
48     cout << "获取节点C的父节点" << endl;
49     cout << mytree.Parent(node_C)->getValue();
50     cout << endl;
51     cout << "删除节点F" << endl;
52     mytree.deleteSubTree(node_F);
53     mytree.OrderTraverse();
54     cout << endl;
55 
56 
57     system("pause");
58     return 0;
59 }

test.cpp

测试结果

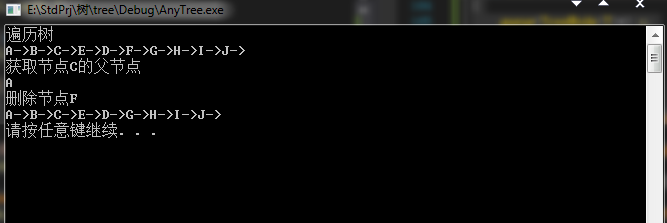
 1 #pragma once
 2 template<class T>
 3 class TreeNode
 4 {
 5 public:
 6     TreeNode(const T&);                                //构造函数
 7     ~TreeNode();
 8     bool isLeft();                                    //是否为叶子节点
 9     T getValue();                                    //获取当前节点值
10     TreeNode<T> *getLeftChild();                    //获取该节点的最左子节点
11     TreeNode<T> *getRightSibling();                    //获取该节点的最右兄弟节点
12     void setValue(T &value);                        //设置当前节点值
13     void setLeftChild(TreeNode<T> * pLeftChild);    //设置该节点的最左子节点
14     void setRightSibling(TreeNode<T> *pRightSibling);//设置该节点的最右兄弟节点
15 private:
16     T m_value;
17     TreeNode<T> *leftChild;
18     TreeNode<T> *rightSibling;
19 
20 };
21 
22 template<class T>
23 TreeNode<T>::TreeNode(const T& value)
24 {
25     m_value = value;
26     leftChild = rightSibling = NULL;
27 }
28 
29 template<class T>
30 TreeNode<T>::~TreeNode()
31 {
32 
33 }
34 
35 template<class T>
36 bool TreeNode<T>::isLeft()
37 {
38     if (NULL == leftChild)
39         return true;
40     else
41         return false;
42 }
43 
44 template<class T>
45 TreeNode<T> * TreeNode<T>::getRightSibling()
46 {
47     return rightSibling;
48 }
49 
50 template<class T>
51 TreeNode<T> * TreeNode<T>::getLeftChild()
52 {
53     return leftChild;
54 }
55 
56 template<class T>
57 T TreeNode<T>::getValue()
58 {
59     return m_value;
60 }
61 
62 template<class T>
63 void TreeNode<T>::setRightSibling(TreeNode<T> *pRightSibling)
64 {
65     rightSibling = pRightSibling;
66 }
67 
68 template<class T>
69 void TreeNode<T>::setLeftChild(TreeNode<T> * pLeftChild)
70 {
71     leftChild = pLeftChild;
72 }
73 
74 template<class T>
75 void TreeNode<T>::setValue(T &value)
76 {
77     m_value = va

  1 #pragma once
  2 #include <queue>
  3 #include "treeNode.h"
  4 
  5 template<class T>
  6 class Tree
  7 {
  8 public:
  9     Tree();
 10     Tree(TreeNode<T>* rt);
 11     ~Tree();
 12     //获取该树的根节点
 13     TreeNode<T>* getRoot(); 
 14     //获取节点current的父节点
 15     TreeNode<T>* Parent(TreeNode<T>* current);
 16     //获取节点t的第一个子节点，若无则返回NULL
 17     TreeNode<T>* getFirstChild(TreeNode<T>* t); 
 18     //获取节点t的下一个兄弟节点，若无则返回NULL
 19     TreeNode<T>* getNextSibling(TreeNode<T>* t);
 20     //在t节点插入一个子节点n
 21     void insertChild(TreeNode<T>* t, TreeNode<T>* n);
 22     //删除以t为根节点的子树
 23     void deleteSubTree(TreeNode<T>* t);
 24     //判断是否为空树
 25     bool isEmpty();
 26     //遍历树
 27     void OrderTraverse();
 28 
 29 private:
 30     TreeNode<T> *root, *parent;
 31     int getParent(TreeNode<T>* root,TreeNode<T>* current);
 32 };
 33 
 34 
 35 
 36 template<class T>
 37 Tree<T>::Tree()
 38 {
 39     root = parent = NULL;
 40 }
 41 
 42 template<class T>
 43 Tree<T>::Tree(TreeNode<T>* rt)
 44 {
 45     root = rt;
 46     parent = NULL;
 47 }
 48 
 49 template<class T>
 50 Tree<T>::~Tree()
 51 {
 52 
 53 }
 54 
 55 template<class T>
 56 TreeNode<T>* Tree<T>::getRoot()
 57 {
 58     return root;
 59 }
 60 
 61 template<class T>
 62 TreeNode<T>* Tree<T>::Parent(TreeNode<T>* current)
 63 {
 64     TreeNode<T> * pointer = current;
 65     TreeNode<T> *t;
 66 
 67     if (current == NULL || current == root)
 68     {
 69         return NULL;
 70     }
 71     t = root;
 72     getParent(t, pointer);
 73     return parent;
 74 }
 75 
 76 template<class T>
 77 TreeNode<T>* Tree<T>::getFirstChild(TreeNode<T>* t)
 78 {
 79     return t->getLeftChild();
 80 }
 81 
 82 template<class T>
 83 TreeNode<T>* Tree<T>::getNextSibling(TreeNode<T>* t)
 84 {
 85     return t->getRightSibling();
 86 }
 87 
 88 template<class T>
 89 void Tree<T>::insertChild(TreeNode<T>* t, TreeNode<T>* n)
 90 {
 91     if (t->getLeftChild() == NULL)
 92         t->setLeftChild(n);
 93     else
 94     {
 95         TreeNode<T>* p = t->getLeftChild();
 96         while (p->getRightSibling() != NULL)
 97             p = p->getRightSibling();
 98         p->setRightSibling(n);
 99     }
100 }
101 
102 template<class T>
103 void Tree<T>::deleteSubTree(TreeNode<T>* t)
104 {
105     if (t == root)
106     {
107         root = NULL;
108     }
109     else
110     {
111         TreeNode<T>* p = Parent(t);
112         TreeNode<T>* q = p->getLeftChild();
113         if (q == t)
114         {
115             p->setLeftChild(t->getRightSibling());
116         }
117         else
118         {
119             while (q != t)
120             {
121                 p = q;
122                 q = q->getRightSibling();
123             }
124             p->setRightSibling(q->getRightSibling());    
125         }
126     }
127 }
128 
129 template<class T>
130 int Tree<T>::getParent(TreeNode<T>* root, TreeNode<T>* current)
131 {
132     //深度优先的遍历找到current 节点
133     TreeNode<T>* q = root->getLeftChild();
134     while (q!=NULL && q!=current)
135     {
136         if (getParent(q, current) != 0)
137             return 2;
138         q = q->getRightSibling();
139     }
140 
141     if (q!=NULL && q==current)
142     {
143         parent = root;
144         return 1;
145     }
146     else
147     {
148         return 0;
149     }
150 
151 }
152 
153 template<class T>
154 bool Tree<T>::isEmpty()
155 {
156     if (NULL == root)
157         return true;
158     else
159         return false;
160 }
161 
162 template<class T>
163 void Tree<T>::OrderTraverse()
164 {
165     queue<TreeNode<T>*> q;
166     TreeNode<T>* p;
167     q.push(root);
168     while (!q.empty())
169     {
170         p = q.front();
171         if (p->getRightSibling()!=NULL)
172         {
173             q.push(p->getRightSibling());
174         }
175         if (p->getLeftChild() != NULL)
176         {
177             q.push(p->getLeftChild());
178         }
179         q.pop();
180         cout << p->getValue() << "->";
181 
182

posted @ 2018-06-15 20:03 沉舟侧畔阅读(266) 评论(0) 编辑收藏举报

刷新页面返回顶部

孤城暮雨

简单的问题复杂化，可以发现新的领域；复杂的问题简单化，可以发现新的规律。

树的浅析与实现

公告