Hard | LeetCode 85. 最大矩形 | 单调栈

85. 最大矩形

给定一个仅包含 0 和 1 、大小为 rows x cols 的二维二进制矩阵，找出只包含 1 的最大矩形，并返回其面积。

示例 1：

输入：matrix = [["1","0","1","0","0"],["1","0","1","1","1"],["1","1","1","1","1"],["1","0","0","1","0"]]
输出：6
解释：最大矩形如上图所示。

示例 2：

输入：matrix = []
输出：0

示例 3：

输入：matrix = [["0"]]
输出：0

示例 4：

输入：matrix = [["1"]]
输出：1

示例 5：

输入：matrix = [["0","0"]]
输出：0

提示：

• rows == matrix.length
• cols == matrix[0].length
• 0 <= row, cols <= 200
• matrix[i][j] 为 '0' 或 '1'

解题思路

此题和 Hard | LeetCode 84. 柱状图中最大的矩形 | 单调栈 实际上是一道题, 只不过从一维拓展到了二维上。

这道题首选要计算出每个位置(i, j)处从左往右连续的1的数量。那么对于每一列。就成了下图所示的样子。

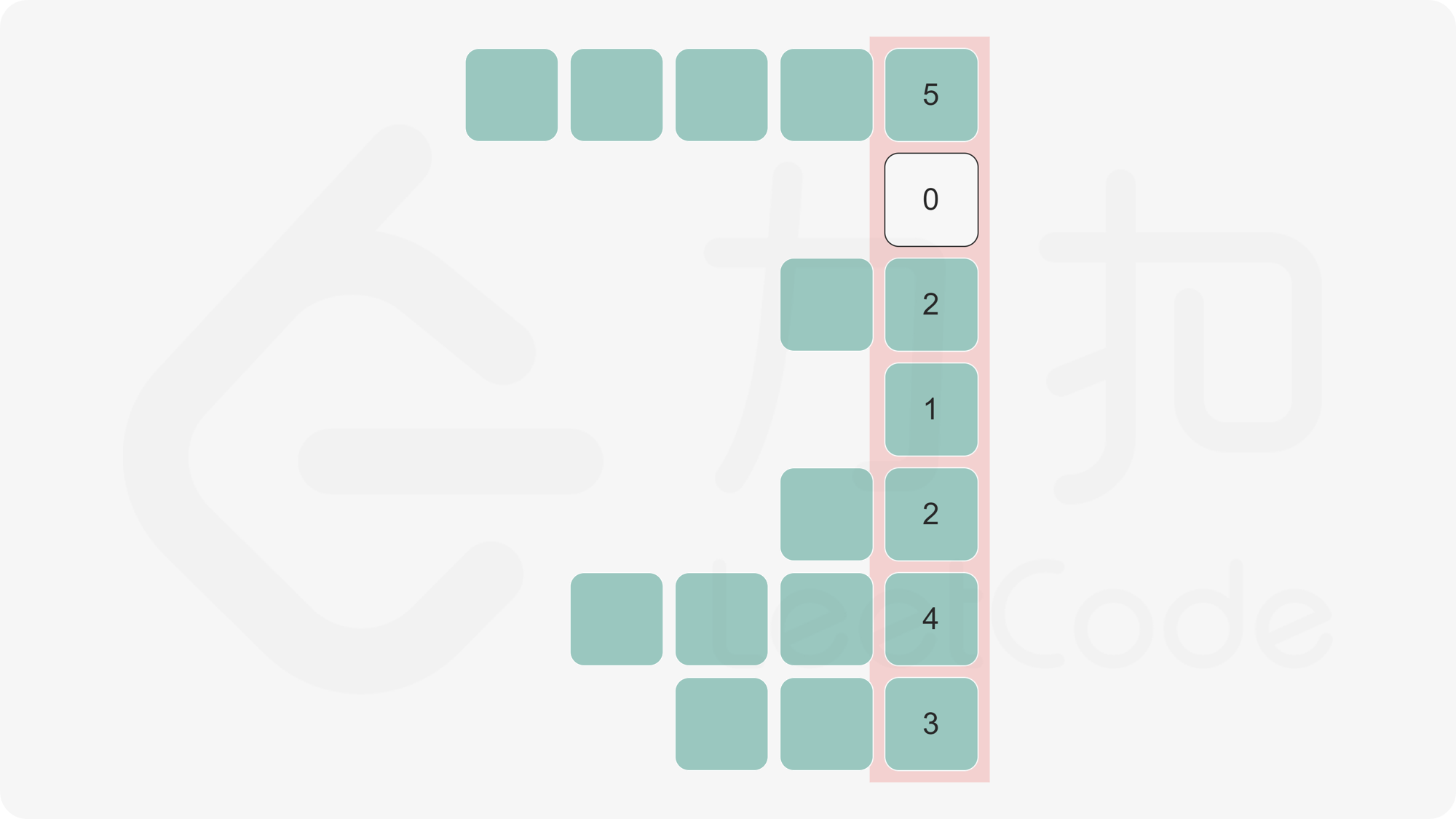
这样这道题就转化成了求柱状图中的最大的矩形。同样参考LeetCode 84题的枚举边界和单调栈的两种思路。这道题很容易写出答案。

方法一: 柱状图最大面积

public int maximalRectangle(char[][] matrix) {
    int m = matrix.length;
    if (m == 0) {
        return 0;
    }
    int n = matrix[0].length;
    // 新建一个二维数组
    int[][] left = new int[m][n];

    for (int i = 0; i < m; i++) {
        for (int j = 0; j < n; j++) {
            // 计算matrix[i][j] 左侧连续的数字1的数量
            if (matrix[i][j] == '1') {
                left[i][j] = (j == 0 ? 0 : left[i][j - 1]) + 1;
            }
        }
    }
    // 使用枚举边界的方法, 求出柱形图的最大面积
    int ret = 0;
    for (int i = 0; i < m; i++) {
        for (int j = 0; j < n; j++) {
            if (matrix[i][j] == '0') {
                continue;
            }
            // 计算以[i, j]为右下角的最大矩形,
            // 也就是说以当前的i作为起始边界
            int width = left[i][j];
            int area = width;
            // 然后遍历[0, i]的所有left值作为边界
            for (int k = i - 1; k >= 0; k--) {
                width = Math.min(width, left[k][j]);
                // 不断更新面积的最大值
                area = Math.max(area, (i - k + 1) * width);
            }
            ret = Math.max(ret, area);
        }
    }
    return ret;
}

方法二: 单调栈

public int maximalRectangle(char[][] matrix) {
    int m = matrix.length;
    if (m == 0) {
        return 0;
    }
    int n = matrix[0].length;
    int[][] left = new int[m][n];

    for (int i = 0; i < m; i++) {
        for (int j = 0; j < n; j++) {
            if (matrix[i][j] == '1') {
                left[i][j] = (j == 0 ? 0 : left[i][j - 1]) + 1;
            }
        }
    }

    int ret = 0;
    // 对于每一列，使用基于柱状图的方法
    for (int j = 0; j < n; j++) {

        // 分别找出上面和下面的临界点
        int[] up = new int[m];
        int[] down = new int[m];
        Arrays.fill(down, m);
        ArrayDeque<Integer> stack = new ArrayDeque<>();
        for (int i = 0; i < m; i++) {
            while (!stack.isEmpty() && left[stack.peek()][j] >= left[i][j]) {
                down[stack.pop()] = i;
            }
            up[i] = stack.isEmpty() ? -1 : stack.peek();
            stack.push(i);
        }

        for (int i = 0; i < m; i++) {
            int height = down[i] - up[i] - 1;
            int area = height * left[i][j];
            ret = Math.max(ret, area);
        }
    }
    return ret;
}