Hard | LeetCode 4. 寻找两个正序数组的中位数 | 二分法

4. 寻找两个正序数组的中位数

给定两个大小分别为 m 和 n 的正序（从小到大）数组 nums1 和 nums2。请你找出并返回这两个正序数组的 中位数 。

示例 1：

输入：nums1 = [1,3], nums2 = [2]
输出：2.00000
解释：合并数组 = [1,2,3] ，中位数 2

示例 2：

输入：nums1 = [1,2], nums2 = [3,4]
输出：2.50000
解释：合并数组 = [1,2,3,4] ，中位数 (2 + 3) / 2 = 2.5

示例 3：

输入：nums1 = [0,0], nums2 = [0,0]
输出：0.00000

示例 4：

输入：nums1 = [], nums2 = [1]
输出：1.00000

示例 5：

输入：nums1 = [2], nums2 = []
输出：2.00000

提示：

• nums1.length == m
• nums2.length == n
• 0 <= m <= 1000
• 0 <= n <= 1000
• 1 <= m + n <= 2000
• -106 <= nums1[i], nums2[i] <= 106

进阶：你能设计一个时间复杂度为 O(log (m+n)) 的算法解决此问题吗？

解题思路

方法一： 二分划分法

目标是求取中位数, 很自然能够想到将这两个数组分成两部分。这两部分的数组元素数量大致相同。并且一个数组的所有元素小于另外一个数组的所有元素。

数组本身是有序的。那么只需要在第一个元素找到一个划分的点, 然后第二个数组的划分点根据两数组总元素个数和第一个划分点就能够自动确定。问题在于如何判定, 是否找到了划分的那个点。

判断方法： 两个数组划分点左边的元素交叉小于划分点右边的元素。

只要满足上面那个条件, 就得到了一个正确的划分, 那么就可以返回结果了。

如果得到了不正确的划分, 该如何做调整呢？这就是此问题的关键。

以下是两种错误的划分

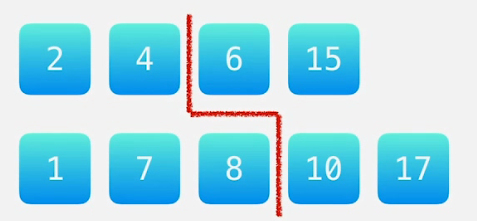
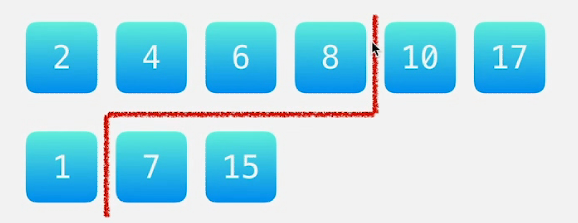
对于第一种而言, 第一个数组分隔线左边元素 小于 第二个数组分隔线右边元素, 这个条件是满足的
但是 第二个数组分隔线左边元素 小于第一个数组分隔线右边元素, 这个条件不满足。

这种情况, 由于第一个数组分隔线右边的元素过小, 所以第一个数组分隔线需要向右移动。
同理, 上图的右边的一张图第一个数组分隔线需要向左移动。

这就是二分的原则。

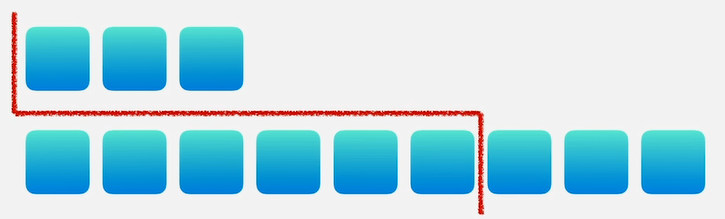
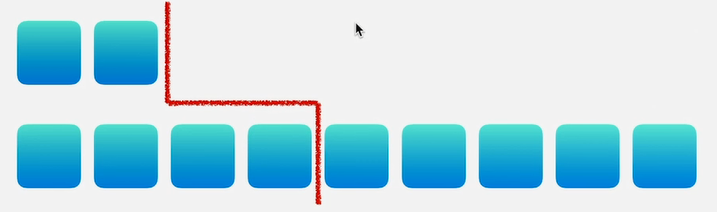
当然此题还要考虑一下几种分隔线的临界情况。分隔线左边和右边没有元素。

基于以上我们需要分隔线左边交叉小于分隔线右边的需求。

所以我们需要将分隔线左边临界的元素赋值为负无穷, 将分隔线右边临界的元素是正无穷, 这样就能保证分隔线左边交叉小于分隔线右边了。

public double findMedianSortedArrays(int[] nums1, int[] nums2) {
    if (nums1.length < nums2.length) {
        int[] temp = nums1;
        nums1 = nums2;
        nums2 = temp;
    }
    int m = nums1.length;
    int n = nums2.length;
    int leftSize = (m + n + 1) >> 1;
    int left = 0, right = m;
    while (left <= right) {
        // i表示第一个数组的分隔线, 范围是[0, m]
        int i = (left + right) >> 1;
        // j表示第二个数组的分隔线, 其位置依赖于i, 因为要保证分隔线两边的元素个数几乎相等
        int j = leftSize - i;
        if (get(nums1, i - 1) > get(nums2, j)) {
            // 第一个数组分隔线左边元素 大于第二个数组分隔线右边元素
            // 则说明第一个数组分隔线太大了
            right = i - 1;
        } else if (get(nums2, j - 1) > get(nums1, i)) {
            // 第二个数组分隔线左边元素 大于第一个数组分隔线右边元素
            // 则说明第二个数组分隔线太小了
            left = i + 1;
        } else {
            // 不可能存在交叉大于的情况
            // 所以以上两个条件不满足, 一定是满足交叉小于的条件
            if (((m + n) & 1) == 0) {
                // 两个数组总长度是偶数
                return (
                    // 返回分隔线左边元素最大值和右边元素最小值的平均值
                        Math.max(get(nums1, i - 1), get(nums2, j - 1)) +
                        Math.min(get(nums1, i), get(nums2, j))
                ) * 1.0 / 2;
            } else {
                // 数组总长度为奇数时, 直接返回分隔线左边的元素的最大值
                return Math.max(get(nums1, i - 1), get(nums2, j - 1));
            }
        }
    }
    return 0;
}

private int get(int[] nums, int index) {
    if (index < 0) {
        return Integer.MIN_VALUE;
    } else if (index >= nums.length) {
        return Integer.MAX_VALUE;
    } else {
        return nums[index];
    }
}

以上的代码注意到 在二分的时候, 只判断了一个交叉大于的情况, 就进行了二分。因为默认另一个移动是交叉小于的。

那么存不存在两个数组同时出现交叉大于的情况呢?这种情况是不会出现的。所以整个划分过程只有三种情况

1. 第一个数组分隔线左边 小于 第二个数组分隔线右边,
   但是第二个数组分隔线左边 大于 第一个数组分隔线右边,

2. 第二个数组分隔线左边 小于 第一个数组分隔线右边,
   但是第一个数组分隔线左边 大于 第二个数组分隔线右边,

3. 两个数组均满足分隔线处交叉小于的情况。