Medium | LeetCode 621. 任务调度器 | 设计
621. 任务调度器
给你一个用字符数组 tasks 表示的 CPU 需要执行的任务列表。其中每个字母表示一种不同种类的任务。任务可以以任意顺序执行,并且每个任务都可以在 1 个单位时间内执行完。在任何一个单位时间,CPU 可以完成一个任务,或者处于待命状态。
然而,两个 相同种类 的任务之间必须有长度为整数 n 的冷却时间,因此至少有连续 n 个单位时间内 CPU 在执行不同的任务,或者在待命状态。
你需要计算完成所有任务所需要的 最短时间 。
示例 1:
输入:tasks = ["A","A","A","B","B","B"], n = 2
输出:8
解释:A -> B -> (待命) -> A -> B -> (待命) -> A -> B
在本示例中,两个相同类型任务之间必须间隔长度为 n = 2 的冷却时间,而执行一个任务只需要一个单位时间,所以中间出现了(待命)状态。
示例 2:
输入:tasks = ["A","A","A","B","B","B"], n = 0
输出:6
解释:在这种情况下,任何大小为 6 的排列都可以满足要求,因为 n = 0
["A","A","A","B","B","B"]
["A","B","A","B","A","B"]
["B","B","B","A","A","A"]
...
诸如此类
示例 3:
输入:tasks = ["A","A","A","A","A","A","B","C","D","E","F","G"], n = 2
输出:16
解释:一种可能的解决方案是:
A -> B -> C -> A -> D -> E -> A -> F -> G -> A -> (待命) -> (待命) -> A -> (待命) -> (待命) -> A
提示:
1 <= task.length <= 104tasks[i]是大写英文字母n的取值范围为[0, 100]
解题思路
方法一: 暴力模拟
选取任务的原则, 选择当前不在冷却期内(立即可运行的)剩余任务数量最多的任务。
使用两个数组, 分别维护数组的下一次执行的最早时间, 以及剩余的任务的数量。每次按照上面所说的原则去挑选任务, 然后选择到任务之后, 更新被选择任务的下一次运行的最早时间和剩余的任务数量。如此循环往复即可。
public int leastInterval(char[] tasks, int n) {
// 统计任务的数量
Map<Character, Integer> freq = new HashMap<>();
for (char ch : tasks) {
freq.put(ch, freq.getOrDefault(ch, 0) + 1);
}
// 将HashMap变换为两个List,
// 分别用来保存任务的下一次的执行最早时间以及剩余任务数量
// 具体的任务名称丢弃
int m = freq.size();
List<Integer> nextValid = new ArrayList<>();
List<Integer> rest = new ArrayList<>();
for (Map.Entry<Character, Integer> entry : freq.entrySet()) {
// 初始时将下一次执行的最早时间设置为1
nextValid.add(1);
rest.add(entry.getValue());
}
// 每次挑选任务的原则是 选择不在冷却中并且剩余执行次数最多的那个任务
int time = 0;
for (int i = 0; i < tasks.length; ++i) {
++time;
// 在下次运行时间最早的那个时间点
int minNextValid = Integer.MAX_VALUE;
for (int j = 0; j < m; ++j) {
if (rest.get(j) != 0) {
minNextValid = Math.min(minNextValid, nextValid.get(j));
}
}
// 决定是否需要直接更新当前时间到下次最早的时间
time = Math.max(time, minNextValid);
// 从符合当前最早时间之内的任务里找出剩余任务最大的任务
int best = -1;
for (int j = 0; j < m; ++j) {
if (rest.get(j) != 0 && nextValid.get(j) <= time) {
if (best == -1 || rest.get(j) > rest.get(best)) {
best = j;
}
}
}
// 然后将这个任务的接下来的最早时间改为冷却后的时间
nextValid.set(best, time + n + 1);
// 并且将这个任务的剩余数量减1
rest.set(best, rest.get(best) - 1);
}
return time;
}
方法二: 找规律
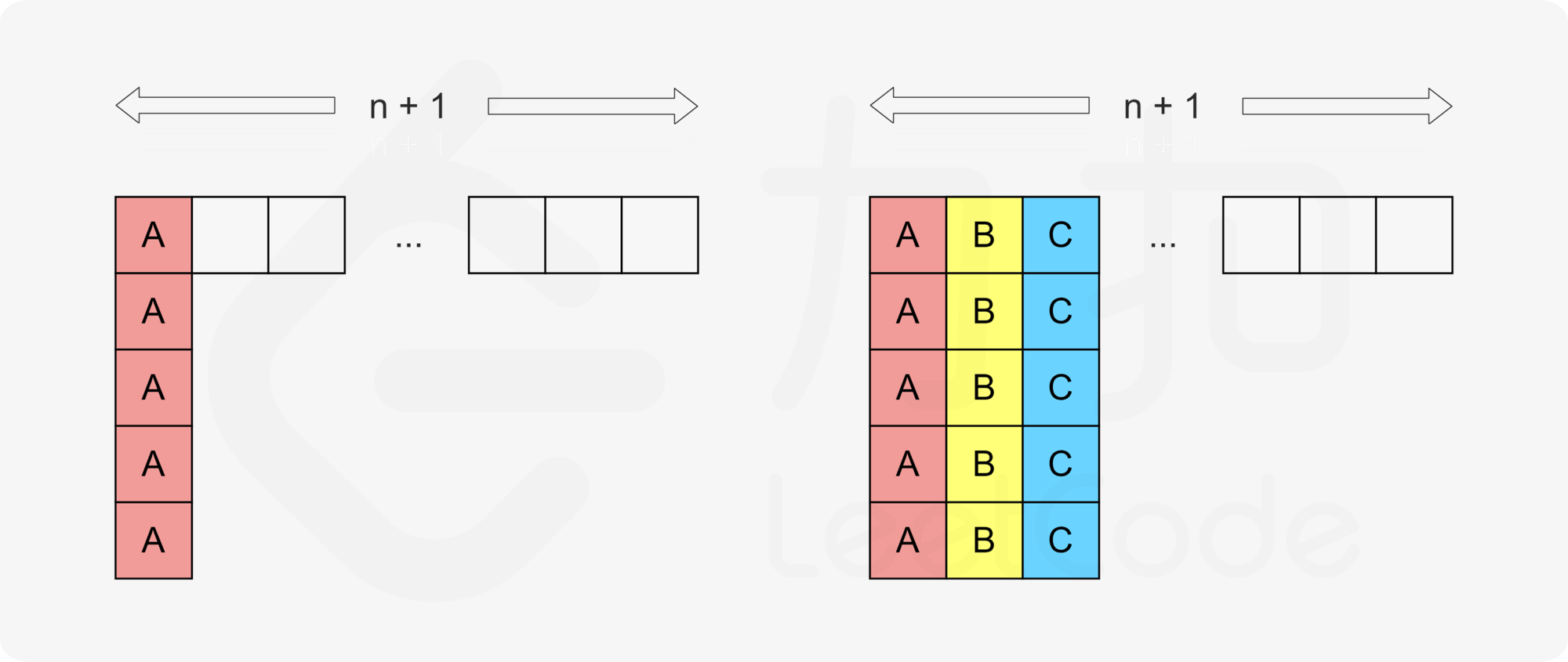
首先我们排列任务时, 按照这样的方式排列。加入这N+1列够用, 排不满的情况下, 那么最大的所需时长就是\((\operatorname{maxExec}-1)(n+1)+\operatorname{maxCount}\) 。这种就很容易想。
但是, 如果如果按照这种方式排, N+1列不够用, 那该怎么办呢?
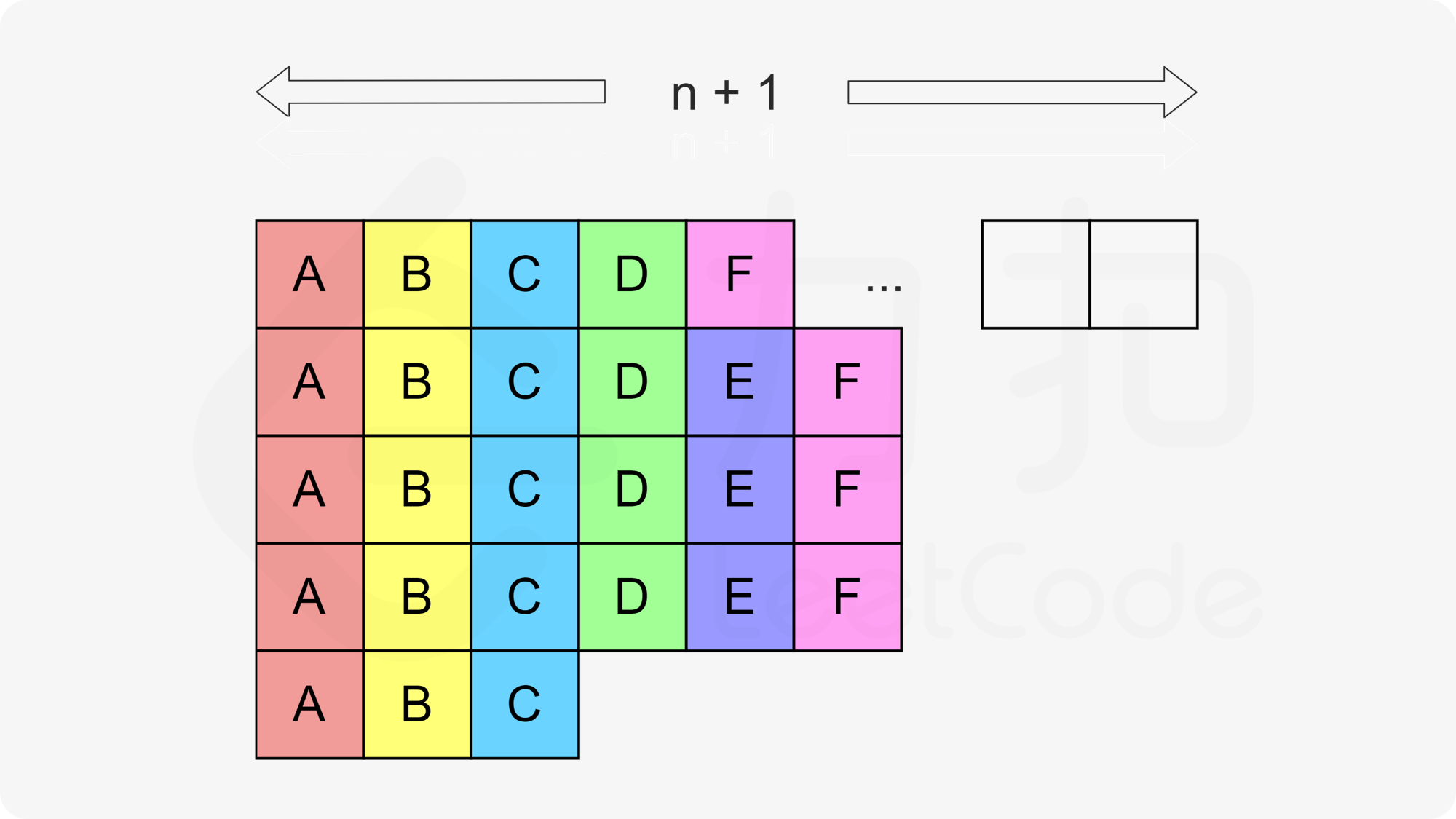
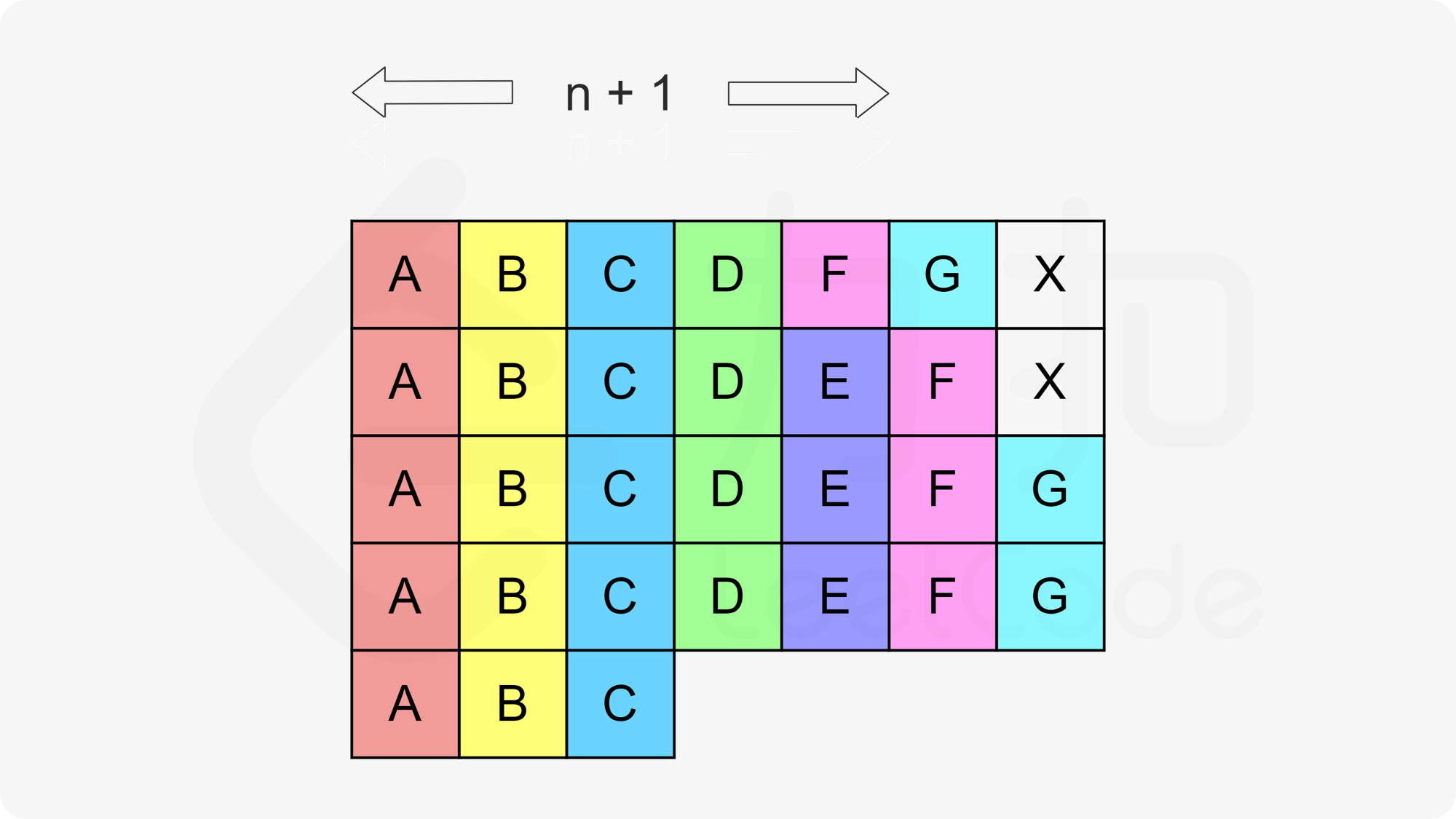
当N+1不够用的时候, 像这样排, 这样的话, 由于任务种类比较多, 就不必等待冷却时间了, 所以最终的任务总运行时间就是task.length
public int leastInterval2(char[] tasks, int n) {
Map<Character, Integer> freq = new HashMap<Character, Integer>();
// 最多的执行次数
int maxExec = 0;
for (char ch : tasks) {
int exec = freq.getOrDefault(ch, 0) + 1;
freq.put(ch, exec);
maxExec = Math.max(maxExec, exec);
}
// 具有最多执行次数的任务数量(这里是任务种类的数量)
int maxCount = 0;
for (Map.Entry<Character, Integer> entry : freq.entrySet()) {
if (entry.getValue() == maxExec) {
++maxCount;
}
}
return Math.max((maxExec - 1) * (n + 1) + maxCount, tasks.length);
}


