Easy | LeetCode 190. 颠倒二进制位 | 位运算

190. 颠倒二进制位

颠倒给定的 32 位无符号整数的二进制位。

示例 1：

输入: 00000010100101000001111010011100
输出: 00111001011110000010100101000000
解释: 输入的二进制串 00000010100101000001111010011100 表示无符号整数 43261596，
     因此返回 964176192，其二进制表示形式为 00111001011110000010100101000000。

示例 2：

输入：11111111111111111111111111111101
输出：10111111111111111111111111111111
解释：输入的二进制串 11111111111111111111111111111101 表示无符号整数 4294967293，
     因此返回 3221225471 其二进制表示形式为 10111111111111111111111111111111 。

提示：

• 请注意，在某些语言（如 Java）中，没有无符号整数类型。在这种情况下，输入和输出都将被指定为有符号整数类型，并且不应影响您的实现，因为无论整数是有符号的还是无符号的，其内部的二进制表示形式都是相同的。
• 在 Java 中，编译器使用二进制补码记法来表示有符号整数。因此，在上面的 示例 2 中，输入表示有符号整数 -3，输出表示有符号整数 -1073741825。

解题思路

方法一： 逐位颠倒

public int reverseBits(int n) {
    int res = 0;
    for (int i = 0; i <= 31; i++) {            
        res |= (n & (1 << i)) != 0 ? 1 << (31 - i) : 0;
    }
    return res;
}

方法二： 按字节颠倒

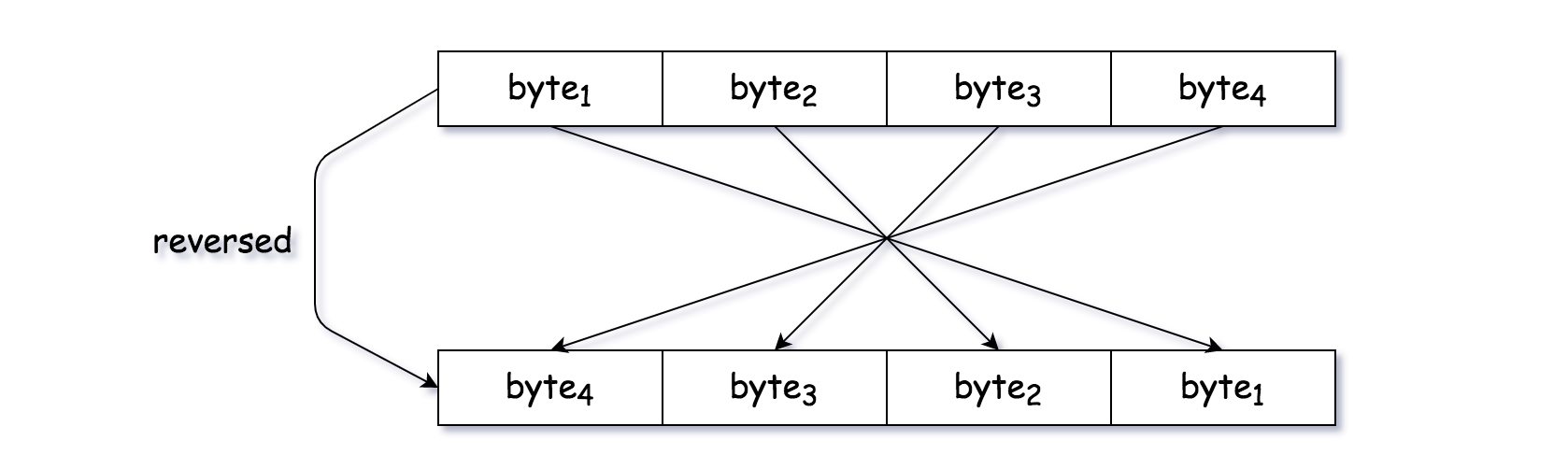
有一种完全基于算术和位操作，不基于任何循环语句可以反转一个字节。以下是逐个反转字节的解法。

class Solution {

    private final HashMap<Byte, Byte> cache = new HashMap<>();

    public int reverseBits(int n) {
        int res = 0;
        int power = 24;
        while (n > 0) {
            res += reverseByte(n & 0xff) << power;
            n = n >> 8;
            power -= 8;
        }
        return res;
    }

    public int reverseByte(int nByte) {
        if (!cache.containsKey(nByte)) {
            cache.put(nByte, ((nByte * 0x0202020202) & 0x010884422010) % 1023);
        }
        return cache.get(nByte);
    }
}

方法三： 分治算法

public int reverseBits(int n) {
    // 先反转左边16位和右边16位
    n = (n >>> 16) | (n << 16);
    // 然后反转左右两边16位的8位
    n = ((n & 0xff00ff00) >>> 8) | ((n & 0x00ff00ff) << 8); 
    // 接着反转8位的左右四位
    n = ((n & 0xf0f0f0f0) >>> 4) | ((n & 0x0f0f0f0f) << 4); 
    // 反转4位的左右两位
    n = ((n & 0xcccccccc) >>> 2) | ((n & 0x33333333) << 2);
    // 反转左右两位的各一位
    n = ((n & 0xaaaaaaaa) >>> 1) | ((n & 0x55555555) << 1); 
    return n;
}