Medium | LeetCode 322. 零钱兑换 | 动态规划 (递归 | 迭代)

322. 零钱兑换

给定不同面额的硬币 coins 和一个总金额 amount。编写一个函数来计算可以凑成总金额所需的最少的硬币个数。如果没有任何一种硬币组合能组成总金额，返回 -1。

你可以认为每种硬币的数量是无限的。

示例 1：

输入：coins = [1, 2, 5], amount = 11
输出：3 
解释：11 = 5 + 5 + 1

示例 2：

输入：coins = [2], amount = 3
输出：-1

示例 3：

输入：coins = [1], amount = 0
输出：0

示例 4：

输入：coins = [1], amount = 1
输出：1

示例 5：

输入：coins = [1], amount = 2
输出：2

提示：

• 1 <= coins.length <= 12
• 1 <= coins[i] <= 231 - 1
• 0 <= amount <= 104

解题思路

刚看到题目以为这道题是一到贪心问题, 因为在我们现实生活的场景下： 100元人民币, 50元, 20元, 10元, 5元, 1元这样, 这种问题就类似于去商店买东西, 店主找零钱给你。所以自然想到贪心的原则, 每次尽可能给大面额的货币。

于是依据贪心的原则写出了如下的代码

public int coinChange(int[] coins, int amount) {
    if (coins.length == 0) {
        return -1;
    }
    Arrays.sort(coins);
    int index = coins.length - 1;
    int res = 0;
    while(amount > 0) {
        if (amount >= coins[index]) {
            // 当前最大金额能用, 就用当前的最大金额
            amount -= coins[index];
            res++;
        } else if (index > 0) {
            // 不能用了, 就用次大的金额
            index--;
        } else {
            // 所有的金额都不能用, 则返回-1
            return -1;
        }
    }
    return res;
}

这种思路是错的, 因为贪心的原则, 使用的金额一定能大就大。这样就有可能出现, 本来是可以组合的, 但是贪心得使用了大金额, 导致没法组合。比如有硬币 10, 6, 5, 2, 要求组合总金额为11, 依据上述贪心的原则, 则不能组合成11。

方法一： 递归(深度优先遍历)

如下图

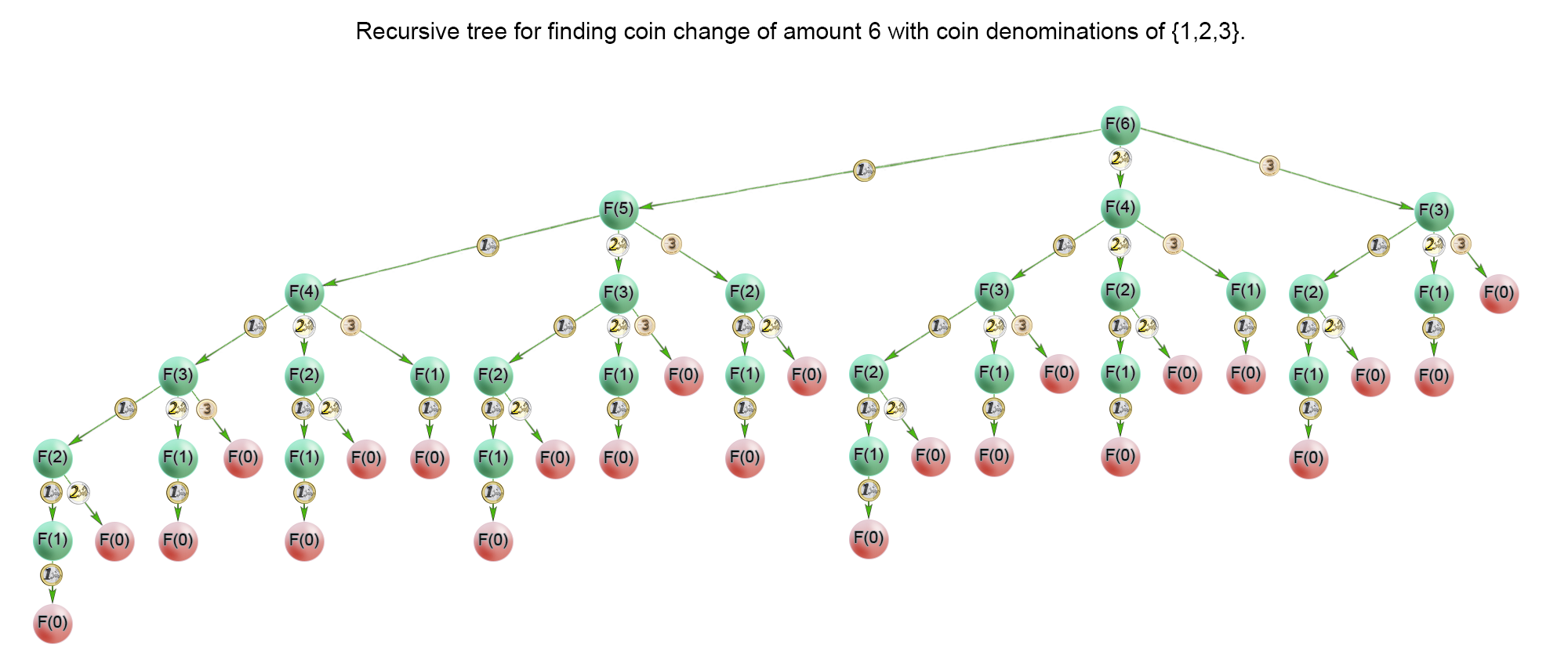
本质是暴力枚举所有的情况。

public int coinChange(int[] coins, int amount) {
    if (amount < 1) {
        return 0;
    }
    return coinChange(coins, amount, new int[amount]);
}
/**
 * count[i]表示组成总金额i需要的最小的硬币数
 */
private int coinChange(int[] coins, int rem, int[] count) {
    if (rem < 0) {
        // 这种表示没有办法组合成总金额
        return -1;
    }
    if (rem == 0) {
        // 递归出口, 所给硬币能够组合成总金额
        return 0;
    }
   
    if (count[rem - 1] != 0) {
        // 如果rem已经被计算过, 则直接返回, 避免重复计算
        return count[rem - 1];
    }
    int min = Integer.MAX_VALUE;
    // 遍历所有的硬币, 尝试使用当前硬币
    for (int coin : coins) {
        int res = coinChange(coins, rem - coin, count);
        if (res >= 0 && res < min) {
            // res >= 0, 表示可以组成所给的金额 
            // res < min , 表示即使可以组成所给金额, 
            // 但是不是一个更优的方式, 也可看做不能组成所给金额
            min = 1 + res;
        }
    }
    // 所有硬币都是用了, 但是没有办法自核成总金额, 则将当前组成金额的最小硬币数设置为-1
    count[rem - 1] = (min == Integer.MAX_VALUE) ? -1 : min;
    return count[rem - 1];
}

方法二： 动态规划

方法一是自上而下的递归的方式, 大多数这种自上而下的都有自下而上的迭代的版本。并且这种自下而上的方法一般就是在填一张二维表格, 也就是动态规划算法。

定义 F(i)为组成金额 i 所需最少的硬币数量, 状态转移方程为

\[F(i)=\min _{j=0 . . . n-1} F\left(i-c_{j}\right)+1 \]

public int coinChange(int[] coins, int amount) {
    int max = amount + 1;
    int[] dp = new int[amount + 1];
    // 相当于设置初始值为无穷大
    Arrays.fill(dp, max);
    dp[0] = 0;
    for (int i = 1; i <= amount; i++) {
        // 枚举所有硬币
        for (int j = 0; j < coins.length; j++) {
            if (coins[j] <= i) {
                // 并尝试使用所有硬币
                dp[i] = Math.min(dp[i], dp[i - coins[j]] + 1);
            }
        }
    }
    return dp[amount] > amount ? -1 : dp[amount];
}