Medium | LeetCode 426 | 剑指 Offer 36. 二叉搜索树与双向链表 | 中序遍历(递归)
剑指 Offer 36. 二叉搜索树与双向链表
输入一棵二叉搜索树,将该二叉搜索树转换成一个排序的循环双向链表。要求不能创建任何新的节点,只能调整树中节点指针的指向。
为了让您更好地理解问题,以下面的二叉搜索树为例:
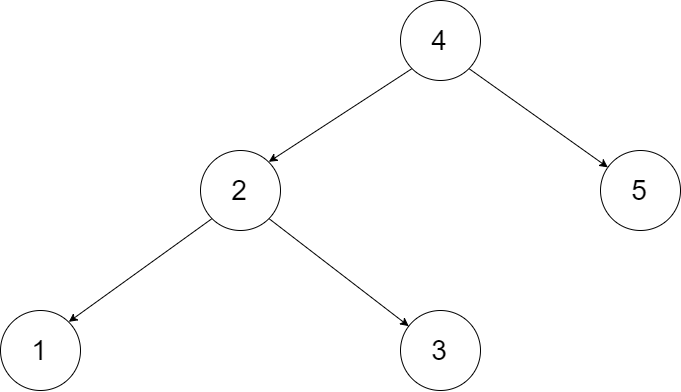
我们希望将这个二叉搜索树转化为双向循环链表。链表中的每个节点都有一个前驱和后继指针。对于双向循环链表,第一个节点的前驱是最后一个节点,最后一个节点的后继是第一个节点。
下图展示了上面的二叉搜索树转化成的链表。“head” 表示指向链表中有最小元素的节点。
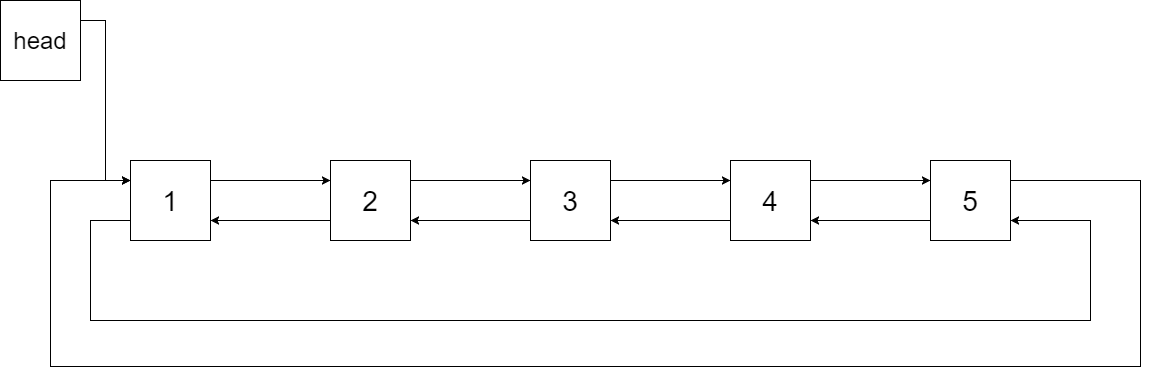
特别地,我们希望可以就地完成转换操作。当转化完成以后,树中节点的左指针需要指向前驱,树中节点的右指针需要指向后继。还需要返回链表中的第一个节点的指针。
解体思路
方法一: 中序遍历
这道题很容易想到二叉搜索树的中序遍历序列就是一个递增有序的序列。所以这道题很简单, 只要在中序遍历的时候, 保存上一个访问节点的指针就可以了。在遍历访问当前元素的时候, 对上一个节点和当前节点的指针进行操作即可。
双向链表的结构和二叉树节点结构基本一致, 都有两个指针类型和一个值类型。二叉树节点两个指针left和right分别指向左孩子和右孩子, 双向链表节点的两个指针pre, next分别指向前驱和后继。结构上二叉排序树和双向链表本是相统一的。
private Node pre, head;
public Node treeToDoublyList(Node root) {
if (root == null) {
return null;
}
// 中序遍历二叉树, 遍历的同时修改遍历访问节点和前驱节点指针, 将其串成一个双向链表
inOrderTranverse(root);
// 双向循环链表, 将头结点和尾节点连接起来
head.left = pre;
pre.right = head;
return head;
}
public void inOrderTranverse(Node root) {
if (root == null) {
return;
}
// 先递归遍历左子树
inOrderTranverse(root.left);
// 访问当前根节点
if (pre == null) {
// pre == null, 代表是第一个节点, 所以需要把头结点保存起来
head = root;
} else {
// 将前驱节点的right指针指向当前元素
pre.right = root;
}
//将当前元素的left指针指向前一个元素
root.left = pre;
// 串起来之后, 将当前访问的节点作为pre, 然后访问下一个节点
pre = root;
inOrderTranverse(root.right);
}
方法二: 递归(先序遍历)
每次递归子树时, 返回子树变成链表后的最左边节点和最右边节点。
public TreeNode treeToDoublyList(TreeNode root) {
if (root == null) {
return null;
}
TreeNode[] res = toList(root);
res[0].left = res[1];
res[1].right = res[0];
return res[0];
}
public TreeNode[] toList(TreeNode root) {
if (root == null) {
return new TreeNode[2];
}
// 将左右子树变成链表
TreeNode[] left = toList(root.left);
TreeNode[] right = toList(root.right);
// 将左子树链表的尾节点的右指针指向当前元素
if (left[1] != null) {
left[1].right = root;
}
// 将右子树链表的头节点的左指针指向当前元素
if (right[0] != null) {
right[0].left = root;
}
// 将当前元素的左右指针分别指向左子树链表的尾节点和右子树链表的头结点
root.left = left[1];
root.right = right[0];
// 返回当前链表的尾节点和头结点
if (left[0] != null && right[1] != null) {
return new TreeNode[]{left[0], right[1]};
} else if (left[0] != null) {
return new TreeNode[]{left[0], root};
} else if (right[1] != null) {
return new TreeNode[]{root, right[1]};
} else {
return new TreeNode[]{root, root};
}
}


