Hard | 剑指 Offer 43. 1~n 整数中 1 出现的次数
Hard | 剑指 Offer 43. 1~n 整数中 1 出现的次数
输入一个整数 n ,求1~n这n个整数的十进制表示中1出现的次数。
例如,输入12,1~12这些整数中包含1 的数字有1、10、11和12,1一共出现了5次。
示例 1:
输入:n = 12
输出:5
示例 2:
输入:n = 13
输出:6
限制:
1 <= n < 2^31
这道Hard题, 思路非常巧妙。他的核心思想是计算每个位当中数字1出现的个数。计算方法是, 固定某个位为1, 然后变换其他位, 并且, 其他位可以看做一个N-1位数。然后看这个N-1位数的取值范围, 从而得到当前位为1的个数。
根据当前位的数字不同, 有三种可能的情况分类:
-
当 cur = 0 时: 此位 11 的出现次数只由高位 high 决定,计算公式为:high * digit
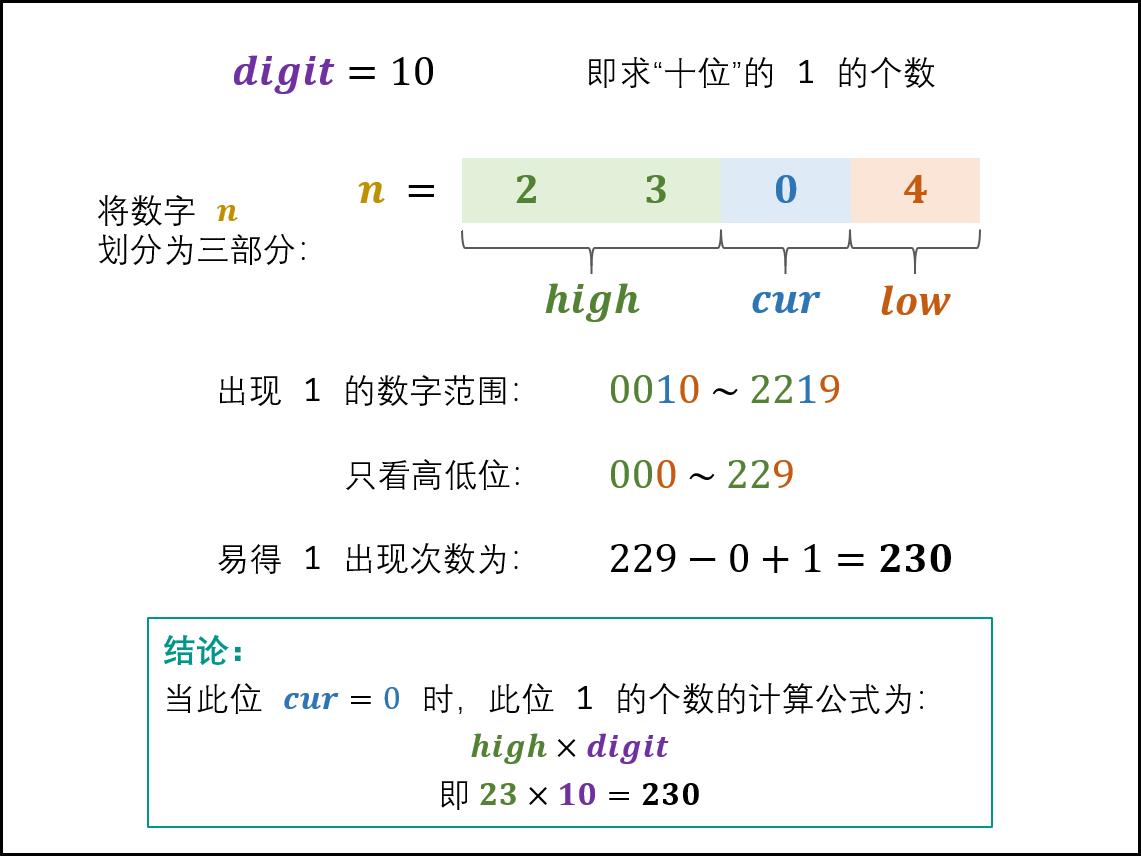
-
当 cur = 1时: 此位 11 的出现次数由高位 high和低位 low决定,计算公式为:high * digit + low + 1;
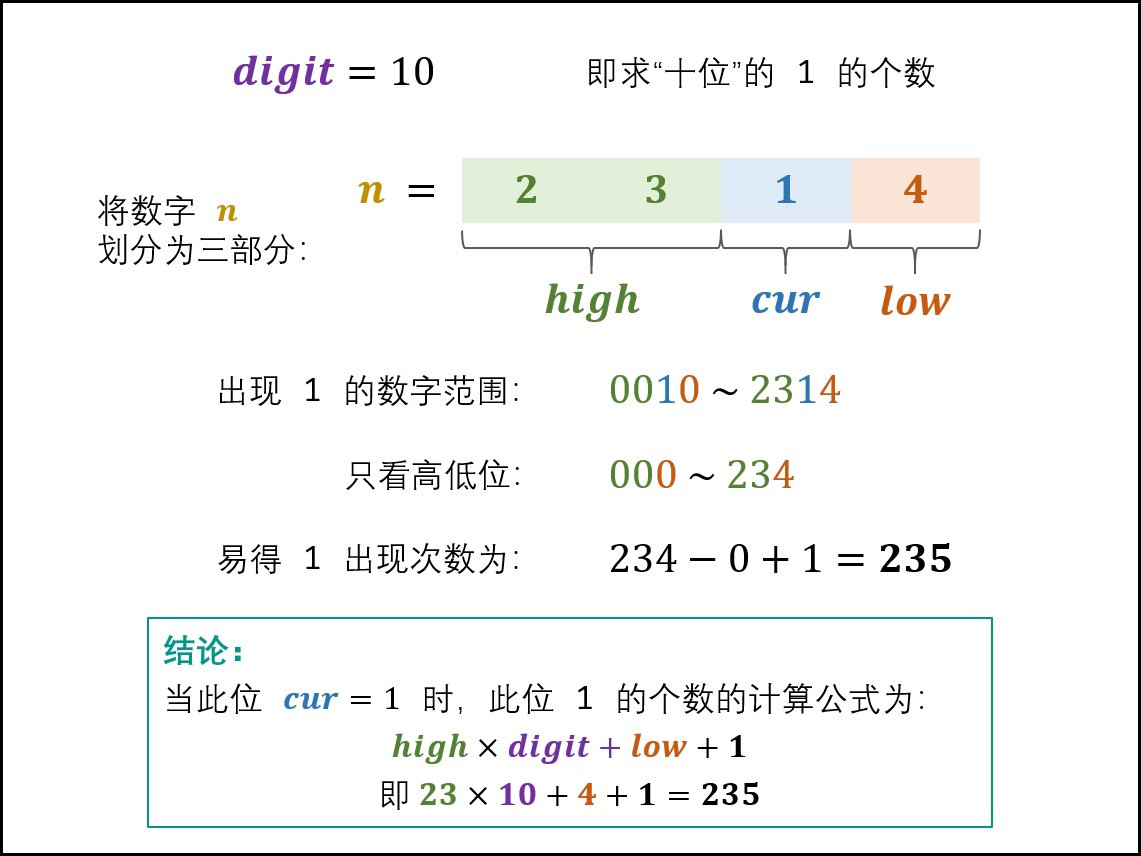
-
当 cur = 2,3,⋯,9 时: 此位 1 的出现次数只由高位 high决定,计算公式为:(high + 1) * digit
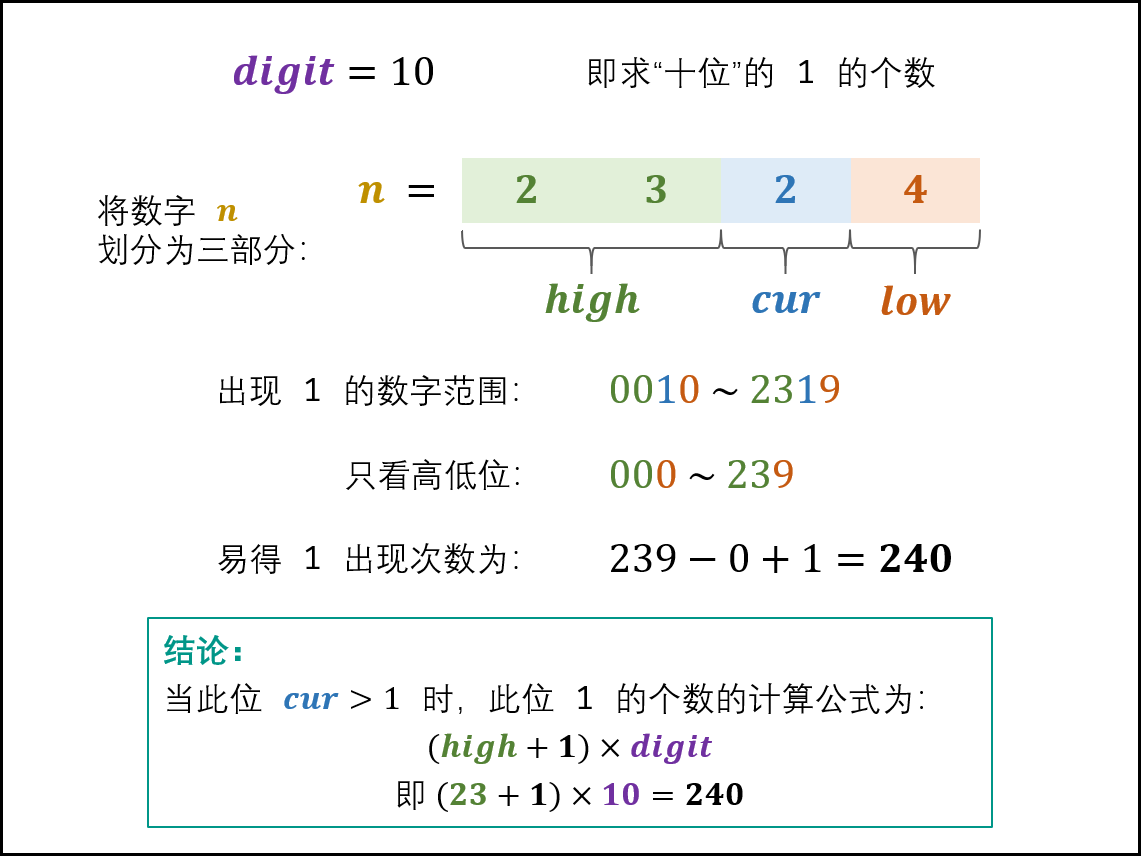
根据以上的几个特点, 只要遍历每一位, 遍历每一位时, 更新High值, Low值, Cur值, 进行相应的公式计算, 进行加总, 就可以得到相应的答案。
public int countDigitOne(int n) {
int digit = 1;
int res = 0;
// 从个位数开始, 初始化高位值, 低位值, 当前位数字
int high = n / 10;
int low = 0;
int cur = n % 10;
// 从最低位逐渐向最高位迭代
while(high != 0 || cur != 0) {
if (cur == 0) {
res += high * digit;
} else if (cur == 1) {
res += (high * digit + low + 1);
} else {
res += (high + 1) * digit;
}
// 更新高位, 低位, 当前位值, 此时更新可以根据前一个值迭代计算
low += cur * digit;
cur = high % 10;
high /= 10;
digit *= 10;
}
return res;
}


