Hard | 剑指 Offer 51. 数组中的逆序对 | 归并排序
在数组中的两个数字,如果前面一个数字大于后面的数字,则这两个数字组成一个逆序对。输入一个数组,求出这个数组中的逆序对的总数。
示例 1:
输入: [7,5,6,4]
输出: 5
方法一: 归并排序
这道Hard题是很难想的。方法很巧妙, 我是看了题解看了好长时间才弄懂。
这道题的核心思想是
递归的把数据分成两半, 先计算左半边的逆序对, 再计算右半边的逆序对, 然后计算跨越左半边和右半边的逆序对。
计算逆序对的办法是归并排序。边排序, 边计算。并且在计算跨左右两边的逆序对 , 并且归并排序的同时, 有一个重要的前提是左右两边的逆序对已经计算完成了,并且已经是升序的。
下图1是递归分治的过程, 简单来说就是递归的归并排序算法
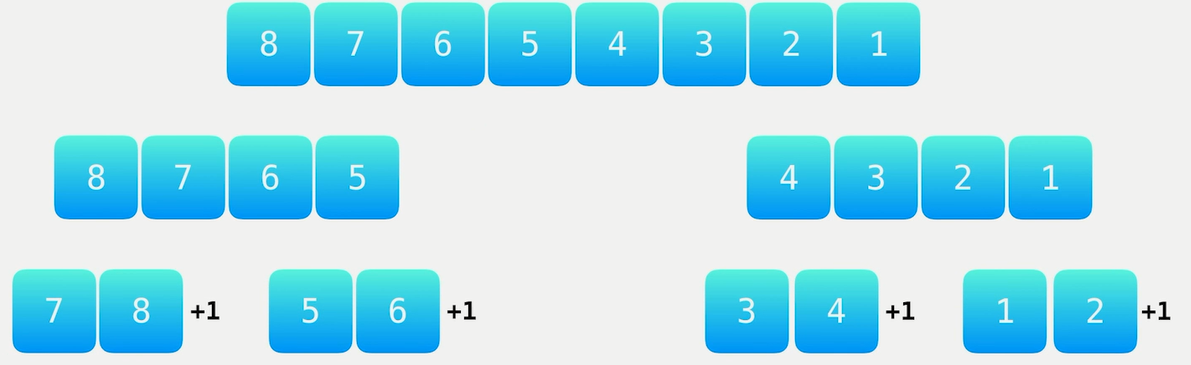
图2是归并排序并且计算逆序对的过程。首先是2和1比, 因为1小于2, 所以把1放入原始数据(代表已排好序)。由于(由于此时2和1构成逆序对)。根据归并的两个数组有序的特点, 一下了就可以得出, 在左边的数组当中, 与右边1构成逆序对的数是4。把这个过程画一画, 就能感受到时间的优化在哪里了。
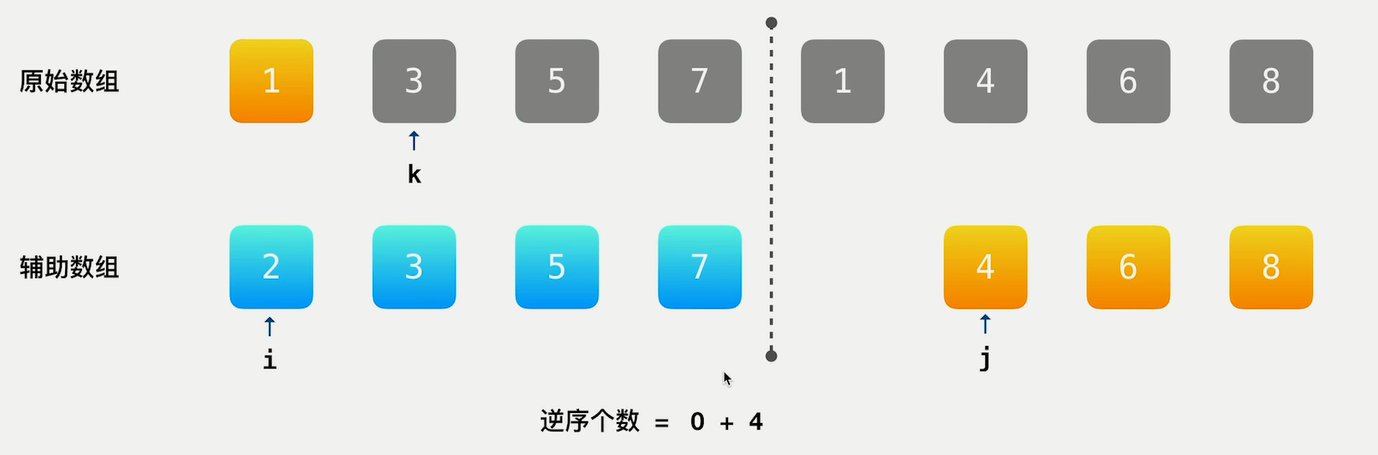
总的时间复杂度为:O(nlogn); 空间复杂度为O(n)
首先, 先把归并排序的代码写出来
public int[] mergeSort(int[] nums) {
int l = 0, r = nums.length - 1;
int[] copy = Arrays.copyOf(nums, nums.length);
int[] temp = new int[nums.length];
mergeSortCore(copy, 0, nums.length - 1, temp);
return copy;
}
public void mergeSortCore(int[] nums, int left, int right, int[] temp) {
if (left >= right) {
return;
}
// 先将数组切分成两半, 递归的归并这两个一半的数组
int mid = (left + right) >> 1;
mergeSortCore(nums, left, mid, temp);
mergeSortCore(nums, mid + 1, right, temp);
// 两个一半的数组归并完成之后, 保存nums数组的[left, right]部分到temp作为归并的辅助数组
for (int i = left; i <= right; i++) {
temp[i] = nums[i];
}
// 接下来对两部分已经排序的数组做归并
int aPtr = left, bPtr = mid + 1;
int cursor = left;
while (aPtr <= mid && bPtr <= right) {
if (temp[aPtr] <= temp[bPtr]) {
nums[cursor++] = temp[aPtr++];
} else {
nums[cursor++] = temp[bPtr++];
}
}
// 其中一个数组已经归并完成, 将另一个数组的未归并部分直接拷贝
if (aPtr > mid) {
System.arraycopy(temp, bPtr, nums, cursor, right - bPtr + 1);
} else {
System.arraycopy(temp, aPtr, nums, cursor, mid - aPtr + 1);
}
}
在归并排序的基础上加上对于逆序对的计算, 代码如下
public int reversePairs(int[] nums) {
int l = 0, r = nums.length - 1;
int[] copy = Arrays.copyOf(nums, nums.length);
int[] temp = new int[nums.length];
int res = mergeSortCore(copy, 0, nums.length - 1, temp);
return res;
}
public int mergeSortCore(int[] nums, int left, int right, int[] temp) {
if (left >= right) {
return 0;
}
// 先将数组切分成两半, 递归的归并这两个一半的数组
int mid = (left + right) >> 1;
int leftPairs = mergeSortCore(nums, left, mid, temp);
int rightPairs = mergeSortCore(nums, mid + 1, right, temp);
// 两个一半的数组归并完成之后, 保存nums数组的[left, right]部分到temp作为归并的辅助数组
for (int i = left; i <= right; i++) {
temp[i] = nums[i];
}
int crossPairs = 0;
// 接下来对两部分已经排序的数组做归并
int aPtr = left, bPtr = mid + 1;
int cursor = left;
while (aPtr <= mid && bPtr <= right) {
if (temp[aPtr] <= temp[bPtr]) {
nums[cursor++] = temp[aPtr++];
} else {
// aPtr指针值大于bPtr的值
nums[cursor++] = temp[bPtr++];
// bPtr指针值 与 当前 aPtr之后的所有值构成逆序对
crossPairs += (mid - aPtr + 1);
}
}
// 其中一个数组已经归并完成, 将另一个数组的未归并部分直接拷贝
if (aPtr > mid) {
System.arraycopy(temp, bPtr, nums, cursor, right - bPtr + 1);
} else {
System.arraycopy(temp, aPtr, nums, cursor, mid - aPtr + 1);
}
return leftPairs + rightPairs + crossPairs;
}
归并排序还有一种写的方法, 代码如下
public int reversePairs(int[] nums) {
int len = nums.length;
// 如果没有数或者只有1个数字, 直接返回0
if (len < 2) {
return 0;
}
// copy 只是为了防止原数组被修改, 所以拷贝一个副本
int[] copy = Arrays.copyOf(nums, len);
// temp 是归并排序的辅助数组
int[] temp = new int[len];
return reversePairs(copy, 0, len-1, temp);
}
// 计算 [left, right] 的逆序对个数并且排序
public int reversePairs(int[] nums, int left, int right, int[] temp) {
if (left == right) {
return 0;
}
int mid = left + ((right - left) >> 1);
// 递归左半边归并排序, 并且计算左半边的逆序对
int leftPairs = reversePairs(nums, left, mid, temp);
// 递归右半边归并排序, 并且计算右半边的逆序对
int rightPairs = reversePairs(nums, mid + 1, right, temp);
// 优化 : 两边已经排好序时, 并且整个数组都已经有序时, 就不用再继续进行归并了
if (nums[mid] <= nums[mid+1]) {
return leftPairs + rightPairs;
}
// 归并左右的两个半边的数组, 并计算跨这个半边的逆序对的个数
int crossPairs = mergeAndCount(nums, left, mid , right, temp);
// 逆序对总数是左半边逆序对的个数 + 右半边逆序对个数 + 跨越两个半边的逆序对总和。
return leftPairs + rightPairs + crossPairs;
}
// 归并排序的具体过程
public int mergeAndCount(int[] nums, int left, int mid, int right, int[] temp) {
// temp 是对 [left, mid] [mid + 1, right] 两个有序数组进行归并排序的辅助数组
for (int i = left; i <= right; i++) {
temp[i] = nums[i];
}
int i = left, j = mid + 1;
int count = 0;
for (int k = left; k <= right; k++) {
if (i == mid + 1) {
// 左边已经全部归并完成
nums[k] = temp[j++];
} else if (j == right + 1) {
// 右边全部归并完成
nums[k] = temp[i++];
}
// 这里只有<= 归并排序才是一个稳定的排序
else if (temp[i] <= temp[j]) {
nums[k] = temp[i++];
} else {
nums[k] = temp[j++];
// 逆序对是左边还没有归并的数
count += (mid - i + 1);
}
}
return count;
}


