HDU - 6440（费马小定理）

链接：HDU - 6440

题意：重新定义加法和乘法，使得 (m+n)^p = m^p + n^p 成立，p是素数。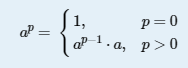，且satisfied that there exists an integer q(0<q<p) to make the set {q^k|0<k<p,k∈Z} equal to {k|0<k<p,k∈Z}。

题解：

#include <bits/stdc++.h>
using namespace std;

const double EPS = 1e-6;
const int INF = 0x3f3f3f3f;
const int mod = 1e9 + 7;
const int maxn = 1e5 + 10;
int p;

int main()
{
    int T;
    scanf("%d", &T);
    while(T--){
        scanf("%d", &p);
        for(int i = 0; i < p; i++){
            for(int j = 0; j < p; j++){
                printf("%d%c", (i + j) % p, j == p - 1 ? '\n' : ' ');
            }
        }
        for(int i = 0; i < p; i++){
            for(int j = 0; j < p; j++){
                printf("%d%c", (i * j) % p, j == p - 1 ? '\n' : ' ');
            }
        }
    }

    return 0;
}