树的基本概念

树：

• 树是一种递归数据结构，包含一个或多个数据节点的集合，其中一个节点被指定为树的根节点，而其余节点被称为根的子节点。
• 除根节点以外的其他节点均被划分为多个非空集，其中每个空集都称为子树。
• 树的节点或者在它们之间保持父子关系，或者它们是姐妹节点。
• 在一般树中，一个节点可以有任意数量的子节点，但只能有一个父节点。
• 下图显示了一棵树，其中节点A是树的根节点，而其他节点可以看作是A的孩子。

 

 

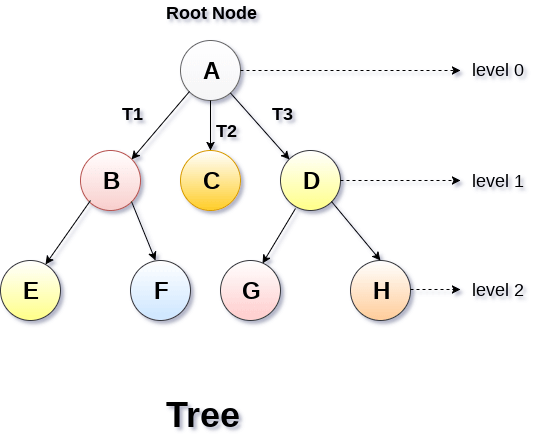
基本术语

• 根节点：-根节点是树层次结构中的最高节点。换句话说，根节点是没有任何父节点的节点。
• 子树：-如果根节点不为空，则树T1，T2和T3被称为根节点的子树。
• 叶子节点：-没有任何子节点的树的节点称为叶子节点。叶节点是树的最底部节点。普通树中可以有任意数量的叶节点。叶节点也可以称为外部节点。
• 程度：-节点的程度等于节点具有的子代数。在上图所示的树中，节点B的度为2。叶节点的度始终为0，而​​在完整的二叉树中，每个节点的度均等于2。

二叉树：

每个节点最多有2个节点的树；

二叉树的类型

1.严格二叉树

每个非叶节点都包含非空的左右子树

 

 

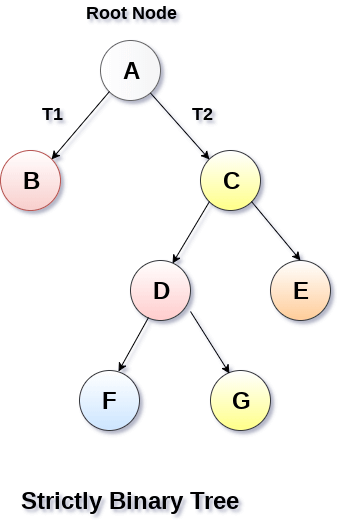
2.满二叉树（特殊的完全二叉树）

所有的叶子节点都位于同一级。

 

 

 

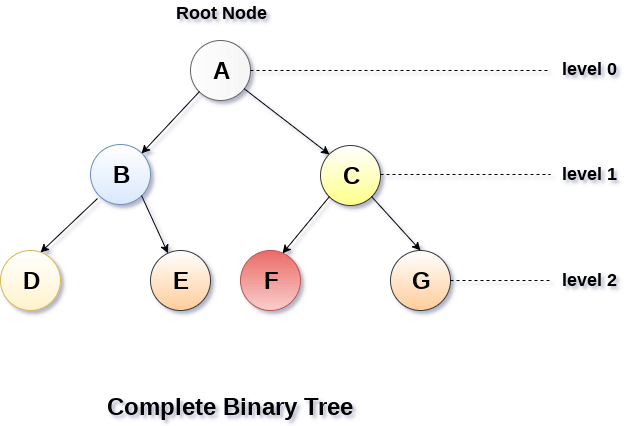
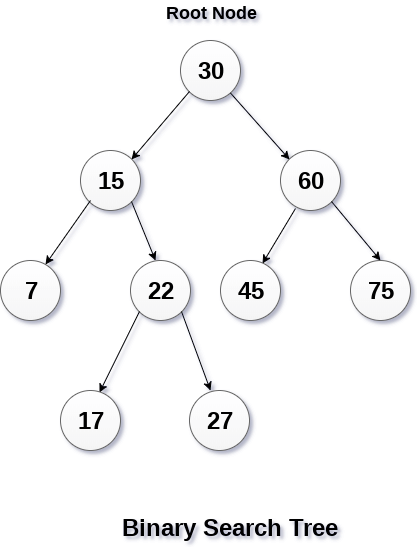
二叉排序树：

二叉树的基础上满足如下特性则为二叉排序树；

• 若它的左子树不为空，则左子树的所有节点的值均小于它的根节点。
• 若它的右子树不为空，则右子树的所有节点的值均大于它的根节点。
• 它的左右子树也分别为二叉排序树。

 

 优点：

1. 在二叉搜索树中搜索变得非常有效，因为我们在每一步都得到了提示，即哪个子树包含所需的元素。
2. 与数组和链表相比，二进制搜索树被认为是有效的数据结构。在搜索过程中，它会在每个步骤中删除一半的子树。在二叉搜索树中搜索元素需要o（log ₂ n）时间。在最坏的情况下，搜索元素所需的时间为0（n）。
3. 与数组和链表中的插入和删除操作相比，它还加快了插入和删除操作的速度。

 

二叉平衡树（AVL）：

所有节点的左右子树的高度差小于1的二叉排序树；

 

 

B树：

Ｂ树出现是因为磁盘ＩＯ。ＩＯ操作的效率很低，那么，当在大量数据存储中，查询时我们不能一下子将所有数据加载到内存中，只能逐一加载磁盘页，每个磁盘页对应树的节点。造成大量磁盘ＩＯ操作（最坏情况下为树的高度）。平衡二叉树由于树深度过大而造成磁盘IO读写过于频繁，进而导致效率低下。
　　所以，我们为了减少磁盘ＩＯ的次数，就你必须降低树的深度，将“瘦高”的树变得“矮胖”。

 

B 树又叫平衡多路查找树。一棵m阶的B 树 (m叉树)的特性如下：

1. 根节点必须至少含有2个节点。
2. 除了根节点和叶节点之外，B树中的每个节点至少包含m / 2个子节点。
3. B树中的每个节点最多包含m个子节点
4. 所有叶节点必须处于同一级别。

下图显示了4阶AB树。

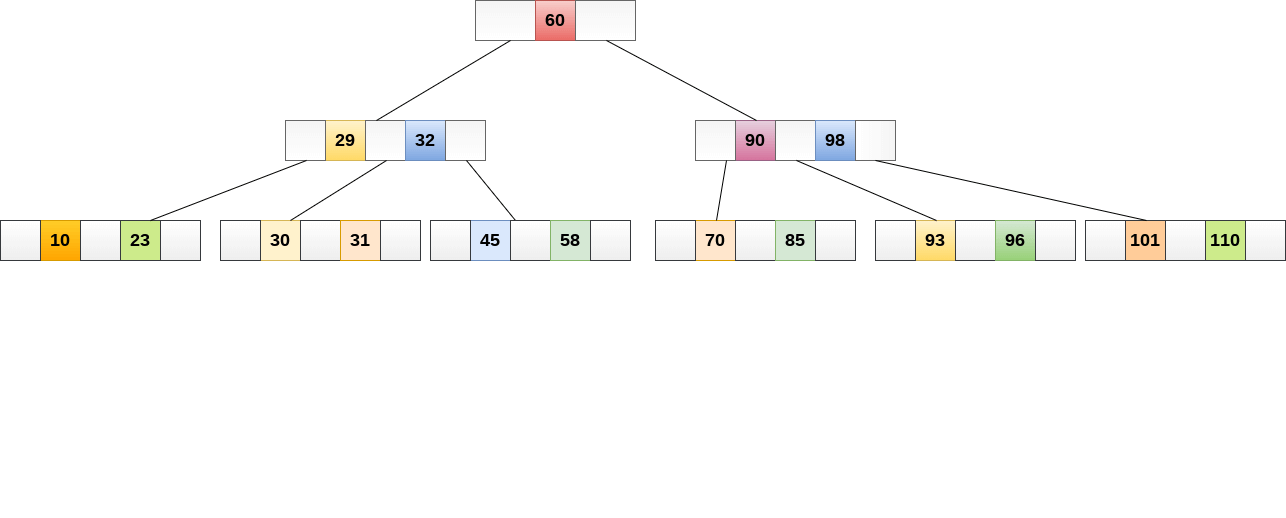
B+树：

B +树是B树的扩展，它允许有效的插入，删除和搜索操作。

在B树中，键和记录都可以存储在内部节点和叶节点中。而在B +树中，记录（数据）只能存储在叶节点上，而内部节点只能存储键值。

B +树的叶节点以单链接列表的形式链接在一起，以使搜索查询更高效。

B +树用于存储无法存储在主存储器中的大量数据。由于总是限制主存储器的大小，因此B +树的内部节点（访问记录的键）存储在主存储器中，而叶节点存储在辅助存储器中。

B +树的内部节点通常称为索引节点。下图显示了3级的B +树。

 

 

 

 

B +树的优势

1. 可以以相同数量的磁盘访问来获取记录。
2. 与B树相比，树的高度保持平衡并且较小。
3. 我们可以依次或直接访问存储在B +树中的数据。
4. 键用于索引。
5. 由于数据仅存储在叶节点上，因此搜索查询速度更快。

B树VS B +树

SN	B树	B +树
1个	搜索键不能重复存储。	可能存在冗余搜索键。
2	数据可以存储在叶节点以及内部节点中	数据只能存储在叶节点上。
3	搜索一些数据的过程较慢，因为可以在内部节点以及叶节点上找到数据。	由于只能在叶节点上找到数据，因此搜索相对较快。
4	内部节点的删除是如此复杂且耗时。	删除绝不会是一个复杂的过程，因为元素总是会从叶节点中删除。
5	叶节点不能链接在一起。	叶节点链接在一起，使搜索操作更高效。

 

 

红黑树：

 红黑树是一棵二叉搜索树，它在每个节点上增加了一个存储位来表示节点的颜色，可以是Red或Black。

通过对任意一条从根到叶子的简单路径上各个节点的颜色进行约束，红黑树确保没有一条路径会比其他路径长出2倍，因而是近似平衡的。

特性：

1. 每个节点要么是红色，要么是黑色。
2. 根节点是黑色。
3. 叶子节点是黑色。
4. 相邻的两个节点不能同时位红色。
5. 任意节点到其所有后代叶子节点的路径上，都包含相同数目的黑色节点。
6. 插入的节点一定是红色。

 

 

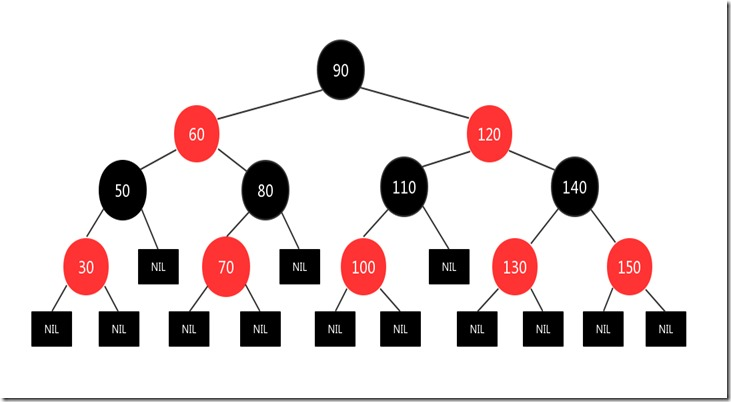
 从某个节点x出发（不含该节点）到达一个叶节点的任意一条简单路径上的黑色节点个数成为该节点的黑高；

 

 （以上如有错误或理解不到位地方欢迎指正）

参考资料：

• 算法导论
• https://www.javatpoint.com/tree