各种相似度计算的python实现

各种相似度计算的python实现

 

前言

在数据挖掘中有很多地方要计算相似度，比如聚类分析和协同过滤。计算相似度的有许多方法，其中有欧几里德距离、曼哈顿距离、Jaccard系数和皮尔逊相关度等等。我们这里把一些常用的相似度计算方法，用python进行实现以下。如果是初学者，我认为把公式先写下来，然后再写代码去实现比较好。 

欧几里德距离

几个数据集之间的相似度一般是基于每对对象间的距离计算。最常用的当然是欧几里德距离，其公式为:

#-*-coding:utf-8 -*-

#计算欧几里德距离：
def euclidean(p,q):
#如果两数据集数目不同，计算两者之间都对应有的数
same = 0
for i in p:
    if i in q:
        same +=1

#计算欧几里德距离,并将其标准化
e = sum([(p[i] - q[i])**2 for i in range(same)])
return 1/(1+e**.5)

 

我们用数据集可以去算一下： 

p = [1,3,2,3,4,3]
q = [1,3,4,3,2,3,4,3]
print euclidean(p,q)

 

得出结果是：0.261203874964

皮尔逊相关度

几个数据集中出现异常值的时候，欧几里德距离就不如皮尔逊相关度‘稳定’，它会在出现偏差时倾向于给出更好的结果。其公式为：

 

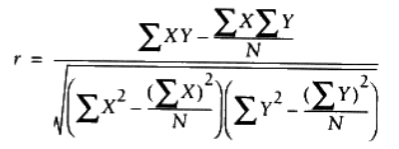
-*-coding:utf-8 -*-

#计算皮尔逊相关度：
def pearson(p,q):
#只计算两者共同有的
    same = 0
    for i in p:
        if i in q:
            same +=1

    n = same
    #分别求p，q的和
    sumx = sum([p[i] for i in range(n)])
    sumy = sum([q[i] for i in range(n)])
    #分别求出p，q的平方和
    sumxsq = sum([p[i]**2 for i in range(n)])
    sumysq = sum([q[i]**2 for i in range(n)])
    #求出p，q的乘积和
    sumxy = sum([p[i]*q[i] for i in range(n)])
    # print sumxy
    #求出pearson相关系数
    up = sumxy - sumx*sumy/n
    down = ((sumxsq - pow(sumxsq,2)/n)*(sumysq - pow(sumysq,2)/n))**.5
    #若down为零则不能计算，return 0
    if down == 0 :return 0
    r = up/down
    return r

用同样的数据集去计算：

p = [1,3,2,3,4,3]
q = [1,3,4,3,2,3,4,3]
print pearson(p,q)

得出结果是：0.00595238095238

曼哈顿距离

曼哈顿距离是另一种相似度计算方法，不是经常需要，但是我们仍然学会如何用python去实现，其公式为：

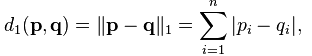
#-*-coding:utf-8 -*-

#计算曼哈顿距离：
def manhattan(p,q):
#只计算两者共同有的
    same = 0
    for i in p:
        if i in q:
        same += 1
#计算曼哈顿距离
    n = same
    vals = range(n)
    distance = sum(abs(p[i] - q[i]) for i in vals)
    return distance

用以上的数据集去计算：

p = [1,3,2,3,4,3]
q = [1,3,4,3,2,3,4,3]
print manhattan(p,q)

得出结果为4

Jaccard系数

当数据集为二元变量时，我们只有两种状态：0或者1。这个时候以上的计算相似度的方法就无法派上用场，于是我们引出Jaccard系数，这是一个能够表示两个数据集都是二元变量（也可以多元）的相似度的指标，其公式为：

#-*-coding:utf-8 -*-

# 计算jaccard系数
def jaccard(p,q):
    c = [a for i in p if v in b]
    return float(len(c))/(len(a)+len(b)-len(b))
#注意：在使用之前必须对两个数据集进行去重

我们用一些特殊的数据集去测试一下：

p = ['shirt','shoes','pants','socks']
q = ['shirt','shoes']
print jaccard(p,q)

得出结果是:0.5

Tanimoto系数

Tanimoto系数是一种度量两个集合之间相似程度的方法（与Jaccard 系数相似，但不是完全相同）。其主要用于二元变量或者多元变量之间的数据集之间的相似度计算，其公式为：

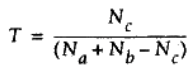
#-*-coding:utf-8-*-
def tanimoto(p,q):
    c = [v for v in p if v in q]
    return float(len(c) / (len(a) + len(b) - len(c)))

当比较的数据集的数据集合中的元素都是相异的时候，Jaccard系数与Tanimoto系数相同。

 

参考：《集体智慧编程》

　　　《数据挖掘：概念与技术》