SSL/TLS协议运行机制
SSL/TLS协议运行机制
引言
SSL (Secure Socket Layer) /TLS (Transport Layer Security) 协议一般工作在TCP层(4层)和各种应用层(7层)之间,例如HTTP、mysql 都可以使用SSL/TLS进行安全连接。

SSL/TLS协议发展历史:
- 1994年,NetScape公司设计了SSL协议(Secure Sockets Layer)的1.0版,但是未发布。
- 1995年,NetScape公司发布SSL 2.0版,很快发现有严重漏洞。
- 1996年,SSL 3.0版问世,得到大规模应用。
- 1999年,互联网标准化组织ISOC接替NetScape公司,发布了SSL的升级版TLS 1.0版(也称为SSL3.1)。
- 2006年和2008年,TLS进行了两次升级,分别为TLS 1.1版(或SSL3.2)和TLS 1.2版(或SSL3.3);
- 2011年TLS 1.2的修订版;——主流
- 2018年,TSL1.3版本发布,目前支持的浏览器可能未普及。
加密算法
以下加密算法涉及到python实现依赖:
pip install pycryptodome
pip install pyDH
对称加密算法
- 甲方选择某一种加密规则,对信息进行加密;
- 乙方使用同一种规则,对信息进行解密。
这种加密模式有一个最大弱点:甲方必须把加密规则告诉乙方,否则无法解密。保存和传递密钥,就成了最头疼的问题。
Python中 DES 的用法
#!/usr/bin/env python from Crypto import Random from Crypto.Hash import SHA from Crypto.Cipher import DES from Crypto.Cipher import PKCS1_v1_5 as Cipher_pkcs1_v1_5 from Crypto.Signature import PKCS1_v1_5 as Signature_pkcs1_v1_5 from Crypto.PublicKey import RSA import base64 key = '12345678' raw = 'meitu company11111111111111111111' pad = 8 - len(raw) % 8 pad_str = '' for i in range(pad): pad_str += chr(pad) cipher = DES.new(key, DES.MODE_ECB) data = cipher.encrypt(raw + pad_str) print "encrypted text: %s\n"%(data) cipher = DES.new(key, DES.MODE_ECB) print "decrypted text: %s\n"%(cipher.decrypt(data))
Python中 AES 的用法
#!/usr/bin/env python from Crypto import Random from Crypto.Hash import SHA from Crypto.Cipher import AES from Crypto.Cipher import PKCS1_v1_5 as Cipher_pkcs1_v1_5 from Crypto.Signature import PKCS1_v1_5 as Signature_pkcs1_v1_5 from Crypto.PublicKey import RSA import base64 key = 'chenqichenqi1234' raw = 'meitu company11111111111111111111' iv = Random.new().read(AES.block_size) cipher = AES.new(key, AES.MODE_CFB, iv) data = iv + cipher.encrypt(raw) print "encrypted text: %s\n"%(data[16:]) iv = data[:16] cipher = AES.new(key, AES.MODE_CFB, iv) print "decrypted text: %s\n"%(cipher.decrypt(data[16:]))
运行结果
encrypted text: nl"MX\#
decrypted text: meitu company11111111111111111111
公钥加密算法
- 乙方生成两把密钥(公钥和私钥),公钥是公开的,任何人都可以获得,私钥则是保密的;
- 甲方获取乙方的公钥,然后用它对信息加密;
- 乙方得到加密后的信息,用私钥解密。
通过公钥加密的信息只有私钥解得开,那么只要私钥不泄漏,通信就是安全的。
1976年,两位美国计算机学家Whitfield Diffie 和 Martin Hellman,提出了一种崭新构思,可以在不直接传递密钥的情况下,完成解密。这被称为"Diffie-Hellman密钥交换算法"。
1977年,三位数学家Rivest、Shamir 和 Adleman 设计了一种算法,可以实现非对称加密。这种算法用他们三个人的名字命名,叫做RSA算法,RSA广泛应用在SSH、SSL/TLS等协议中。
Python 中 DH 的用法
#!/usr/bin/python import pyDH d1 = pyDH.DiffieHellman() d1_pubkey = d1.gen_public_key() d2 = pyDH.DiffieHellman() d2_pubkey = d2.gen_public_key() d1_sharedkey = d1.gen_shared_key(d2_pubkey) d2_sharedkey = d2.gen_shared_key(d1_pubkey) print d1_sharedkey == d2_sharedkey print "sharedkey: %s"%d1_sharedkey
DH 的数学原理
DH算法的有效性依赖于计算离散对数的难度。
简言之,可以如下定义离散对数:首先定义一个质数p的原根,为其各次幂产生从1 到p-1的所有整数根,也就是说,如果g是质数p的一个原根,那么数值
g mod p, g2 mod p, ..., gp-1 mod p
是各不相同的整数,并且以某种排列方式组成了从1到p-1的所有整数。
对于一个整数b和质数p的一个原根g,可以找到惟一的指数i,使得
b = gi mod p 其中0 ≤ i ≤ (p-1)
指数 i 称为b的以g为基数的模p的离散对数或者指数。该值被记为indg ,p(b)。
如下图,有两个全局公开的参数,一个质数p和一个整数g,g是p的一个原根。
服务端的私钥和公钥分别是a和A,客户端的私钥和公钥分别是b和B;
服务端根据a、p、g,可以计算出公钥A;
服务端将g, p, A明文传送给客户端,客户端可以计算自己的公钥B,以及共享密钥K;
客户端将B明文发送给服务端,服务端也可以计算出共享密钥K。

Python中 RSA 的用法
#!/usr/bin/env python from Crypto import Random from Crypto.Hash import SHA from Crypto.Cipher import AES from Crypto.Cipher import PKCS1_v1_5 as Cipher_pkcs1_v1_5 from Crypto.Signature import PKCS1_v1_5 as Signature_pkcs1_v1_5 from Crypto.PublicKey import RSA import base64 random_generator = Random.new().read rsa = RSA.generate(1024, random_generator) # generate key pair private_pem = rsa.exportKey() public_pem = rsa.publickey().exportKey() # encrypted message = "meitu company" rsakey = RSA.importKey(public_pem) cipher = Cipher_pkcs1_v1_5.new(rsakey) cipher_text = base64.b64encode(cipher.encrypt(message)) print cipher_text # decrypted rsakey = RSA.importKey(private_pem) cipher = Cipher_pkcs1_v1_5.new(rsakey) text = cipher.decrypt(base64.b64decode(cipher_text), random_generator) print text
如果我们将RSA算法运用到C/S架构网络通信中的话,如果Client要向Server发送一段消息:
- Server事先生成秘钥对;
- Client请求Server的公钥;
- Client用公钥加密mesage,并将密文发给Server;
- Server用私钥解密,获取明文;
如果Server要向Client发送消息,流程也是类似的。
这里其实还有个问题,Server的公钥是公开的,任何人都可以得到。Server只能保证只有自己的私钥可以解密消息,但不能识别消息的来源是不是可靠,因为任何人都可能用公钥加密一段文本发给Server,这里就涉及到数字签名。
数字签名
对数据加密必须要是可逆的,如果不能解密,那对要传输的信息就失去了意义。而签名不需要可逆,签名是为了证明信息没有被篡改,例如我们对要传输的数据使用MD5或SHA256算法计算hash值,在信息的接收方对收到的数据同样使用M5D/SHA256计算hash值,然后与发送方的hash值比对,就知道信息是否失真。因为这里hash计算可以保证不同的内容一定会得到不同的hash值,所以只要内容一被修改,根据信息内容计算的hash值就会变化。
当然,不怀好意的人也可以修改信息内容的同时也修改hash值,从而让它们可以相匹配,为了防止这种情况,hash值一般都会加密后再和信息一起发送,以保证这个hash值不被修改。至于如何让别人可以解密这个签名,这个过程涉及到数字证书等概念,我们后面在说到数字证书时再详细说明,这里您先只需先理解签名的这个概念。
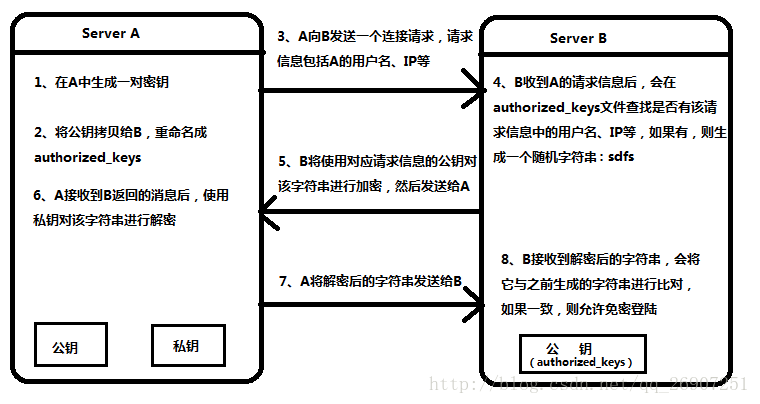
SSH免密登录
SSH免密登录是非对称加密的一个应用场景。
像gitlab支持ssh免密登录,通常是需要用户事先上传自己的公钥:
RSA 的数学原理
如上面的应用知道RSA特性:
- 公钥加密,私钥可以解密;
- 私钥签名,公钥可以验证;
那么要如何生成一对密钥呢?
- 随机选择两个不相等的质数p和q,例如 p=61, q=53;
- n = p * q即为密钥,这里n = 61 *53 = 3233,其二进制为110010100001,一共12位,这个就是密钥的长度,实际应用中,RSA密钥一般是1024位,重要场合则为2048位。
- 计算欧拉函数 φ(n) = (p-1)*(q-1)= 60 *52= 3120;
- 选出一个随机数e,满足 1< e < φ(n),且e与φ(n) 互质,这里在1到3120之间,随机选择了e=17;
- 计算e对于φ(n)的模反元素d,d要满足 ed ≡ 1 (mod φ(n)),这个式子等价于ed - 1 = kφ(n),将e=17, φ(n) =3120代入,利用扩展欧几里得算法得到d=2753, k=-15;
- 将n和e封装成公钥(3233, 17),n和d封装成私钥(3233, 2753)。
- 用公钥(n, e)对m加密,me ≡ c (mod n),所谓加密,即计算出c,也即加密后的数据,若m=65,则c = 6517 % 3233 =2790;
- 用私钥(n, d)对c解密,cd ≡ m (mod n),m = 27902753 % 3233 = 65;
上面第7、8步如果把公私钥对调,也仍成立,这就是签名的数学意义。
从上面的公、私钥生成过程看,公钥包含n、e,私钥包含n、d,那么,有无可能在已知n和e的情况下,推导出d呢,如果能的话就能破解私钥:
- ed≡1 (mod φ(n)),要计算出d,需要知道e和φ(n),而e在公钥中,所以要求φ(n);
- φ(n)=(p-1)(q-1),只有知道p和q,才能算出φ(n);
- n=pq。只有将n因数分解,才能算出p和q。
可见,如果n可以被因数分解,d就可以算出,也就意味着私钥被破解。
举例来说,你可以对3233进行因数分解(61×53),但是你没法对下面这个整数进行因数分解:
12301866845301177551304949
58384962720772853569595334
79219732245215172640050726
36575187452021997864693899
56474942774063845925192557
32630345373154826850791702
61221429134616704292143116
02221240479274737794080665
351419597459856902143413 =
33478071698956898786044169
84821269081770479498371376
85689124313889828837938780
02287614711652531743087737
814467999489
×
36746043666799590428244633
79962795263227915816434308
76426760322838157396665112
79233373417143396810270092
798736308917
目前已知被破解的最长RSA密钥就是768位。
PS,上述推演中用到的一些数学概念:
- 如果两个正整数,除了1以外,没有其他公因子,我们就称这两个数是互质关系(coprime)。比如,15和32没有公因子,所以它们是互质关系。
- 欧拉函数:任意给定正整数n,请问在小于等于n的正整数之中,有多少个与n构成互质关系?(比如,在1到8之中,有多少个数与8构成互质关系?1, 3, 5, 7,那么φ(8)=4)
- 欧拉定理:如果两个正整数a和n互质,则n的欧拉函数 φ(n) 可以让下面的等式成立:(aφ(n) ) % n = 1,记为 aφ(n) ≡ 1(mod n)
- 模反元素:如果两个正整数a和n互质,那么一定可以找到整数b,使得 ab % n = 1,b即为a的模反元素,记为 ab ≡ 1(mod n);
SSL/TLS 协议
四次握手
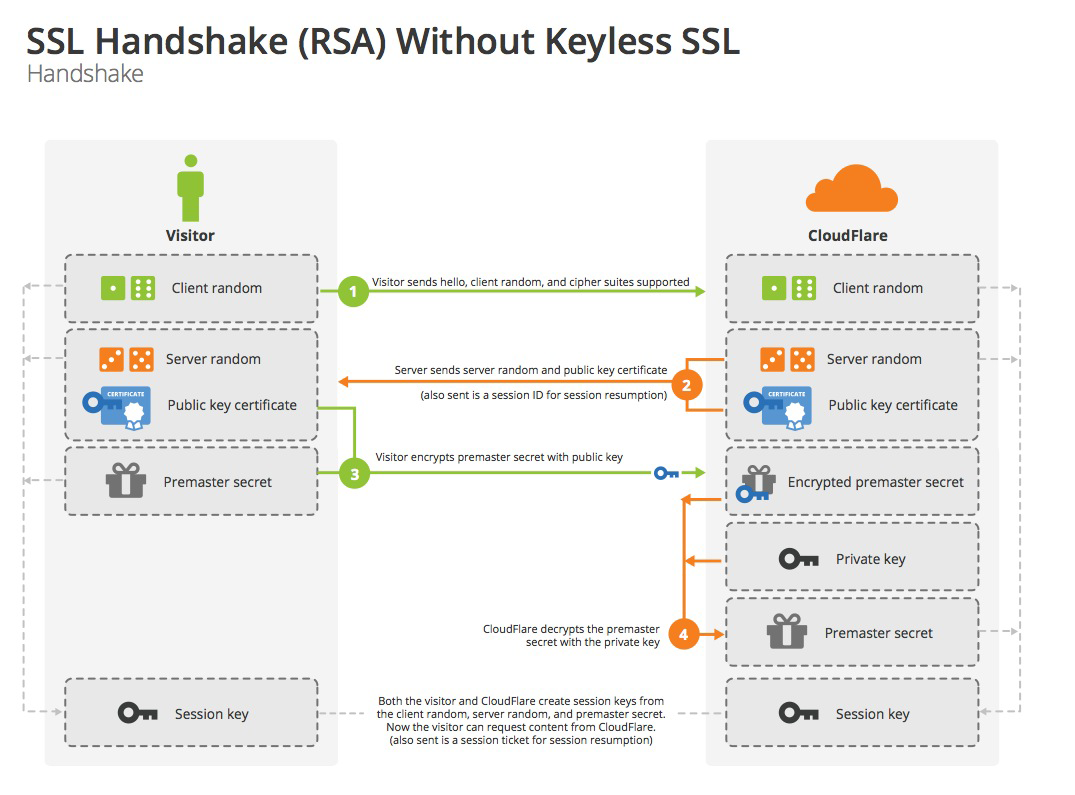
如下图:
ClientHello
首先,客户端(通常是浏览器)先向服务器发出加密通信的请求,这被叫做ClientHello请求。
在这一步,客户端主要向服务器提供以下信息。
- 支持的协议版本,比如TLS 1.2版;
- 一个客户端生成的随机数,稍后用于生成"对话密钥"
- 支持的加密方法,比如RSA公钥加密
- 支持的压缩方法;
这里需要注意的是,客户端发送的信息之中不包括服务器的域名。也就是说,理论上服务器只能包含一个网站,否则会分不清应该向客户端提供哪一个网站的数字证书。这就是为什么通常一台服务器只能有一张数字证书的原因。
SeverHello
- 确认使用的加密通信协议版本,比如TLS 1.0版本。如果浏览器与服务器支持的版本不一致,服务器关闭加密通信。
- 一个服务器生成的随机数,稍后用于生成"对话密钥"。
- 确认使用的加密方法,比如RSA公钥加密。
- 服务器证书(包括服务器公钥)。
除了上面这些信息,如果服务器需要确认客户端的身份,就会再包含一项请求,要求客户端提供"客户端证书"。比如,金融机构往往只允许认证客户连入自己的网络,就会向正式客户提供USB密钥,里面就包含了一张客户端证书。
Client Key Exchange
客户端收到服务器回应以后,首先验证服务器证书。如果证书不是可信机构颁布、或者证书中的域名与实际域名不一致、或者证书已经过期,就会向访问者显示一个警告,由其选择是否还要继续通信。
如果证书没有问题,客户端就会从证书中取出服务器的公钥。然后,向服务器发送下面三项信息。
- 生成一个随机数(pre-master key),并对该随机数用服务器公钥加密,防止被窃听。
- 编码改变通知,表示随后的信息都将用双方商定的加密方法和密钥发送。
- 客户端握手结束通知,表示客户端的握手阶段已经结束。这一项同时也是前面发送的所有内容的hash值,用来供服务器校验。
上面第一项的随机数,是整个握手阶段出现的第三个随机数,有了它以后,客户端和服务器就同时有了三个随机数,接着双方就用事先商定的加密方法,各自生成本次会话所用的同一把"会话密钥"。
至于为什么一定要用三个随机数,来生成"会话密钥",解释如下:
"不管是客户端还是服务器,都需要随机数,这样生成的密钥才不会每次都一样。由于SSL协议中证书是静态的,因此十分有必要引入一种随机因素来保证协商出来的密钥的随机性。
对于RSA密钥交换算法来说,pre-master-key本身就是一个随机数,再加上hello消息中的随机,三个随机数通过一个密钥导出器最终导出一个对称密钥。
pre master的存在在于SSL协议不信任每个主机都能产生完全随机的随机数,如果随机数不随机,那么pre master secret就有可能被猜出来,那么仅适用pre master secret作为密钥就不合适了,因此必须引入新的随机因素,那么客户端和服务器加上pre master secret三个随机数一同生成的密钥就不容易被猜出了,一个伪随机可能完全不随机,可是是三个伪随机就十分接近随机了,每增加一个自由度,随机性增加的可不是一。"
Finish
服务器收到客户端的第三个随机数pre-master key之后,计算生成本次会话所用的"会话密钥"。然后,向客户端最后发送下面信息。
- 编码改变通知,表示随后的信息都将用双方商定的加密方法和密钥发送。
- 服务器握手结束通知,表示服务器的握手阶段已经结束。这一项同时也是前面发送的所有内容的hash值,用来供客户端校验。
至此,整个握手阶段全部结束。接下来,客户端与服务器进入加密通信,就完全是使用普通的HTTP协议,只不过用"会话密钥"加密内容。
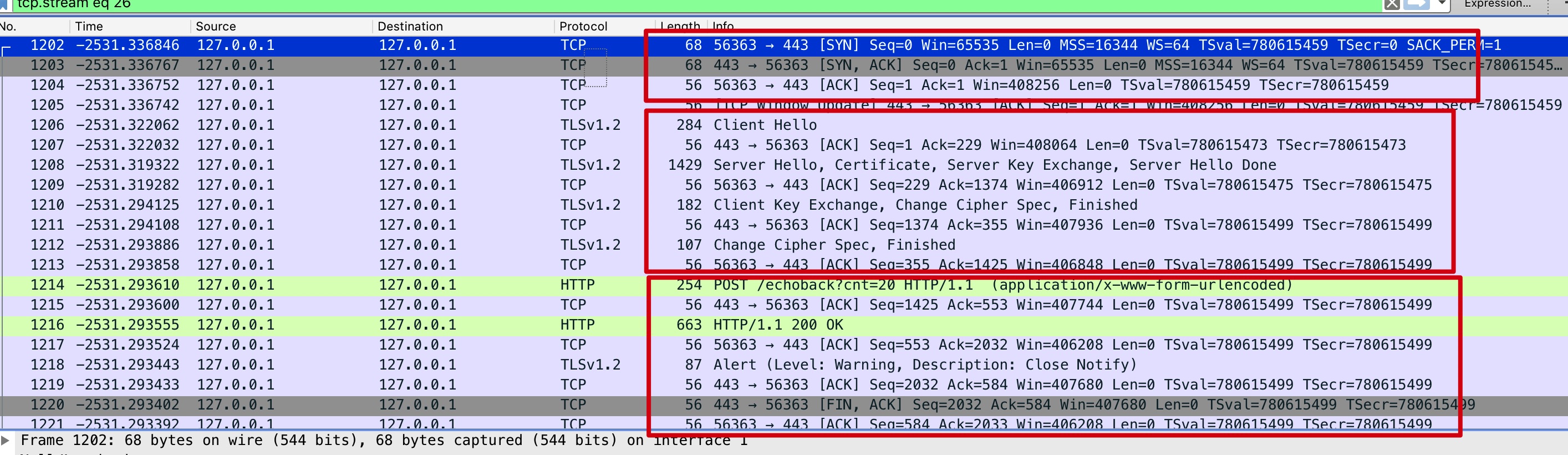
wireshark抓包看下,先是TCP三次握手、然后是SSL四次握手,接着开始HTTP协议数据:
总结下,握手阶段有3点需要注意:
1、生成对话密钥一共需要三个随机数。
2、握手之后的对话使用"对话密钥"加密(对称加密),服务器的公钥和私钥只用于加密和解密"对话密钥"(非对称加密),无其他作用。
3、服务器公钥放在服务器的数字证书之中。
可见,在整个握手阶段都不加密(也没法加密),都是明文的。因此,如果有人窃听通信,他可以知道双方选择的加密方法,以及三个随机数中的两个。整个通话的安全,只取决于第三个随机数(Premaster secret)能不能被破解。
虽然理论上,只要服务器的公钥足够长(比如2048位),那么Premaster secret可以保证不被破解。但是为了足够安全,我们可以考虑把握手阶段的算法从默认的RSA算法,改为 Diffie-Hellman算法。采用DH算法后,Premaster secret不需要传递,双方只要交换各自的参数,就可以算出这个随机数。
session
前面所说的握手阶段用来建立SSL连接,但如果出于某种原因,对话中断了,就需要重新握手。
这时有两种方法可以恢复原来的session:一种叫做session ID,另一种叫做session ticket。
session ID的思想很简单,就是每一次对话都有一个编号(session ID)。如果对话中断,下次重连的时候,只要客户端给出这个编号,且服务器有这个编号的记录,双方就可以重新使用已有的"对话密钥",而不必重新生成一把。
session ID是目前所有浏览器都支持的方法,但是它的缺点在于session ID往往只保留在一台服务器上。所以,如果客户端的请求发到另一台服务器,就无法恢复对话。session ticket就是为了解决这个问题而诞生的,目前只有Firefox和Chrome浏览器支持。
在session ticket的方式中,客户端不再发送session ID,而是发送一个服务器在上一次对话中发送过来的session ticket。这个session ticket是加密的,只有服务器才能解密,其中包括本次对话的主要信息,比如对话密钥和加密方法。当服务器收到session ticket以后,解密后就不必重新生成对话密钥了。
https证书
在SSL/TLS握手中涉及到证书验证的过程,使用openssl命令生成证书的例子:
openssl req -new -newkey rsa:2048 -sha256 -nodes -out example_com.csr -keyout example_com.key -subj "/C=CN/ST=ShenZhen/L=ShenZhen/O=Example Inc./OU=Web Security/CN=example.com"
- C:Country ,单位所在国家,为两位数的国家缩写,如: CN 就是中国
- ST 字段: State/Province ,单位所在州或省
- L 字段: Locality ,单位所在城市 / 或县区
- O 字段: Organization ,此网站的单位名称;
- OU 字段: Organization Unit,下属部门名称;也常常用于显示其他证书相关信息,如证书类型,证书产品名称或身份验证类型或验证内容等;
- CN 字段: Common Name ,网站的域名;
证书生成流程如下:
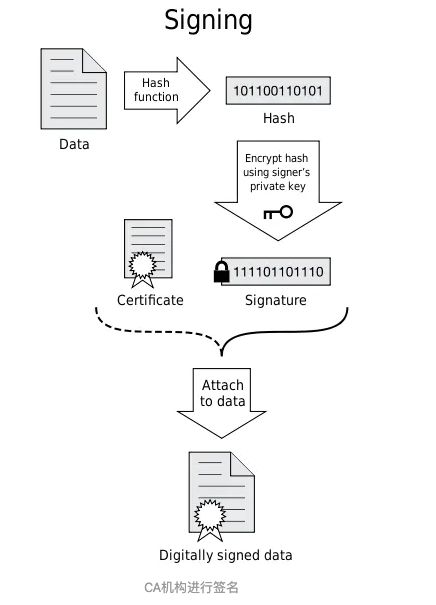
CA机构收到证书申请之后,使用申请中的Hash算法,对部分内容进行摘要,然后使用CA机构自己的私钥对这段摘要信息进行签名.
alpn协议
在google开发的SPDY协议中(HTTP2实验室版本)中,必须基于TLS部署;
虽然后来HTTP/2本身并未要求和HTTPS绑定,但当前的主流浏览器,都只支持基于 HTTPS(TLS) 部署的 HTTP/2。
因此 HTTP/2 应用层协议协商是在 TLS 握手阶段进行的。当浏览器在建立 TLS 连接时,通过 ALPN (Application-Layer Protocol Negotiation) 扩展列出了浏览器支持的各种应用层协议。
如下图,客户端在 Client Hello中声明了alpn扩展,说明其支持http/1.1和http/2两种应用层协议
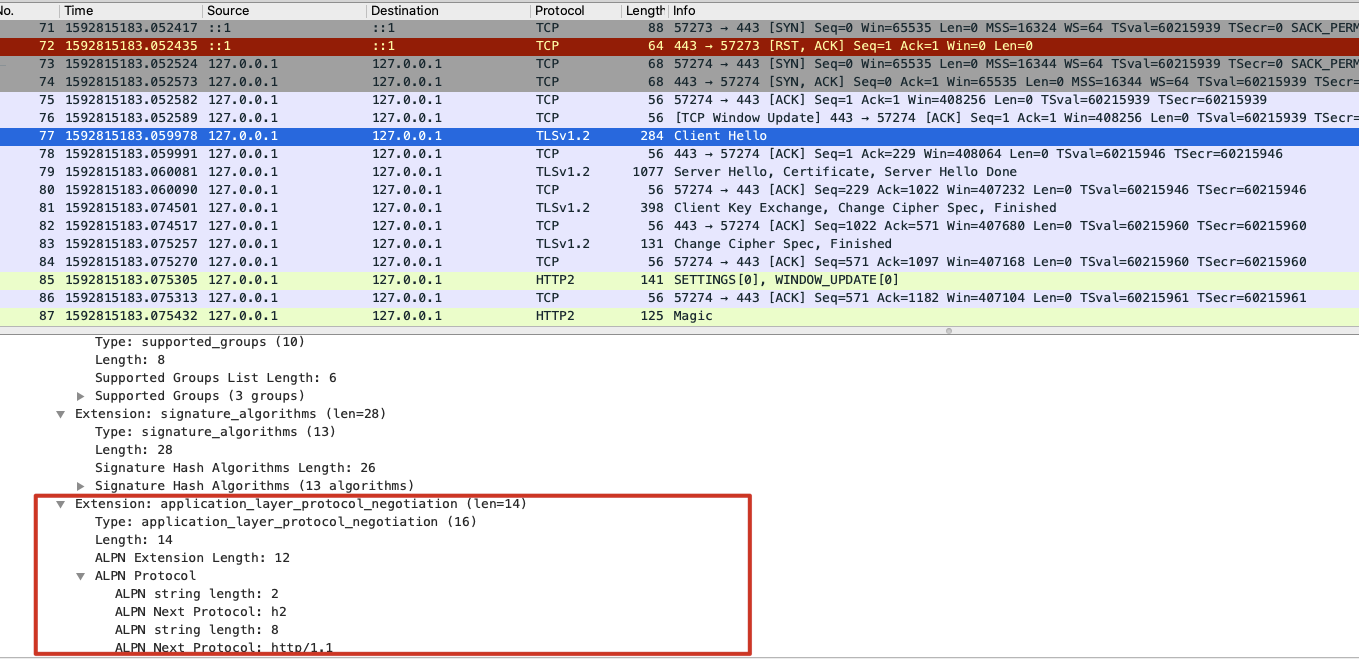
服务器在Server Hello中告诉客户端使用http/2协议。
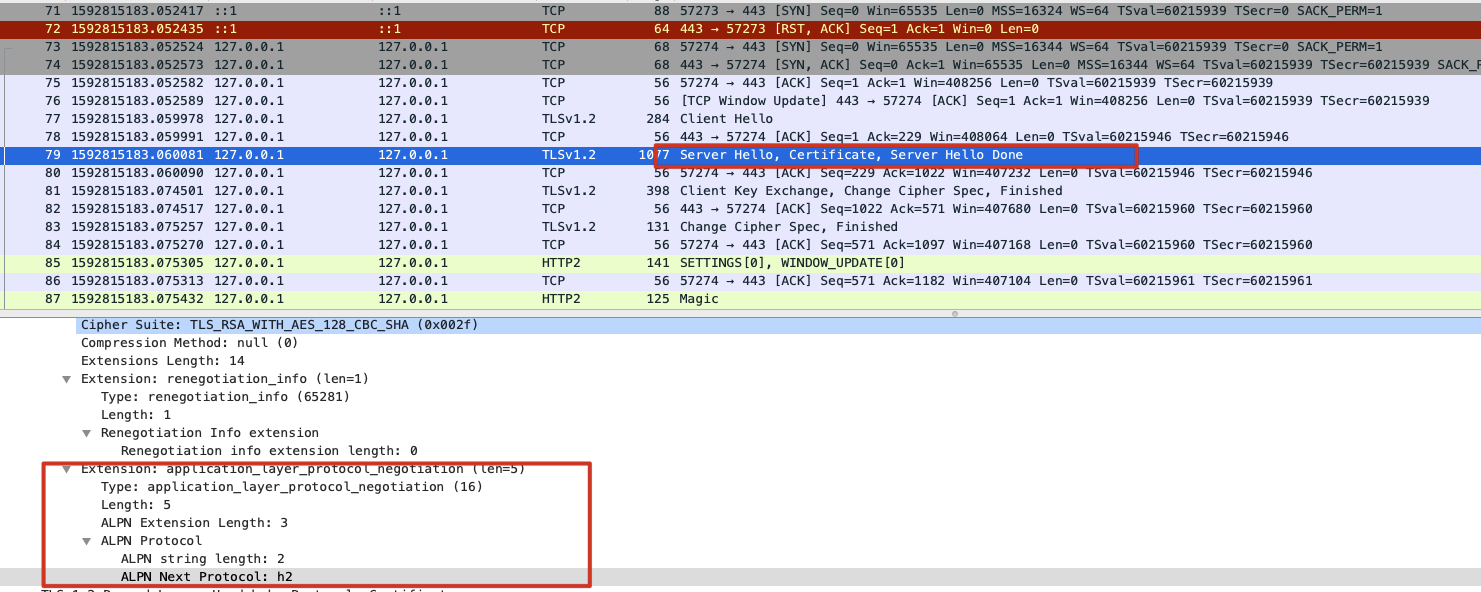
参考文档:
http://www.ruanyifeng.com/blog/2014/09/illustration-ssl.html